Sort summary:
The following figure shows the temporal and spatial complexity of each sorting: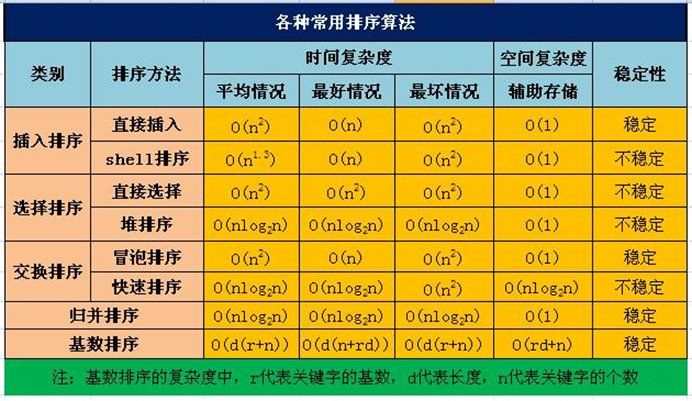

1. Bubble sort:

//Bubble sort
void bubble_sort(vector<int> &v){
	for(int i = 0;i < v.size()-1;i++){//n-1 trip 
		for(int j = 0;j< v.size()-i-1;j++){//n- trips -1 
			if(v[j] > v[j+1]){
				int temp = v[j];
				v[j] = v[j+1];
				v[j+1] = temp;
			}
		}
	}
}

2. Direct insertion sorting:

//Direct insert sort
void insert_sort(vector<int> &v){
	for(int i = 1;i < v.size();i++){
		for(int j = i;j > 0;j--){
			if(v[j] < v[j-1]){
				int temp = v[j];
				v[j] = v[j-1];
				v[j-1] = temp;
			}
		}
	}
} 

1. Hill sort (improved insert sort):

//Shell Sort
void shell_sort(vector<int> &v){
	//Find gap first
	int h = 1;
	while(h < v.size()/3){
		h = h*3 + 1;//Knuth sequence 
	} 
	for(int gap = h;gap > 0;gap = (gap-1)/3){
		//The insertion sort is as follows
		for(int i = gap;i < v.size();i++){
			for(int j = i;j > gap-1;j-=gap){
				if(v[j] < v[j-gap]){
					int temp = v[j];
					v[j] = v[j-gap];
					v[j-gap] = temp;
				}
			}
		} 
	}
}

1. Select sort:

//Selection sort
void select_sort(vector<int> &v){
	for(int i = 0;i < v.size()-1;i++){
		int min = i;
		for(int j = i+1;j < v.size();j++){
			if(v[j] < v[min]){
				min = j;
			}
		}
		if(min != i){
			int temp = v[min];
			v[min] = v[i];
			v[i] = temp;
		}
	}
}

1. Quick sort:

//Partitioning method
int partition(vector<int> &v,int low,int high){
	int mid = low + (high-low)/2;//Pivot on middle element 
	int temp = v[mid];
	v[mid] = v[low];
	v[low] = temp;
	int pivot = v[low];
	while(low < high){
		while(low < high && pivot <= v[high]){
			high--;
		}
		v[low] = v[high];
		while(low < high && v[low] <= pivot){
			low++;
		}
		v[high] = v[low];
	}
	v[low] = pivot;
	return low;
} 
 
//Quick sort 
void quick_sort(vector<int> &v,int low,int high){
	if(low < high){
		int mid = partition(v,low,high);
		quick_sort(v,low,mid-1);
		quick_sort(v,mid+1,high); 
	}
}

1. Merge and sort:

//Merge 
void merge(vector<int> &v,int low,int mid,int high){
	int i = low;
	int j = mid+1;
	int k = 0;
	vector<int> temp;
	temp.resize(high-low+1);
	while(i <= mid && j <= high){
		if(v[i] <= v[j]){
			temp[k++] = v[i++];
		}else{
			temp[k++] = v[j++];
		}
	}
	while(i <= mid){
		temp[k++] = v[i++];
	}
	while(j <= high){
		temp[k++] = v[j++];
	}
	for(int m = 0;m < temp.size();m++){
		v[low+m] = temp[m];
	}
}

//Merge sort
void merge_sort(vector<int> &v,int low,int high){
	if(low < high){
		int mid = low + (high - low) / 2;
		merge_sort(v,low,mid);
		merge_sort(v,mid+1,high);
		merge(v,low,mid,high);
	}
} 

1. Count sort (one of bucket sort):

//Counting sort
void count_sort(vector<int> &v){
	int max = 0;
	//Find the maximum value in the array 
	for(int i = 0; i < v.size();i++){
		if(max < v[i]){
			max = v[i];
		}
	}
	//Create auxiliary array
	vector<int> result;//Array of last sort results 
	result.resize(v.size());
	vector<int> count; //Counting array
	count.resize(max+1);
	//Start counting 
	for(int i = 0;i < v.size();i++){
		count[v[i]]++;
	} 
	//In order to maintain the stability of counting and sorting, it is necessary to calculate the accumulation array
	//The advantage of an additive array is that it can record the last position of the same element in the original array 
	for(int i = 1;i < count.size();i++){
		count[i] = count[i] + count[i-1];
	} 
	//Traverse the original array in reverse order, and assign to the result array 
	for(int i = v.size()-1;i >=0;i--){
		int index = count[v[i]]-1;//The relative position of the number of the original array, corresponding to the relative position of the result array
		result[index] = v[i];
		count[v[i]]--;//Because there are repeating elements, you need to subtract one. 
	}
	//Copy result array to element group
	for(int i = 0;i < result.size();i++){
		v[i] = result[i];
	} 
} 

1. Cardinality sort (one of bucket sort):

//Radix sorting
void radix_sort(vector<int> &v){
	int max = 0;
	//Find the maximum value in the array 
	for(int i = 0;i < v.size();i++){
		if(max < v[i]){
			max = v[i];
		}
	}
	int k = 0;//The number of digits of the largest number, i.e. k cardinal numbers are required 
	while(max!=0){
		k++;
		int num = max % 10;//Calculate each bit
		max = max/10; 
	}
	vector<int> result;//Result array 
	result.resize(v.size());
	vector<int> count;//Counting array 
	count.resize(10);//Each number is from 0-9, so it needs 10 lengths 
	for(int m = 0;m < k;m++){
		
		//Here's the count sort
		int division = pow(10,m);//Calculate the value divided by each time, i.e. 1, 10100
		//Find the count array 
		for(int i = 0;i < v.size();i++){
			int num = v[i]/division % 10;//Calculate each bit 
			count[num]++; 
		} 
		//Find the accumulation array 
		for(int i = 1;i < count.size();i++){
			count[i] = count[i] + count[i-1];
		}
		//Find the result array
		for(int i = v.size()-1;i >=0;i--){
			int n = v[i]/division % 10;//Calculate the number of current bits for each value 
			int index = count[n]-1;
			result[index] = v[i];
			count[n]--;//Because there are duplicate numbers, you need to subtract one 
		}
		for(int i = 0;i < result.size();i++){
			v[i] = result[i];
		}
		//count array empty 
		for(int i = 0;i < count.size();i++){
			count[i] = 0;
		} 
	}
	
} 

1. Heap sort:

//Adjusting reactor
void heapify(vector<int> &v,int len,int pos){
	if(len <= pos){
		return;
	}
	int left = pos * 2 + 1;//Left node 
	int right = pos * 2 +2;//Right node
	int max = pos;//The default current location is the maximum
	if(left < len && v[max] < v[left]){
		max = left;
	} 
	if(right < len && v[max] < v[right]){
		max = right;
	}
	if(max != pos){
		swap(v[max],v[pos]);
		heapify(v,len,max);
	}
} 
//Build heap
void build_heap(vector<int> &v){
	int lastNode = v.size() - 1;
	int parent = (lastNode - 1) / 2;
	for(int i = parent;i >= 0;i--){
		heapify(v,v.size(),i);
	}
} 
//Heap sort
void heap_sort(vector<int> &v){
	//Build a given array as a heap 
	build_heap(v);
	for(int i = v.size()-1;i >= 0;i--){
		swap(v[i],v[0]);//Last node and root node exchange 
		heapify(v,i,0);
	}
} 

Binary search:

//Binary search, return to find the subscript of the number, not found return - 1 
int binary_search(vector<int> v,int key){//v is the ordered array 
	if(v.size()==0){
		return -1;//not found 
	}
	int low = 0;
	int high = v.size()-1;
	int mid = 0;
	while(low <= high){
		mid = (low+high)/2;
		if(v[mid]==key){
			return mid;
		}else if(v[mid] > key){
			high = mid-1;//Find from front half 
		}else{
			low = mid +1;//Find from the second half 
		}
	}
	return -1;
}