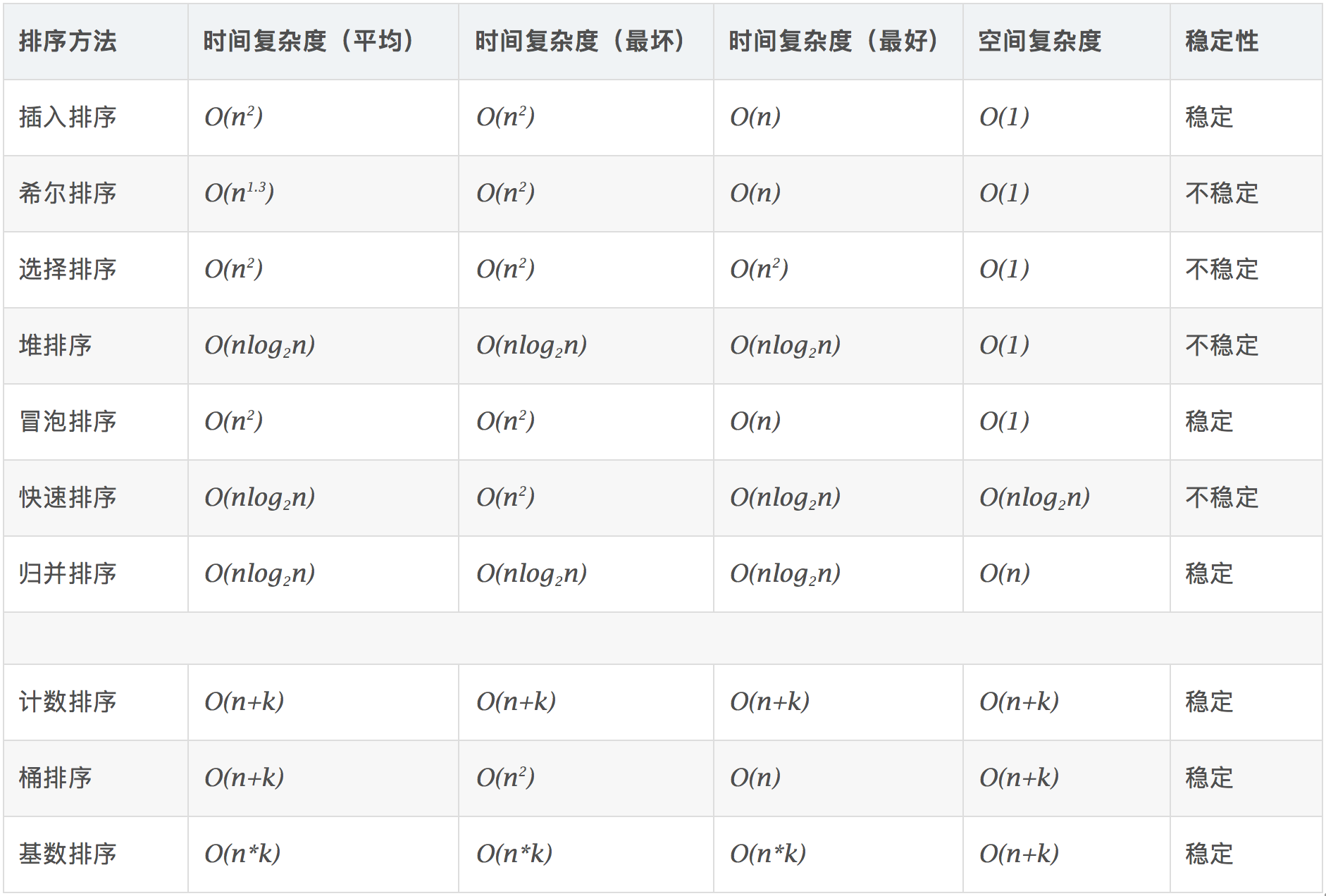
Sorting algorithm
The complexity of each sorting algorithm is as follows:
1. Bubble Sort
- Bubble sorting is a simple sorting algorithm.
- It repeatedly visits the sequence to be sorted, compares two elements at a time, and exchanges them if they are in the wrong order.
- A total of (arr.length - 1) rounds of sorting are performed, and the number of times of each round of sorting is reduced.
- The name of this algorithm comes from the fact that smaller elements will slowly "float" to the top of the sequence through exchange.
Sketch Map
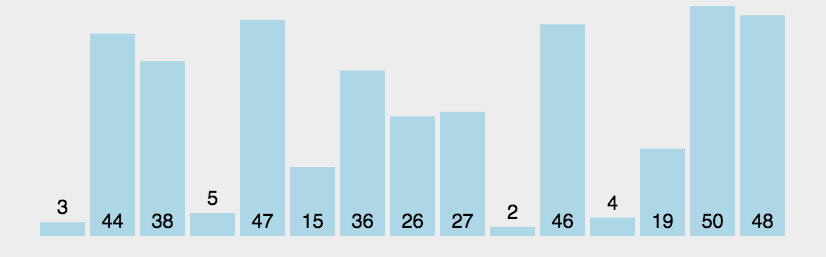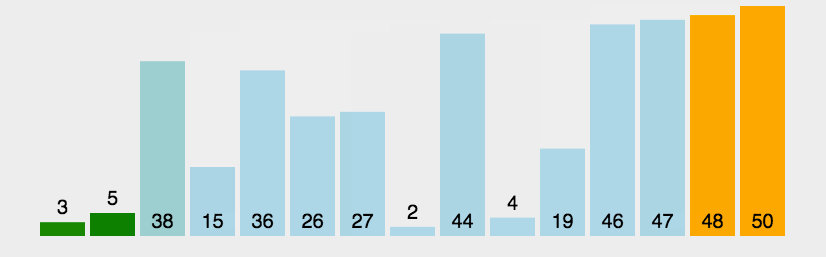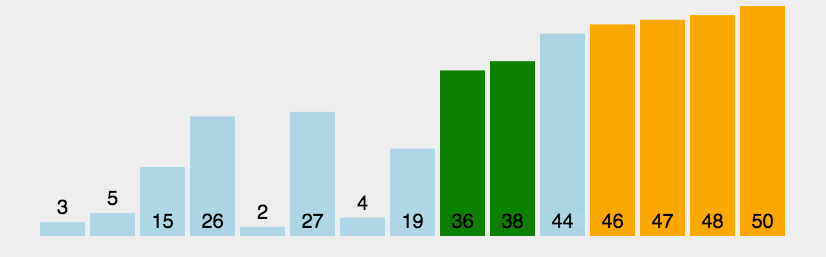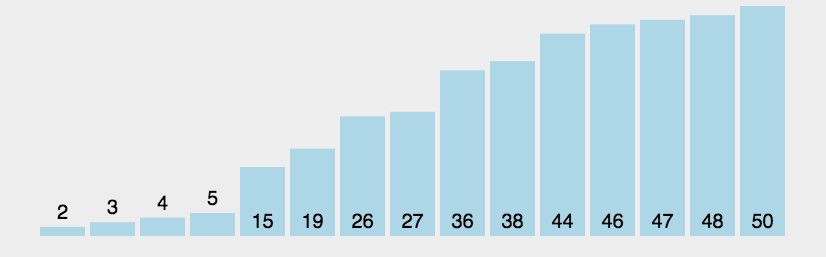
code
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
- If there is no exchange in a round of sorting, you can end the sorting in advance by setting flag.
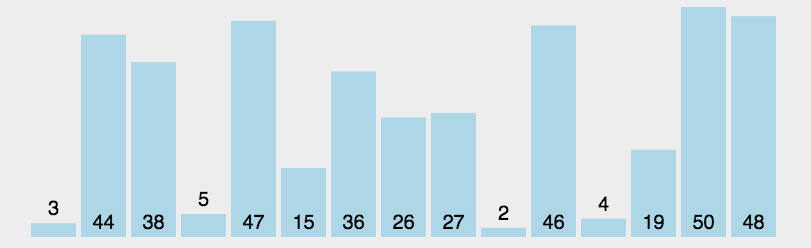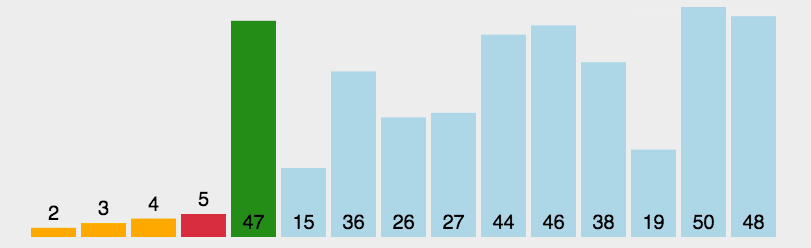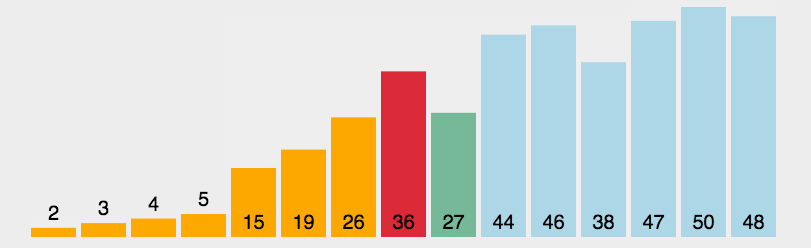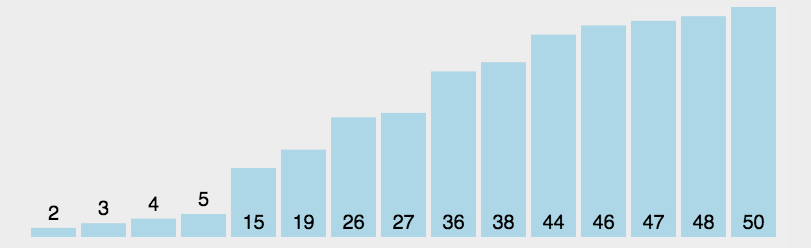
2. Select Sort
- First, find the smallest element in the array,
- Second, swap it with the first element of the array (if the first element is the smallest element, it will swap with itself).
- Second, find the smallest of the remaining elements and swap it with the second element of the array.
- This goes back and forth until the entire array is sorted. This method is called selective sorting.
Sketch Map
code
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = arr[i]; // Assume that the current number is the lowest decimal
int minIndex = i; // Write down the subscript of the lowest decimal
// Compare with each of the following numbers, if there is a smaller number than the current one
// Redefine min and minIndex
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < min) {
min = arr[j];
minIndex = j;
}
}
// If the current number of this round is not the minimum value, that is, the current number and the minimum value exchange positions
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
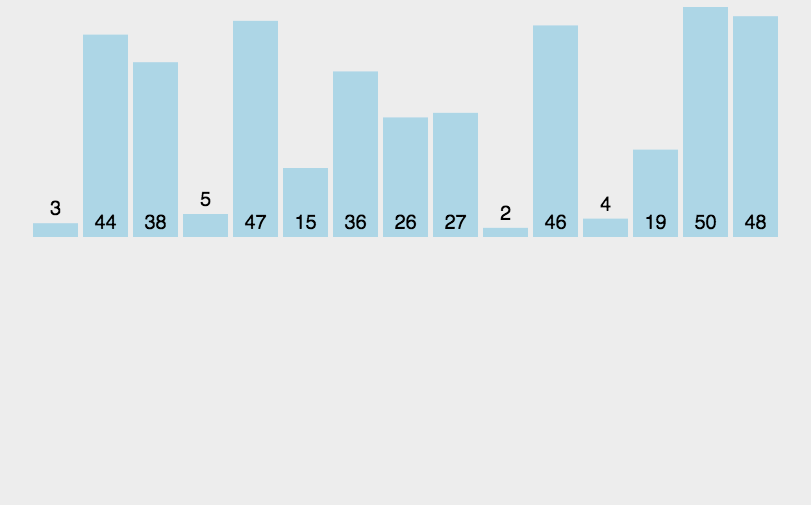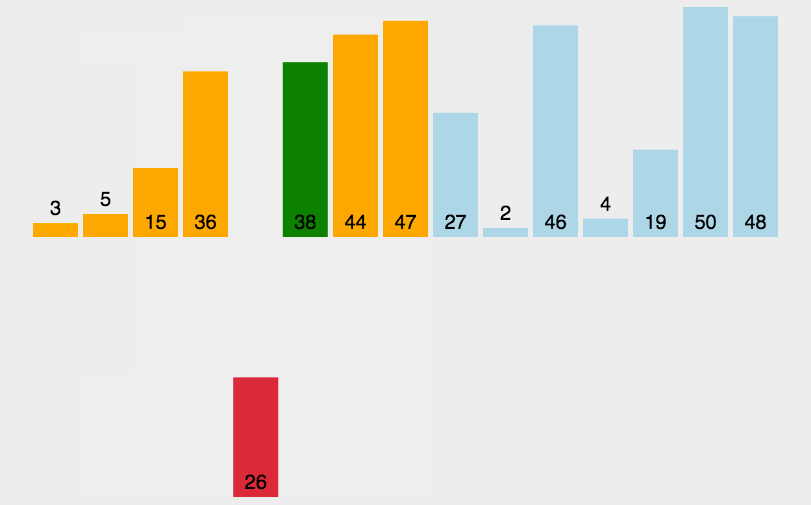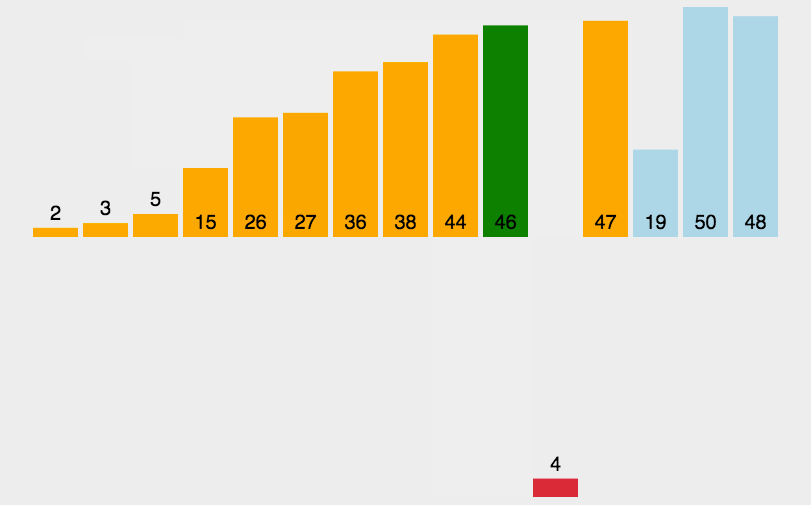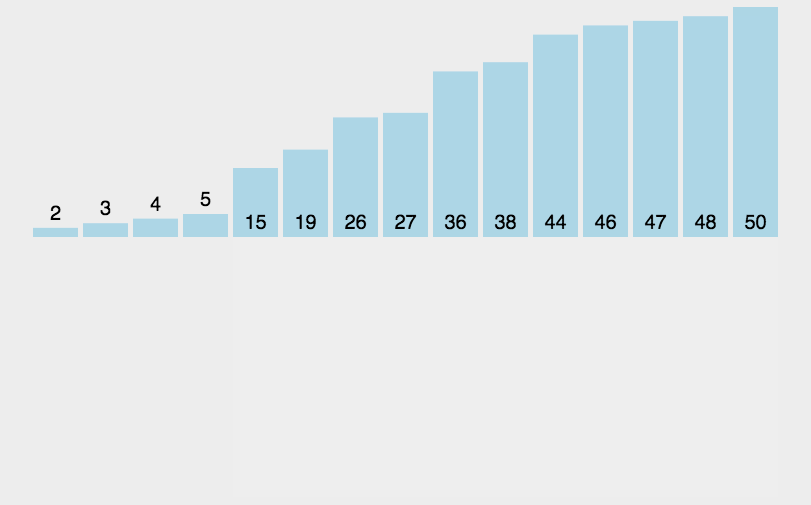
3. Insert Sort
3.1 basic ideas
In each step, a data to be sorted is inserted into the previously ordered sequence until all elements are inserted.
3.2 algorithm implementation
- Starting from the first element, the element can be considered to have been sorted;
- Take out the next element and scan from back to front in the sorted element sequence;
- If the element (sorted) is larger than the new element, move the element to the next position;
- Repeat step 3 until the sorted element is found to be less than or equal to the position of the new element;
- After inserting the new element into this position;
- Repeat steps 2 to 5.
Sketch Map
code
public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int insertVal = arr[i]; // Number of to be inserted
int insertIndex = i - 1; // The position to be inserted (compared) because it is traversed forward from this number
// Traverse forward. If this element is greater than the number to be inserted, move this element backward
// Exit the loop until an element smaller than the number to be inserted is found
while(insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
// At this point, arr [insertindex] < insertval
// Therefore, the number to be inserted should be inserted at (insertIndex + 1)
arr[insertIndex + 1] = insertVal;
}
}
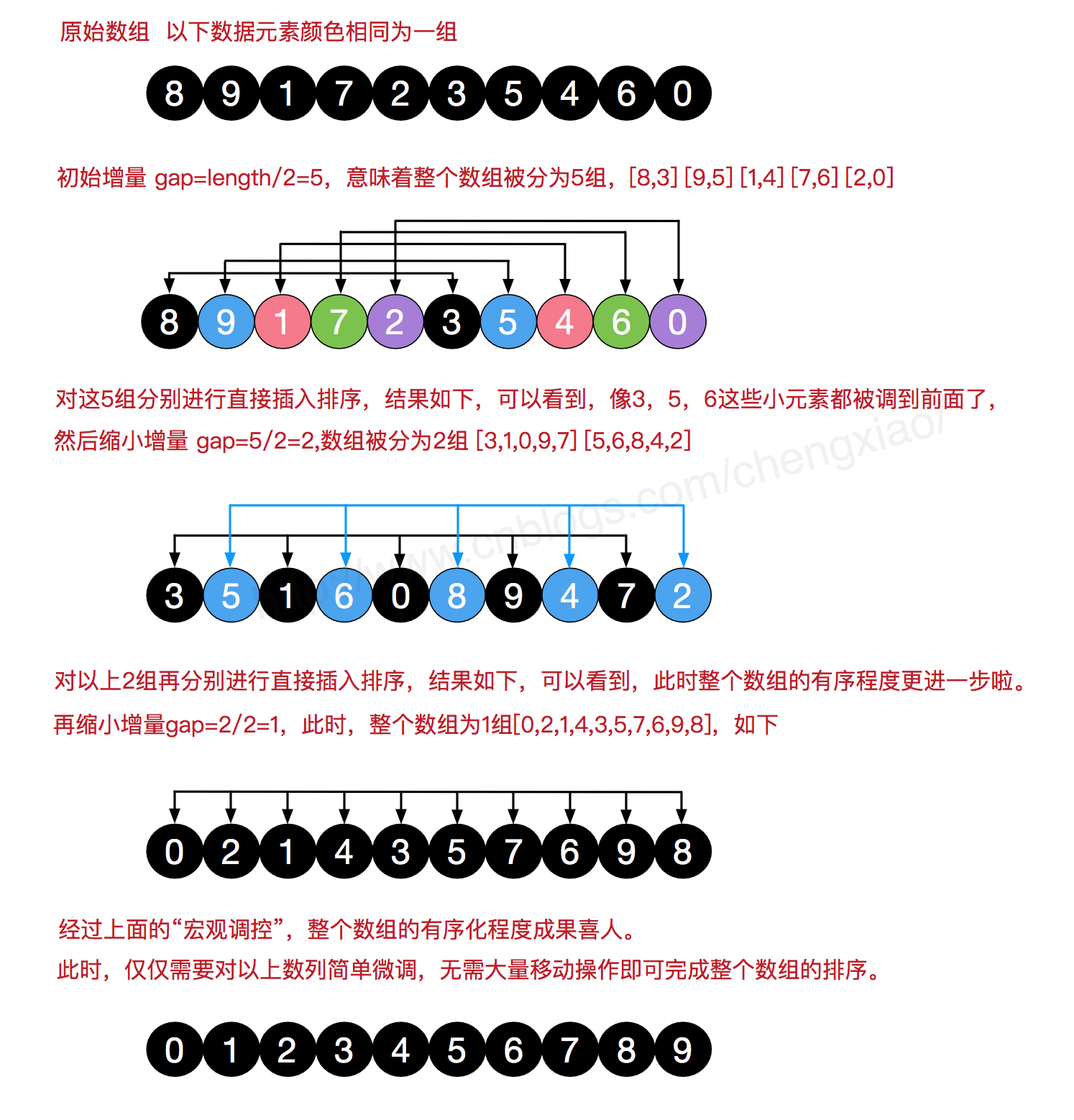
4. Shell Sort
Hill sort is also an insert sort, also known as "narrow incremental sort".
4.1 basic ideas
Hill sort adopts the strategy of jumping grouping in the array. The array elements are divided into several groups through an increment, then grouped for insertion sorting, then gradually reduce the increment, and continue the insertion sorting operation by group until the increment is 1.
4.2 example
code
public static void shellSort(int[] arr) {
int temp = 0;
// Increment gap and gradually reduce the increment
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
// Start with the gap element and sort the groups one by one
for (int i = gap; i < arr.length; i++) {
// Traverse all elements in each group (total gap group), step gap
for (int j = i - gap; j >= 0; j -= gap) {
// If the current element is larger than the element after adding the step, it is exchanged
if (arr[j] > arr[j + gap]) {
temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
}
}
5. Merge Sort
Merge sort is a very typical application of Divide and Conquer.
5.1 basic ideas
The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered.
5.2 algorithm implementation
- The input sequence with length n is divided into two subsequences with length n/2;
- The two subsequences are sorted by merging;
- Merge two sorted subsequences into a final sorting sequence.
Sketch Map
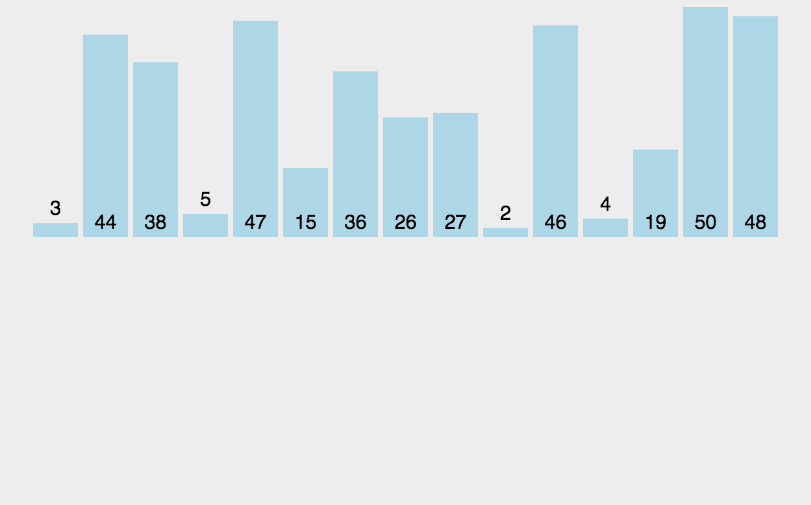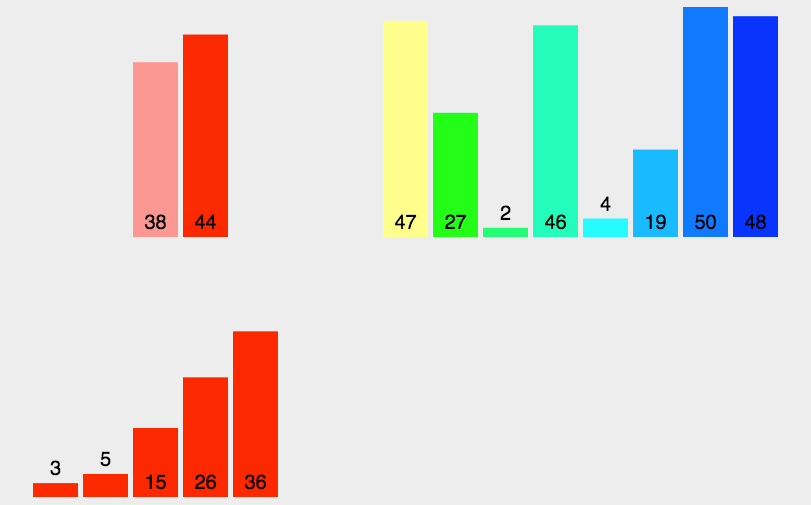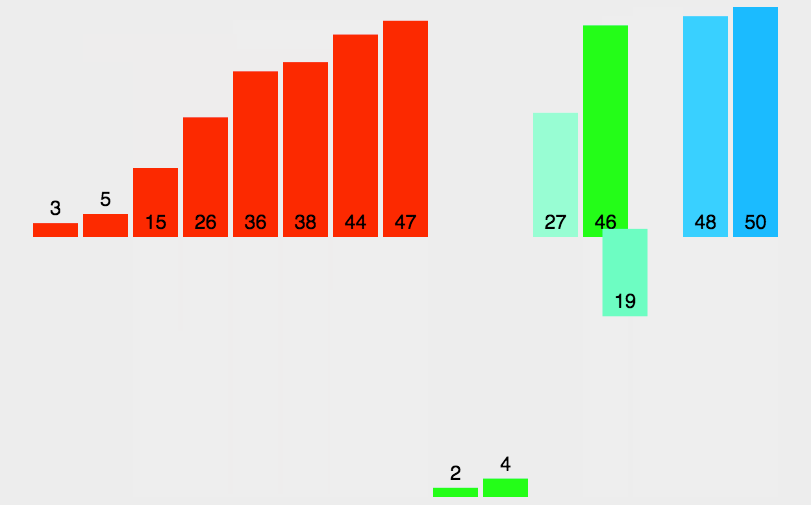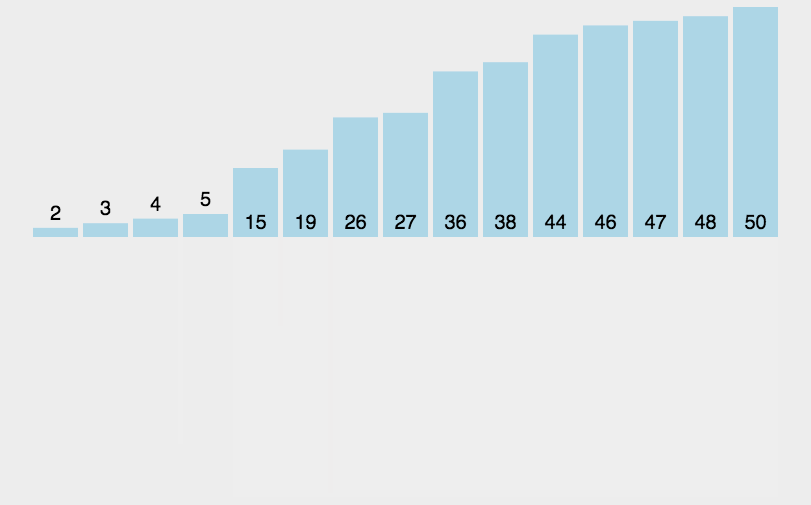
code
// Opening + closing method
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2; // Each time the intermediate index is changed, it is decomposed
// Decompose recursively to the left
mergeSort(arr, left, mid, temp);
// Decompose recursively to the right
mergeSort(arr, mid + 1, right, temp);
// merge
merge(arr, left, mid, right, temp);
}
}
// Merging method
/**
*
* @param arr Sorted original array
* @param left Start index of left ordered sequence
* @param mid Intermediate index
* @param right Right index
* @param temp Index as transit
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // Start index of left ordered sequence
int j = mid + 1; // Start index of the right ordered sequence
int t = 0; // Points to the current index of the temp array
// (1) Fill the left and right data into the temp array according to the rules
// Until one side is finished
while (i <= mid && j <= right) {
// If the current element on the left is smaller than the current element on the right, put the current element on the left into temp
// Then t + +, i++
if (arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
}else { //Conversely, put the current element on the right into temp
temp[t] = arr[j];
t += 1;
j += 1;
}
}
// (2) Fill all the data on the unfinished side into temp in turn
while (i <= mid) { //The left side is incomplete, and there are still elements left
temp[t] = arr[i];
t += 1;
i += 1;
}
while (j <= right) { //The left side is incomplete, and there are still elements left
temp[t] = arr[j];
t += 1;
j += 1;
}
// (3) Copy the elements of temp array to arr
t = 0;
int tempLeft = left;
while (tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}
6. Quick Sort
6.1 basic ideas
- First, take a number from the sequence as the reference number.
- In the partition process, all numbers larger than this number are placed on its right, and all numbers less than or equal to it are placed on its left.
- Repeat the second step for the left and right intervals until there is only one number in each interval.
6.2 algorithm implementation
Take the following arrangement as an example: 3 1 2 5 4 6 9 7 10 8
Start "detection" from both ends of the initial sequence "6 1 2 7 9 3 4 5 10 8". First find a number less than 6 from right to left, then find a number greater than 6 from left to right, and then exchange them.
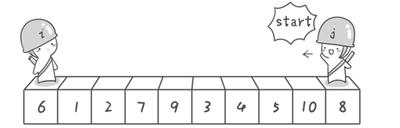
- First the sentry j began to move out.
- Sentry j moves left step by step (i.e. j --) until he finds a number less than 6 and stops.
- Next, sentry I moves to the right step by step (i.e. I + +) until he finds a number greater than 6 and stops.
- Finally, sentry j stopped in front of the number 5 and sentry i stopped in front of the number 7.
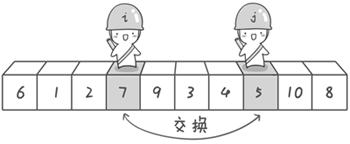
- Exchange the values of the elements pointed to by sentinel i and sentinel j
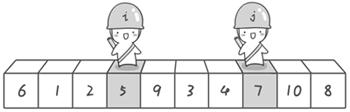
- Here, the first exchange is over
- The sentry j continued to move to the left. He found 4 (smaller than the benchmark 6, meeting the requirements) and stopped
- Sentry i also continued to move to the right. He found 9 (larger than the benchmark number of 6, meeting the requirements) and stopped
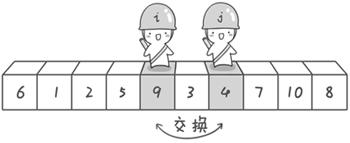
- Exchange again at this time
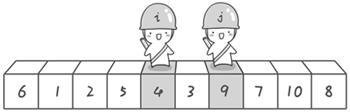
- After the second exchange, the "detection" continues
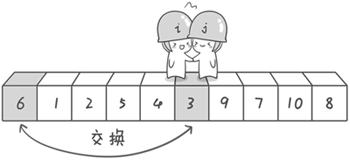
- Sentry j continued to move to the left. He found 3 (smaller than the benchmark 6, meeting the requirements) and stopped again
- The sentry i keeps moving to the right. No! At this time, sentry i and sentry j meet, and sentry i and sentry j both come to 3
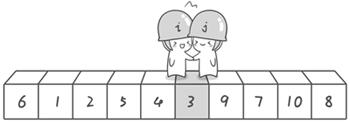
- Indicates that the probe ends. We exchange the reference numbers 6 and 3
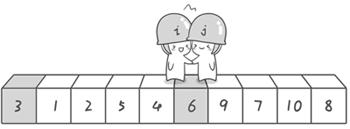
- This is the real end of the first round of "detection".
- At this time, taking the reference number 6 as the dividing point, the numbers on the left of 6 are less than or equal to 6, and the numbers on the right of 6 are greater than or equal to 6.
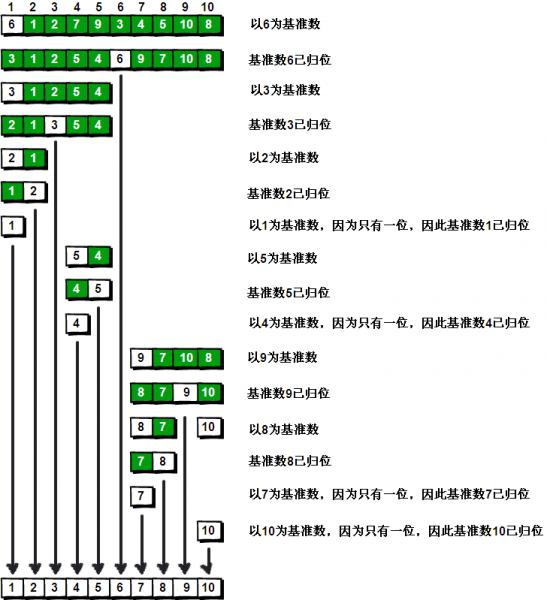
code
public static void quickSort(int[] arr, int left, int right) {
int i = left;
int j = right;
int temp, t;
if (left > right) {
return;
}
temp = arr[left]; // Datum point
while (i < j) {
// The sentry j set out first until he found a number smaller than the reference point
while (temp <= arr[j] && i < j) {
j--;
}
// The sentry i set out until he found a number greater than the reference point
while (temp >= arr[i] && i < j) {
i++;
}
// Exchange when conditions are met
if (i < j) {
t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
// Sentinels i and j meet and exchange the elements of this position with the reference position elements
arr[left] = arr[i]; // At this time, the element of the position is placed in the reference position
arr[i] = temp; // The datum element is placed at this position
// Recursion: sort the queues on the left and right at i=j respectively
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
7. Radix Sort
Cardinality sorting is an extension of bucket sorting.
7.1 basic ideas
Cut the integer into different numbers according to the number of digits, and then compare them respectively according to each number of digits.
7.2 algorithm implementation
- Initialize 10 buckets with subscripts 0 ~ 9;
- Take out the bits of each element to see which bucket it should be placed in;
- Take out the data in the order of buckets and put it into the original array;
- Repeat steps 1 and 2 for the tens, hundreds, thousands... Of each element.
Sketch Map

code
public static void radixSort(int arr[]) {
// Get the number of digits of the largest number in the array
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
int maxLength = (max + "").length(); // Convert to a string and find the length, that is, the number of digits of the maximum number
// Define a two-dimensional array, representing 10 buckets, and each bucket is a one-dimensional array
int[][] bucket = new int[10][arr.length];
// Define a one-dimensional array to record the number of data put into each bucket
int[] bucketElementCounts = new int[10];
for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
// Sort the corresponding bits of each element: single bit -- > ten bit -- > hundred bit -- >
for (int j = 0; j < arr.length; j++) {
// Take out the value of the corresponding bit of each element
int digitOfElement = arr[j] / n % 10;
// Put it in the corresponding bucket
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
// Take out the data in the order of the bucket (array subscript) and put it into the original array
int index = 0;
for (int k = 0; k < bucketElementCounts.length; k++) { // Traverse each bucket
if (bucketElementCounts[k] != 0) {
for (int l = 0; l < bucketElementCounts[k]; l++) { // Traverse each data in the bucket
arr[index++] = bucket[k][l];
}
}
bucketElementCounts[k] = 0;
}
System.out.println("The first" + (i + 1) + "Round, the sorting result is:" + Arrays.toString(arr));
}
}