1. The Idea of Dividing and Governing
The divide-and-conquer idea is mainly realized by recursion, and each level of recursion includes three steps:
- Decomposition: The original problem is divided into several sub-problems. The form of sub-problems should be consistent with the original problem, but the scale is smaller.
- Solution: When the scale of the sub-problem is small enough, stop recursion, solve the sub-problem, get the solution result of the sub-problem and return to the upper level.
- Merge: Merge the results of sub-problems to get the solution of the original problem.
In other words, the idea of dividing and conquering is to decompose a big problem into innumerable sub-problems with recursive layers. These sub-problems should be guaranteed to be of the same type as the original problem, except that they are smaller and easier to solve, but the solving process is the same.
2. Merging and Sorting Algorithms
1. Consider: If we were given two sorted arrays (the same sorting rule) A and B, how would we merge them into an ordered array C?
The problem is very simple. Compare elements from two arrays and put them in C. If both A and B arrays have only one element, they all become an ordered array, then they can be directly compared and placed in the array C, returning the ordered array C.
2. Divide the sorting problem of disordered arrays by dividing and conquering: an array of disordered arrays
(1) Decomposition: Unordered arrays are divided recursively into two arrays from array.length/2 at a time until the size of the subarrays is 1.
(2) Solution: When the size of the subarray is 1, the smallest size of the array has automatically changed into an ordered array, and the result of the ordered array is returned by recursive termination.
(3) Merge: Receive two ordered subarrays returned by the next level recursion, merge the data of these two ordered subarrays into a new ordered array, and then return the ordered array to the upper level recursion.
3. Sorting examples: In order to understand recursive partitioning arrays, we can build a recursive tree graph (it is more convenient to understand recursion). Taking the array int[] arr = {3,23,4,13,4,5,63,6,2} as an example, its array partition tree graph is as follows
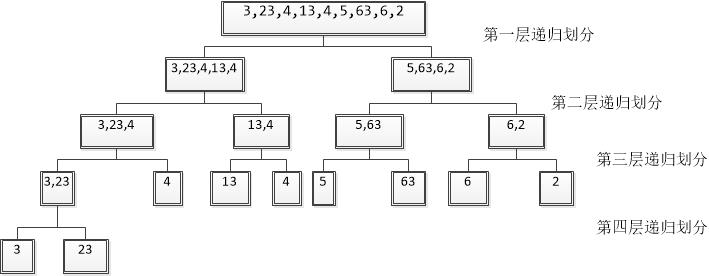
The next step is to return the sorted array of leaf nodes to the upper level of recursion, process and merge a new ordered array in the upper level, and then return to the upper level. Repeat this step until the root node level can turn the original array into an ordered array.
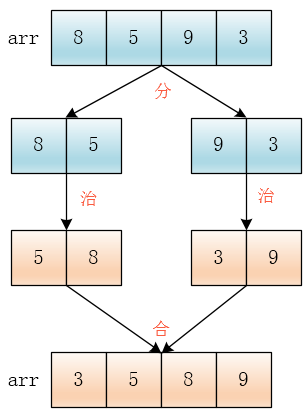
That is to say, the method of recursive invocation in merging algorithm is mainly composed of two parts, namely, dividing arrays and combining arrays (merging two ordered arrays). The pseudocode is as follows
merge(int[] arr){ if(arr.length < 2){ return arr;//If the length of the incoming array is 1, return directly } int[] left = splitLeft(arr);//Partition to get left subarray int[] right = spliteRight(arr);//Partition to get right subarray left = merge(left);//Recursive calls to get sorted left subarrays right = merge(right);//Recursive calls to get sorted right subarrays arr = sort(left,right);//Combining left and right ordered subnumbers into an ordered array return arr;//Return }
Specific code implementation (an example written by a person based on algorithmic logic, dividing left and right sub-arrays are all newly created arrays for assignment, which has high spatial complexity and time complexity, but is mainly easy to understand)
Personal realization:
/** * * @Description:Divide and conquer algorithm, using recursion, divides an array element into two arrays continuously until the array is divided into only one element. * Then it returns to the upper layer, mainly to ensure that the two arrays returned to the upper layer are arranged arrays, sorted and merged in the upper layer, and then returned. * You can finally get an ordered array. */ public class Sort { public static int[] merge(int[] arr){ int left = 0; int right = arr.length; if (right == 1) { int[] endArr = {arr[left]}; return endArr; } //Array partition int mid = (left + right) / 2; int[] leftArr = new int[mid-left]; int[] rightArr = new int[right - mid]; for (int i = 0; i <= mid-1; i++) { leftArr[i] = arr[i]; } for (int i = 0,j=mid; i < rightArr.length && j < arr.length; i++,j++) { rightArr[i] = arr[j]; } //Recursive calls to get left and right subarrays of sorted completion leftArr = merge(leftArr); rightArr = merge(rightArr); //Merge two arrays and sort them return sort(arr, leftArr, rightArr); } public static int[] sort(int[] arr, int[] left, int[] right){ int i = 0; int j = 0; for (int index = 0; index < arr.length; index++){ if (i >= left.length && j < right.length) { arr[index] = right[j]; j++; continue; } if (j >= right.length && i < left.length) { arr[index] = left[i]; i++; continue; } if (left[i] > right[j]){ arr[index] = right[j]; j++; } else { arr[index] = left[i]; i++; } } return arr; } public static void main(String[] args) { int[] arr = {3,23,4,13,4,5,63,6,2}; for(int i:merge(arr)) { System.out.println(i); } } }
Better implementation:
public class Solution { /* * @param A:an integer array * @return: */ public voidsortIntegers2(int[] A) { // writeyour code here //Sorting Array A by Merge Sorting mergeSort(A,0,A.length-1); } //Merge Sort public void mergeSort(int[] A,int start,int end){ if(start>=end) return; int middle= (start+end)/2; mergeSort(A,start,middle); mergeSort(A,middle+1,end); //Temporary arrays to be allocated for merge sort //This is the core of merge sort. int []temp = new int[end-start+1]; inti=start; int j =middle+1; intindex=0; while(i<=middle&&j<=end){ if(A[i]<=A[j]){ temp[index++] = A[i++]; }else{ temp[index++] = A[j++]; } } while(i<=middle){ temp[index++] =A[i++]; } while(j<=end){ temp[index++] =A[j++]; } i=start; index = 0; for(;i<=end;i++){ A[i] =temp[index++]; } } }