Sorting API

1. Static sorting API in arrays class

• **Arrays. Sort (data type [] a) uses quick sort, and the time complexity is O(nlogn)

Sorts the specified array of types in ascending numerical order. instable

• Arrays.sort(T[],Comparator<? super T> c) ,Arrays.sort(Object[] a)

The specified object array is sorted according to the order generated by the specified comparator. When c=null, it is sorted in natural order

The sorting algorithm is a modified merge sorting algorithm (where the merge is ignored if the highest element in the low sublist is less than the lowest element in the high sublist). This algorithm provides guaranteed n*log(n) performance. stable

2. Collections static sorting API

Collections. Sort (list), and collections sort(List list，Comparator<？super T> c);

The sorting used is stable, mainly for list sorting

The sorting algorithm is a modified merge sorting algorithm (where the merge is ignored if the highest element in the low sublist is less than the lowest element in the high sublist). This algorithm provides guaranteed n log(n) performance.
This implementation dumps the specified list into an array, sorts the array, and iterates over the list of each element at the corresponding position in the reset array. This avoids the problem of trying to sort the linked list in place
n2 log(n) performance.

3. Sorting API of ArrayList

list. sort(Comparator<? super T> c); Sort the list in natural order when c=null

1. To sort the list, you can use the sort method of the list itself or the static sorting method of Collections, and the sorting methods of Collections are stable

2. Static sort of Arrays, one is fast sort and the other is merge sort (stable)

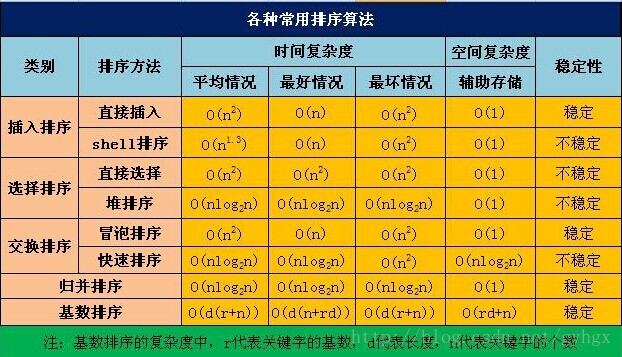
Supplement: common sorting methods

classification

1. Insert sort: direct insert sort, dichotomy insert sort, Hill sort.
2. Select sort: simple select sort and heap sort.
3. Swap sort: bubble sort and quick sort.
4. Merge sort
5. Cardinality sort

Quick sort

Quicksort is an improvement on bubble sort. Proposed by C. A. R. Hoare in 1962

Algorithmic thought

Sort the to be sorted by one pass Data segmentation It is divided into two independent parts. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can recursion So that the whole data becomes an ordered sequence.

① Taking the first keyword K 1 as the control word, divide [K 1, K 2,..., K n] into two sub areas, so that all keywords in the left area are less than or equal to K 1, and all keywords in the right area are greater than or equal to K 1. Finally, the control word occupies an appropriate position in the middle of the two sub areas. In the sub area, the data is still in disorder.
② Take the left area as a whole and process it with the steps of ①, and the right area performs the same process. (i.e. recursion)
③ Repeat steps ① and ② until the left area is processed.

static void quicksort(int n[],int left,int right) {
        int dp;
        if (left < right) {
            dp = partition(n, left, right);
            quicksort(n, left, dp -1);
            quicksort(n, dp +1, right);
        }
    }
 
    static int partition(int n[],int left,int right) {
        int pivot = n[left];
        while (left < right) {
            while (left < right && n[right] >= pivot)
                right--;
            if (left < right)
                n[left++] = n[right];
            while (left < right && n[left] <= pivot)
                left++;
            if (left < right)
                n[right--] = n[left];
        }
        n[left] = pivot;
        return left;
    }

Merge sort

Merge sorting method is to merge two (or more) ordered tables into a new ordered table, that is, the sequence to be sorted is divided into several subsequences, and each subsequence is ordered. Then the ordered subsequences are combined into an overall ordered sequence.

public static int[] sort(int[] a,int low,int high){
        int mid = (low+high)/2;
        if(low<high){
            sort(a,low,mid);
            sort(a,mid+1,high);
            //Left and right merging
            merge(a,low,mid,high);
        }
        return a;
    }
     
    public static void merge(int[] a,int low,int mid,int high) {
        int[] temp =new int[high-low+1];
        int i= low;
        int j = mid+1;
        int k=0;
        // Move the smaller number to the new array first
        while(i<=mid && j<=high){
            if(a[i]<a[j]){
                temp[k++] = a[i++];
            }else{
                temp[k++] = a[j++];
            }
        }
        // Move the remaining number on the left into the array 
        while(i<=mid){
            temp[k++] = a[i++];
        }
        // Move the remaining number on the right side into the array
        while(j<=high){
            temp[k++] = a[j++];
        }
        // Overwrite the num array with the number in the new array
        for(int x=0;x<temp.length;x++){
            a[x+low] = temp[x];
        }
    }