Java7 HashMap
HashMap is the simplest. First, we are very familiar with it. Second, it does not support concurrent operations, so the source code is also very simple.
First, let's use the following figure to introduce the structure of HashMap.

This is only a schematic diagram, because it does not take into account the expansion of the array, which will be discussed later.
In the general direction, there is an array in the HashMap, and then each element in the array is a one-way linked list.
In the figure above, each green entity is an instance of the nested class Entry. The Entry contains four attributes: key, value, hash value and next for one-way linked list.
Capacity: the current array capacity, which is always 2^n, can be expanded. After expansion, the array size is twice the current size.
loadFactor: load factor, which is 0.75 by default.
Threshold: the threshold of capacity expansion, equal to capacity * loadFactor
put process analysis
It's still relatively simple. Follow the code again.
public V put(K key, V value) {
// When inserting the first element, you need to initialize the array size first
if (table == EMPTY_TABLE) {
inflateTable(threshold);
}
// If the key is null, those interested can look inside and finally put the entry into table[0]
if (key == null)
return putForNullKey(value);
// 1. Find the hash value of the key
int hash = hash(key);
// 2. Find the corresponding array subscript
int i = indexFor(hash, table.length);
// 3. Traverse the linked list at the corresponding subscript to see if there are duplicate key s,
// If so, it is over when the put method returns the old value
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
// 4. There are no duplicate key s. Add this entry to the linked list. The details will be described later
addEntry(hash, key, value, i);
return null;
}
Array initialization
When the first element is inserted into the HashMap, do an array initialization, that is, first determine the initial array size and calculate the threshold of array expansion.
private void inflateTable(int toSize) {
// Ensure that the size of the array must be to the nth power of 2.
// For example, if you initialize new HashMap(20), the initial array size is 32
int capacity = roundUpToPowerOf2(toSize);
// Calculate capacity expansion threshold: capacity * loadFactor
threshold = (int) Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);
// It's an initialization array
table = new Entry[capacity];
initHashSeedAsNeeded(capacity); //ignore
}
Here is an approach to keep the array size to the nth power of 2. The HashMap and ConcurrentHashMap of Java 7 and Java 8 have corresponding requirements, but the implementation code is slightly different, which will be seen later.
Calculate specific array position
This is simple. We can YY one ourselves: use the hash value of the key to modulo the array length.
static int indexFor(int hash, int length) {
// assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";
return hash & (length-1);
}
This method is very simple, that is to take the lower n bits of the hash value. For example, when the array length is 32, it actually takes the lower 5 bits of the hash value of the key as its subscript position in the array.
Add node to linked list
After the array subscript is found, the key duplication will be judged first. If there is no repetition, the new value will be put into the header of the linked list.
void addEntry(int hash, K key, V value, int bucketIndex) {
// If the current HashMap size has reached the threshold and there are already elements in the array position where the new value is to be inserted, the capacity should be expanded
if ((size >= threshold) && (null != table[bucketIndex])) {
// Capacity expansion will be introduced later
resize(2 * table.length);
// After capacity expansion, recalculate the hash value
hash = (null != key) ? hash(key) : 0;
// Recalculate the new subscript after capacity expansion
bucketIndex = indexFor(hash, table.length);
}
// Look down
createEntry(hash, key, value, bucketIndex);
}
// This is very simple. In fact, it is to put the new value into the header of the linked list, and then size++
void createEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex];
table[bucketIndex] = new Entry<>(hash, key, value, e);
size++;
}
The main logic of this method is to first judge whether capacity expansion is needed. If necessary, expand the capacity first, and then insert the new data into the header of the linked list at the corresponding position of the expanded array.
Array expansion
As we saw earlier, when inserting a new value, if the current size has reached the threshold and there are elements in the array position to be inserted, the capacity expansion will be triggered. After the capacity expansion, the array size will be twice the original size.
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
// New array
Entry[] newTable = new Entry[newCapacity];
// Migrate the values from the original array to a new larger array
transfer(newTable, initHashSeedAsNeeded(newCapacity));
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}
Capacity expansion is to replace the original small array with a new large array, and migrate the values in the original array to the new array.
Due to the double expansion, all nodes of the linked list in the original table[i] will be split into newTable[i] and newTable[i + oldLength] positions of the new array during the migration process. If the length of the original array is 16, all elements in the linked list at the original table[0] will be allocated to newTable[0] and newTable[16] in the new array after capacity expansion. The code is relatively simple, so I won't expand it here.
get process analysis
Compared with the put process, the get process is very simple.
- Calculate the hash value according to the key.
- Find the corresponding array subscript: hash & (length - 1).
- Traverse the linked list at the position of the array until an equal (= = or equals) key is found.
public V get(Object key) {
// As mentioned earlier, if the key is null, it will be placed in table[0], so just traverse the linked list at table[0]
if (key == null)
return getForNullKey();
//
Entry<K,V> entry = getEntry(key);
return null == entry ? null : entry.getValue();
}
getEntry(key):
final Entry<K,V> getEntry(Object key) {
if (size == 0) {
return null;
}
int hash = (key == null) ? 0 : hash(key);
// Determine the array subscript, and then traverse the linked list from scratch until it is found
for (Entry<K,V> e = table[indexFor(hash, table.length)];
e != null;
e = e.next) {
Object k;
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
}
return null;
}
Java7 ConcurrentHashMap
Concurrent HashMap has the same idea as HashMap, but it is more complex because it supports concurrent operations.
The entire ConcurrentHashMap is composed of segments, which represent the meaning of "part" or "paragraph", so it will be described as segment lock in many places. Note that in the text, I use "slot" to represent a segment in many places.
The simple understanding is that ConcurrentHashMap is an array of segments. Segments are locked by inheriting ReentrantLock, so each operation that needs to be locked locks a segment. In this way, as long as each segment is thread safe, global thread safety is realized.
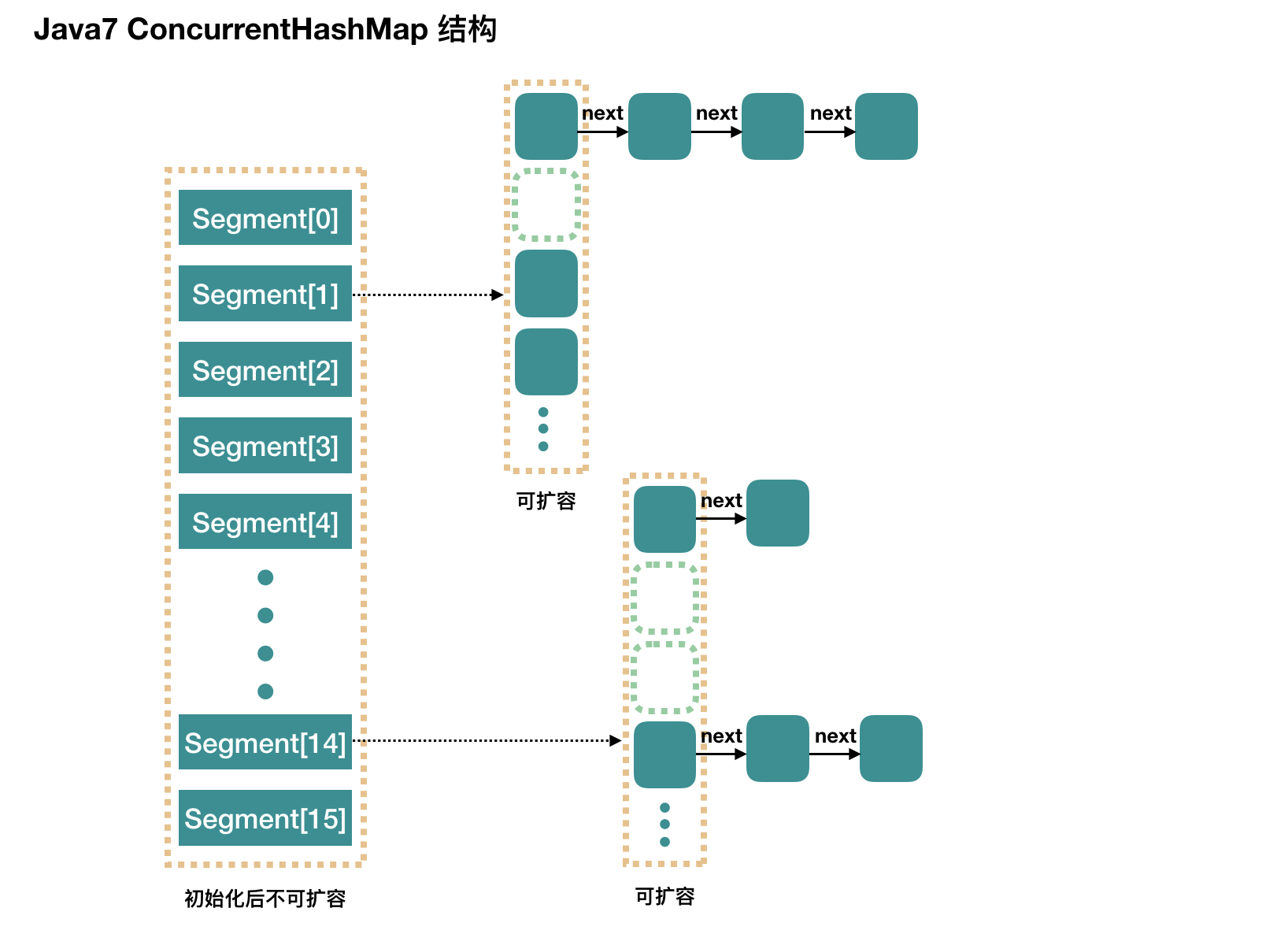
concurrencyLevel: parallel level, number of concurrent threads and number of Segments. It doesn't matter how to translate them. The default value is 16, that is, there are 16 Segments in ConcurrentHashMap. Therefore, theoretically, at most 16 threads can write concurrently at this time, as long as their operations are distributed on different Segments. This value can be set during initialization Is other values, but once initialized, it cannot be expanded.
Specifically, each Segment is very similar to the HashMap described earlier, but it needs to ensure thread safety, so it needs to be handled more troublesome.
initialization
initialCapacity: initial capacity. This value refers to the initial capacity of the entire ConcurrentHashMap. It needs to be evenly distributed to each Segment during actual operation.
loadFactor: load factor. As we said before, the Segment array cannot be expanded, so this load factor is used internally for each Segment.
public ConcurrentHashMap(int initialCapacity,
float loadFactor, int concurrencyLevel) {
if (!(loadFactor > 0) || initialCapacity < 0 || concurrencyLevel <= 0)
throw new IllegalArgumentException();
if (concurrencyLevel > MAX_SEGMENTS)
concurrencyLevel = MAX_SEGMENTS;
// Find power-of-two sizes best matching arguments
int sshift = 0;
int ssize = 1;
// Calculate the parallelism level ssize because you want to keep the parallelism level to the nth power of 2
while (ssize < concurrencyLevel) {
++sshift;
ssize <<= 1;
}
// Let's not burn our brains here. Use the default value. concurrencyLevel is 16 and sshift is 4
// Then calculate that the segmentShift is 28 and the segmentMask is 15. These two values will be used later
this.segmentShift = 32 - sshift;
this.segmentMask = ssize - 1;
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// initialCapacity sets the initial size of the entire map,
// Here, the size of each position in the Segment array can be calculated according to initialCapacity
// If the initialCapacity is 64, each Segment or "slot" can be divided into 4
int c = initialCapacity / ssize;
if (c * ssize < initialCapacity)
++c;
// Default min_ SEGMENT_ TABLE_ Capability is 2. This value is also important, because in this case, for a specific slot,
// Inserting one element does not result in capacity expansion, but only when inserting the second element
int cap = MIN_SEGMENT_TABLE_CAPACITY;
while (cap < c)
cap <<= 1;
// Create a Segment array,
// And create the first element of the array, segment[0]
Segment<K,V> s0 =
new Segment<K,V>(loadFactor, (int)(cap * loadFactor),
(HashEntry<K,V>[])new HashEntry[cap]);
Segment<K,V>[] ss = (Segment<K,V>[])new Segment[ssize];
// Write segment[0] to array
UNSAFE.putOrderedObject(ss, SBASE, s0); // ordered write of segments[0]
this.segments = ss;
}
After initialization, we get a Segment array.
We will use the new ConcurrentHashMap() parameterless constructor for initialization. After initialization:
- The length of Segment array is 16 and cannot be expanded
- The default size of Segment[i] is 2, the load factor is 0.75, and the initial threshold is 1.5, that is, inserting the first element will not trigger capacity expansion, and inserting the second element will carry out the first capacity expansion
- segment[0] is initialized here, and other locations are still null. As for why segment[0] should be initialized, the following code will introduce it
- At present, the value of segmentShift is 32 - 4 = 28 and the value of segmentMask is 16 - 1 = 15. Let's simply translate them into shift and mask, which will be used soon
put process analysis
Let's first look at the main process of put. Some key details will be introduced in detail later.
public V put(K key, V value) {
Segment<K,V> s;
if (value == null)
throw new NullPointerException();
// 1. Calculate the hash value of the key
int hash = hash(key);
// 2. Find the position j in the Segment array according to the hash value
// hash is 32 bits, shift the segmentShift(28) bits to the right without sign, leaving the upper 4 bits,
// Then perform an and operation with segmentMask(15), that is, j is the upper 4 bits of the hash value, that is, the array subscript of the slot
int j = (hash >>> segmentShift) & segmentMask;
// As I just said, segment[0] is initialized during initialization, but other locations are still null,
// Ensuesegment (J) initializes segment[j]
if ((s = (Segment<K,V>)UNSAFE.getObject // nonvolatile; recheck
(segments, (j << SSHIFT) + SBASE)) == null) // in ensureSegment
s = ensureSegment(j);
// 3. Insert the new value into slot s
return s.put(key, hash, value, false);
}
The first layer is very simple. You can quickly find the corresponding Segment according to the hash value, and then the put operation inside the Segment.
The interior of Segment is composed of array + linked list.
final V put(K key, int hash, V value, boolean onlyIfAbsent) {
// Before writing to the segment, you need to obtain the exclusive lock of the segment
// Let's look at the main process first, and we will introduce this part in detail later
HashEntry<K,V> node = tryLock() ? null :
scanAndLockForPut(key, hash, value);
V oldValue;
try {
// This is an array inside segment
HashEntry<K,V>[] tab = table;
// Then use the hash value to find the array subscript that should be placed
int index = (tab.length - 1) & hash;
// first is the header of the linked list at this position of the array
HashEntry<K,V> first = entryAt(tab, index);
// Although the following string of for loops is very long, it is also easy to understand. Think about the two cases where there are no elements at this position and there is already a linked list
for (HashEntry<K,V> e = first;;) {
if (e != null) {
K k;
if ((k = e.key) == key ||
(e.hash == hash && key.equals(k))) {
oldValue = e.value;
if (!onlyIfAbsent) {
// Overwrite old value
e.value = value;
++modCount;
}
break;
}
// Continue to follow the linked list
e = e.next;
}
else {
// Whether the node is null or not depends on the process of obtaining the lock, but it has nothing to do with here.
// If it is not null, set it directly as the linked list header; If it is null, initialize and set it as the linked list header.
if (node != null)
node.setNext(first);
else
node = new HashEntry<K,V>(hash, key, value, first);
int c = count + 1;
// If the threshold of the segment is exceeded, the segment needs to be expanded
if (c > threshold && tab.length < MAXIMUM_CAPACITY)
rehash(node); // The expansion will also be analyzed in detail later
else
// If the threshold is not reached, put the node in the index position of the array tab,
// In fact, the new node is set as the header of the original linked list
setEntryAt(tab, index, node);
++modCount;
count = c;
oldValue = null;
break;
}
}
} finally {
// Unlock
unlock();
}
return oldValue;
}
The overall process is relatively simple. Due to the protection of exclusive lock, the internal operation of segment is not complex. As for the concurrency problem, we will introduce it later.
Here, the put operation is over. Next, let's talk about some key operations.
Initialization slot: ensuesegment
During the initialization of ConcurrentHashMap, the first slot segment[0] will be initialized. For other slots, it will be initialized when the first value is inserted.
Concurrency needs to be considered here, because it is likely that multiple threads will come in to initialize the same slot segment[k] at the same time, but as long as one succeeds.
private Segment<K,V> ensureSegment(int k) {
final Segment<K,V>[] ss = this.segments;
long u = (k << SSHIFT) + SBASE; // raw offset
Segment<K,V> seg;
if ((seg = (Segment<K,V>)UNSAFE.getObjectVolatile(ss, u)) == null) {
// Here we see why segment[0] should be initialized before,
// Initialize segment[k] with the array length and load factor at the current segment[0]
// Why use "current" because segment[0] may have been expanded long ago
Segment<K,V> proto = ss[0];
int cap = proto.table.length;
float lf = proto.loadFactor;
int threshold = (int)(cap * lf);
// Initializes an array inside segment[k]
HashEntry<K,V>[] tab = (HashEntry<K,V>[])new HashEntry[cap];
if ((seg = (Segment<K,V>)UNSAFE.getObjectVolatile(ss, u))
== null) { // Check again whether the slot is initialized by other threads.
Segment<K,V> s = new Segment<K,V>(lf, threshold, tab);
// Use the while loop and CAS internally. After the current thread successfully sets the value or other threads successfully set the value, exit
while ((seg = (Segment<K,V>)UNSAFE.getObjectVolatile(ss, u))
== null) {
if (UNSAFE.compareAndSwapObject(ss, u, null, seg = s))
break;
}
}
}
return seg;
}
In general, ensuesegment (int k) is relatively simple. CAS is used to control concurrent operations.
Why do you want to create a while loop? If CAS fails, doesn't it mean that other threads succeed? Why do you want to judge again?
If the current thread CAS fails, the while loop here is to return the seg assignment.
Get write lock: scanAndLockForPut
As we saw earlier, when putting into a segment, we first call node = tryLock()? Null: scanAndLockForPut (key, hash, value), that is, first perform a tryLock() to quickly obtain the exclusive lock of the segment. If it fails, enter the scanAndLockForPut method to obtain the lock.
Let's specifically analyze how to control locking in this method.
private HashEntry<K,V> scanAndLockForPut(K key, int hash, V value) {
HashEntry<K,V> first = entryForHash(this, hash);
HashEntry<K,V> e = first;
HashEntry<K,V> node = null;
int retries = -1; // negative while locating node
// Cyclic lock acquisition
while (!tryLock()) {
HashEntry<K,V> f; // to recheck first below
if (retries < 0) {
if (e == null) {
if (node == null) // speculatively create node
// Go here to explain that the linked list at this position of the array is empty and has no elements
// Of course, another reason for entering here is that tryLock() fails, so concurrency exists in this slot, not necessarily in this location
node = new HashEntry<K,V>(hash, key, value, null);
retries = 0;
}
else if (key.equals(e.key))
retries = 0;
else
// Go down the list
e = e.next;
}
// If the number of retries exceeds max_ SCAN_ Restries (single core 1 multi-core 64), then do not rob, enter the blocking queue and wait for the lock
// lock() is a blocking method until it returns after obtaining the lock
else if (++retries > MAX_SCAN_RETRIES) {
lock();
break;
}
else if ((retries & 1) == 0 &&
// At this time, there is a big problem, that is, new elements enter the linked list and become a new header
// So the strategy here is to go through the scanAndLockForPut method again
(f = entryForHash(this, hash)) != first) {
e = first = f; // re-traverse if entry changed
retries = -1;
}
}
return node;
}
This method has two exits. One is that tryLock() succeeds and the loop terminates. The other is that the number of retries exceeds max_ SCAN_ Restries, go to the lock() method, which will block and wait until the exclusive lock is successfully obtained.
This method seems complex, but it actually does one thing, that is, obtain the exclusive lock of the segment, and instantiate the node if necessary.
Capacity expansion: rehash
Repeat, the segment array cannot be expanded. The expansion is to expand the capacity of the array hashentry < K, V > [] in a certain position of the segment array. After the expansion, the capacity is twice that of the original.
First of all, we need to review the place where the expansion is triggered. When putting, if it is judged that the insertion of the value will cause the number of elements of the segment to exceed the threshold, expand the capacity first and then interpolate. Readers can go back to the put method at this time.
This method does not need to consider concurrency, because when it comes here, it holds the exclusive lock of the segment.
// The node on the method parameter is the data to be added to the new array after this expansion.
private void rehash(HashEntry<K,V> node) {
HashEntry<K,V>[] oldTable = table;
int oldCapacity = oldTable.length;
// 2x
int newCapacity = oldCapacity << 1;
threshold = (int)(newCapacity * loadFactor);
// Create a new array
HashEntry<K,V>[] newTable =
(HashEntry<K,V>[]) new HashEntry[newCapacity];
// If the new mask is expanded from 16 to 32, the sizeMask is 31, corresponding to binary '000... 00011111'
int sizeMask = newCapacity - 1;
// Traverse the original array, the old routine, and split the linked list at position i of the original array into two positions i and i+oldCap of the new array
for (int i = 0; i < oldCapacity ; i++) {
// e is the first element of the linked list
HashEntry<K,V> e = oldTable[i];
if (e != null) {
HashEntry<K,V> next = e.next;
// Calculate where it should be placed in the new array,
// Assuming that the length of the original array is 16 and e is at oldTable[3], idx can only be 3 or 3 + 16 = 19
int idx = e.hash & sizeMask;
if (next == null) // There is only one element at this position, which is easier to do
newTable[idx] = e;
else { // Reuse consecutive sequence at same slot
// e is the linked list header
HashEntry<K,V> lastRun = e;
// idx is the new position of the head node e of the current linked list
int lastIdx = idx;
// The following for loop will find a lastRun node, after which all elements will be put together
for (HashEntry<K,V> last = next;
last != null;
last = last.next) {
int k = last.hash & sizeMask;
if (k != lastIdx) {
lastIdx = k;
lastRun = last;
}
}
// Put the linked list composed of lastRun and all subsequent nodes in the position of lastIdx
newTable[lastIdx] = lastRun;
// The following operations are to process the nodes before lastRun,
// These nodes may be assigned to another linked list or to the above linked list
for (HashEntry<K,V> p = e; p != lastRun; p = p.next) {
V v = p.value;
int h = p.hash;
int k = h & sizeMask;
HashEntry<K,V> n = newTable[k];
newTable[k] = new HashEntry<K,V>(h, p.key, v, n);
}
}
}
}
// Put the new node in the head of one of the two linked lists in the new array
int nodeIndex = node.hash & sizeMask; // add the new node
node.setNext(newTable[nodeIndex]);
newTable[nodeIndex] = node;
table = newTable;
}
The expansion here is more complex than the previous HashMap, and the code is a little difficult to understand. There are two for loops next to each other. What's the use of the first for?
A closer look shows that it can work without the first for loop. However, if there are more nodes behind the lastRun after the for loop, it is worth it this time. Because we only need to clone the nodes in front of lastRun, and the following series of nodes follow lastRun without any operation.
I think Doug Lea's idea is also very interesting, but the worse case is that every lastRun is the last element or very late element of the linked list, so this traversal is a bit wasteful. However, Doug lea also said that according to statistics, if the default threshold is used, only about 1 / 6 of the nodes need to be cloned.
get process analysis
Compared with put, get is really not too simple.
- Calculate the hash value and find the specific position in the segment array, or the "slot" we used earlier
- The slot is also an array. Find the specific position in the array according to the hash
- Here is the linked list. Follow the linked list to find it
public V get(Object key) {
Segment<K,V> s; // manually integrate access methods to reduce overhead
HashEntry<K,V>[] tab;
// 1. hash value
int h = hash(key);
long u = (((h >>> segmentShift) & segmentMask) << SSHIFT) + SBASE;
// 2. Find the corresponding segment according to the hash
if ((s = (Segment<K,V>)UNSAFE.getObjectVolatile(segments, u)) != null &&
(tab = s.table) != null) {
// 3. Find the linked list at the corresponding position of the internal array of segment and traverse
for (HashEntry<K,V> e = (HashEntry<K,V>) UNSAFE.getObjectVolatile
(tab, ((long)(((tab.length - 1) & h)) << TSHIFT) + TBASE);
e != null; e = e.next) {
K k;
if ((k = e.key) == key || (e.hash == h && key.equals(k)))
return e.value;
}
}
return null;
}
Concurrent problem analysis
Now that we have finished the put process and the get process, we can see that there is no lock in the get process, so naturally we need to consider the concurrency problem.
Both the put operation of adding nodes and the remove operation of deleting nodes need to add the exclusive lock on the segment, so there will be no problem between them. The problem we need to consider is that the put or remove operation occurs in the same segment during get.
-
Thread safety of put operation.
- The initialization slot, which we mentioned earlier, uses CAS to initialize the array in the Segment.
- The operation of adding nodes to the linked list is inserted into the header. Therefore, if the get operation is in the middle of the process of traversing the linked list at this time, it will not be affected. Of course, another concurrency problem is that after put, the node just inserted into the header needs to be read. This depends on the UNSAFE.putOrderedObject used in the setEntryAt method.
- Expansion. Capacity expansion is to create a new array, migrate the data, and finally set newTable to the attribute table. Therefore, if the get operation is also in progress at this time, it doesn't matter. If get goes first, it is to query the old table; If put comes first, the visibility guarantee of put operation is that table uses volatile keyword.
-
Thread safety of the remove operation.
We don't analyze the source code for the remove operation, so the readers who are interested here still need to be realistic in the source code.
The get operation needs to traverse the linked list, but the remove operation will "destroy" the linked list.
If the get operation of the remove broken node has passed, there is no problem here.
If remove destroys a node first, consider two cases. 1. If this node is a head node, you need to set the next of the head node to the element at this position of the array. Although table uses volatile decoration, volatile does not provide visibility assurance for internal operations of the array. Therefore, UNSAFE is used in the source code to operate the array. See the method setEntryAt. 2. If the node to be deleted is not the head node, it will connect the successor node of the node to be deleted to the predecessor node. The concurrency guarantee here is that the next attribute is volatile.
Java8 HashMap
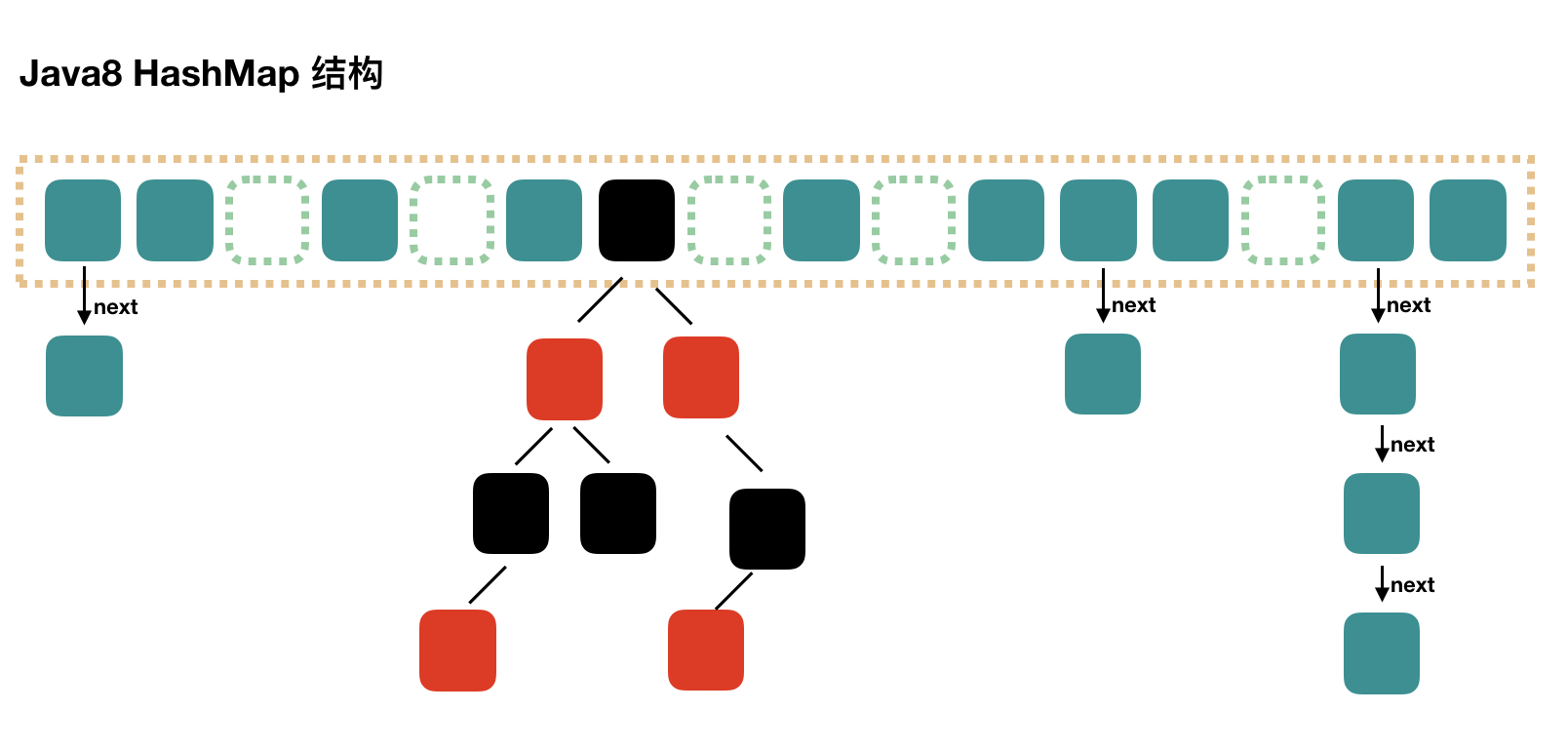
Java 8 has made some modifications to HashMap. The biggest difference is that it uses red black tree, so it is composed of array + linked list + red black tree.
According to the introduction of Java7 HashMap, we know that when searching, we can quickly locate the specific subscript of the array according to the hash value, but then we need to compare one by one along the linked list to find what we need. The time complexity depends on the length of the linked list, which is O(n).
In order to reduce the overhead of this part, in Java 8, when the number of elements in the linked list reaches 8, the linked list will be converted into a red black tree. When searching in these locations, the time complexity can be reduced to O(logN).
Let's have a simple diagram:
2
Note that the above figure is a schematic diagram, which mainly describes the structure and will not reach this state, because so much data has been expanded long ago.
Next, let's introduce it with code. Personally, the readability of Java 8's source code is worse, but it's simpler.
In Java 7, Entry is used to represent the data nodes in each HashMap. In Java 8, Node is basically the same. It has four attributes: key, value, hash and next. However, Node can only be used in the case of linked list, and TreeNode needs to be used in the case of red black tree.
We judge whether the location is a linked list or a red black tree according to whether the data type of the first Node in the array element is Node or TreeNode.
put process analysis
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
// If the fourth parameter onlyIfAbsent is true, the put operation will be performed only when the key does not exist
// The fifth parameter, evict, we don't care here
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// The first time you put a value, you will trigger the following resize(), which is similar to the first put in Java 7. You also need to initialize the array length
// The first resize is somewhat different from the subsequent expansion, because this time the array is initialized from null to the default 16 or custom initial capacity
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// Find the specific array subscript. If there is no value at this location, you can directly initialize the Node and place it at this location
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {// Array has data at this location
Node<K,V> e; K k;
// First, judge whether the key of the first data in this location is equal to the data we want to insert. If so, take out this node
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// If the node is a node representing the red black tree, call the interpolation method of the red black tree. This paper will not expand the red black tree
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
// Here, it shows that the array is a linked list at this position
for (int binCount = 0; ; ++binCount) {
// Insert to the back of the linked list (Java 7 is the front of the linked list)
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// TREEIFY_ The threshold is 8, so if the newly inserted value is the 8th in the linked list
// It will trigger the following treeifyBin, that is, convert the linked list into a red black tree
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// If an "equal" key(= = or equals) is found in the linked list
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
// At this time, break, then e is the node in the linked list [equal to the key of the new value to be inserted]
break;
p = e;
}
}
// e!=null indicates that the key with old value is "equal" to the key to be inserted
// For the put operation we analyzed, the following if is actually "value overwrite" and then returns the old value
if (e != null) {
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
// If the size of HashMap has exceeded the threshold due to the newly inserted value, it needs to be expanded
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
A little different from Java 7 is that Java 7 expands the capacity first and then inserts new values. Java 8 interpolates and then expands the capacity, but this is not important.
Array expansion
The resize() method is used to initialize the array or array expansion. After each expansion, the capacity will be twice the original and the data will be migrated.
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) { // Corresponding array expansion
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// Double the size of the array
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// Double the threshold
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // Corresponding to the first put after new HashMap(int initialCapacity) initialization
newCap = oldThr;
else {// Corresponding to the first put after initialization with new HashMap()
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
// Initializes a new array with the new array size
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab; // If you are initializing an array, this is the end, and you can return newTab
if (oldTab != null) {
// Start traversing the original array for data migration.
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
// If there is only a single element in the array position, it is simple. Simply migrate this element
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// If it's a red black tree, we won't start it
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else {
// This is the case of handling linked lists,
// You need to split the linked list into two linked lists, put them into a new array, and keep the original order
// loHead and loTail correspond to one linked list, while hiHead and hiTail correspond to another linked list. The code is relatively simple
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
// First linked list
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
// The new position of the second linked list is j + oldCap, which is well understood
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
get process analysis
Compared with put, get is really too simple.
- Calculate the hash value of the key and find the corresponding array subscript according to the hash value: hash & (length-1)
- Judge whether the element at this position of the array is exactly what we are looking for. If not, take the third step
- Judge whether the element type is a TreeNode. If so, use the red black tree method to get the data. If not, go to step 4
- Traverse the linked list until an equal (= = or equals) key is found
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// Judge whether the first node is needed
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// Judge whether it is a red black tree
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
// Linked list traversal
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
Java8 ConcurrentHashMap
To be honest, the concurrent HashMap implemented in Java 7 is relatively complex. Java 8 has made major changes to the concurrent HashMap. It is suggested that readers can refer to the changes of HashMap in Java 8 relative to that in Java 7. For concurrent HashMap, Java 8 also introduces red black tree.
To be honest, the source code of java8 concurrent HashMap is really not simple. The most difficult thing is to expand the capacity, and the data migration operation is not easy to understand.
Let's use a schematic diagram to describe its structure:
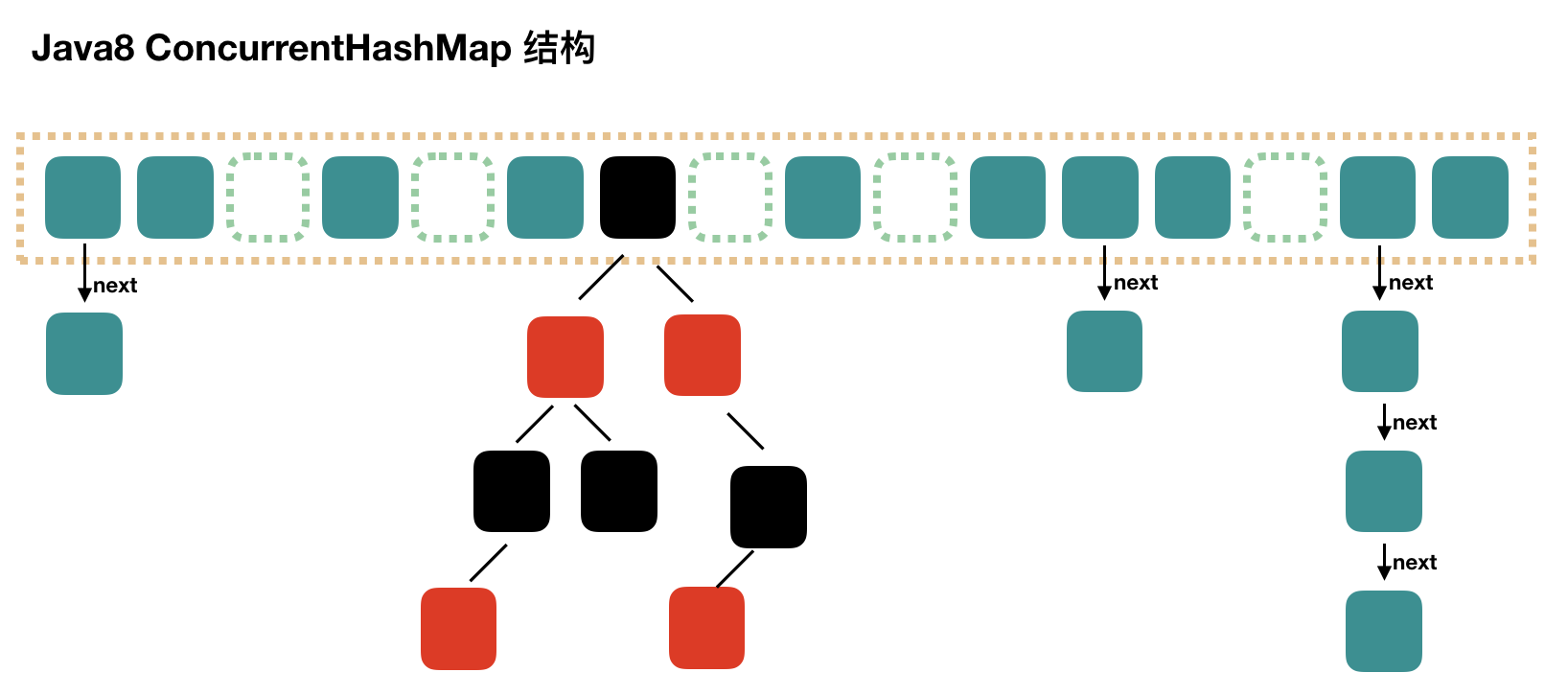
The structure is basically the same as the HashMap of Java 8, but it needs to ensure thread safety, so it really needs to be more complex in the source code.
initialization
// There's nothing to do here
public ConcurrentHashMap() {
}
public ConcurrentHashMap(int initialCapacity) {
if (initialCapacity < 0)
throw new IllegalArgumentException();
int cap = ((initialCapacity >= (MAXIMUM_CAPACITY >>> 1)) ?
MAXIMUM_CAPACITY :
tableSizeFor(initialCapacity + (initialCapacity >>> 1) + 1));
this.sizeCtl = cap;
}
This initialization method is interesting. By providing the initial capacity, sizeCtl is calculated, sizeCtl = [(1.5 * initialCapacity + 1), and then the nearest n-th power of 2 is taken upward]. If the initialCapacity is 10, the sizeCtl is 16. If the initialCapacity is 11, the sizeCtl is 32.
sizeCtl is used in many scenarios, but as long as you follow the idea of the article, you won't be confused by it.
If you like tossing, you can also take a look at another construction method with three parameters. I won't say it here. Most of the time, we will use the parameterless constructor for instantiation. Let's also analyze the source code according to this idea.
put process analysis
Take a closer look at the code line by line:
public V put(K key, V value) {
return putVal(key, value, false);
}
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
// Get hash value
int hash = spread(key.hashCode());
// Used to record the length of the corresponding linked list
int binCount = 0;
for (Node<K,V>[] tab = table;;) {
Node<K,V> f; int n, i, fh;
// If the array is empty, initialize the array
if (tab == null || (n = tab.length) == 0)
// Initialize the array, which will be described in detail later
tab = initTable();
// Find the array subscript corresponding to the hash value to get the first node f
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
// If the array is empty,
// Use a CAS operation to put the new value into it. The put operation is almost over and can be pulled to the last side
// If CAS fails, there are concurrent operations. Just go to the next cycle
if (casTabAt(tab, i, null,
new Node<K,V>(hash, key, value, null)))
break; // no lock when adding to empty bin
}
// hash can be equal to MOVED. This can only be seen later, but you can guess from the name. It must be because of capacity expansion
else if ((fh = f.hash) == MOVED)
// Help with data migration. It's easy to understand this after reading the introduction of data migration
tab = helpTransfer(tab, f);
else { // That is to say, f is the head node of this position, and it is not empty
V oldVal = null;
// Gets the monitor lock of the head node of the array at this position
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) { // The hash value of the header node is greater than 0, indicating that it is a linked list
// Used to accumulate and record the length of the linked list
binCount = 1;
// Traversal linked list
for (Node<K,V> e = f;; ++binCount) {
K ek;
// If an "equal" key is found, judge whether to overwrite the value, and then you can break
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent)
e.val = value;
break;
}
// At the end of the linked list, put the new value at the end of the linked list
Node<K,V> pred = e;
if ((e = e.next) == null) {
pred.next = new Node<K,V>(hash, key,
value, null);
break;
}
}
}
else if (f instanceof TreeBin) { // Red black tree
Node<K,V> p;
binCount = 2;
// Call the interpolation method of red black tree to insert a new node
if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
}
}
if (binCount != 0) {
// Determine whether to convert the linked list into a red black tree. The critical value is the same as HashMap, which is 8
if (binCount >= TREEIFY_THRESHOLD)
// This method is slightly different from that in HashMap, that is, it does not necessarily carry out red black tree conversion,
// If the length of the current array is less than 64, you will choose to expand the array instead of converting to a red black tree
// We won't look at the specific source code. We'll talk about it later in the expansion part
treeifyBin(tab, i);
if (oldVal != null)
return oldVal;
break;
}
}
}
//
addCount(1L, binCount);
return null;
}
After reading the main process of put, there are at least several problems left. The first is initialization, the second is capacity expansion, and the third is to help data migration. We will introduce them one by one later.
Initialization array: initTable
This is relatively simple. It mainly initializes an array of appropriate size, and then sets sizeCtl.
The concurrency problem in the initialization method is controlled by performing a CAS operation on sizeCtl.
private final Node<K,V>[] initTable() {
Node<K,V>[] tab; int sc;
while ((tab = table) == null || tab.length == 0) {
// The "credit" of initialization was "robbed" by other threads
if ((sc = sizeCtl) < 0)
Thread.yield(); // lost initialization race; just spin
// CAS, set sizeCtl to - 1, which means that the lock has been robbed
else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
if ((tab = table) == null || tab.length == 0) {
// DEFAULT_ The default initial capacity of capability is 16
int n = (sc > 0) ? sc : DEFAULT_CAPACITY;
// Initialize the array with a length of 16 or the length provided during initialization
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
// Assign this array to table, which is volatile
table = tab = nt;
// If n is 16, then sc = 12
// It's actually 0.75 * n
sc = n - (n >>> 2);
}
} finally {
// Set sizeCtl to sc, let's take it as 12
sizeCtl = sc;
}
break;
}
}
return tab;
}
Linked list to red black tree: treeifyBin
We also said in the put source code analysis earlier that treeifyBin does not necessarily carry out red black tree conversion, or it may only do array expansion. Let's do source code analysis.
private final void treeifyBin(Node<K,V>[] tab, int index) {
Node<K,V> b; int n, sc;
if (tab != null) {
// MIN_ TREEIFY_ Capability is 64
// Therefore, if the array length is less than 64, that is, 32 or 16 or less, the array capacity will be expanded
if ((n = tab.length) < MIN_TREEIFY_CAPACITY)
// We will analyze this method in detail later
tryPresize(n << 1);
// b is the head node
else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {
// Lock
synchronized (b) {
if (tabAt(tab, index) == b) {
// The following is to traverse the linked list and establish a red black tree
TreeNode<K,V> hd = null, tl = null;
for (Node<K,V> e = b; e != null; e = e.next) {
TreeNode<K,V> p =
new TreeNode<K,V>(e.hash, e.key, e.val,
null, null);
if ((p.prev = tl) == null)
hd = p;
else
tl.next = p;
tl = p;
}
// Set the red black tree to the corresponding position of the array
setTabAt(tab, index, new TreeBin<K,V>(hd));
}
}
}
}
}
Capacity expansion: tryprevize
If the source code of java8 concurrent HashMap is not simple, it means capacity expansion and migration.
To fully understand this method, you also need to look at the subsequent transfer method. Readers should know this in advance.
The capacity expansion here is also doubled. After expansion, the array capacity is twice that of the original.
// First of all, the method parameter size has doubled when it is passed in
private final void tryPresize(int size) {
// c: 1.5 times the size, plus 1, and then take the nearest 2 to the nth power.
int c = (size >= (MAXIMUM_CAPACITY >>> 1)) ? MAXIMUM_CAPACITY :
tableSizeFor(size + (size >>> 1) + 1);
int sc;
while ((sc = sizeCtl) >= 0) {
Node<K,V>[] tab = table; int n;
// The if branch is basically the same as the code for initializing the array. Here, we can ignore this code
if (tab == null || (n = tab.length) == 0) {
n = (sc > c) ? sc : c;
if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
try {
if (table == tab) {
@SuppressWarnings("unchecked")
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
table = nt;
sc = n - (n >>> 2); // 0.75 * n
}
} finally {
sizeCtl = sc;
}
}
}
else if (c <= sc || n >= MAXIMUM_CAPACITY)
break;
else if (tab == table) {
// I don't understand what rs really means, but it doesn't matter
int rs = resizeStamp(n);
if (sc < 0) {
Node<K,V>[] nt;
if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
transferIndex <= 0)
break;
// 2. Add 1 to sizeCtl with CAS, and then execute the transfer method
// nextTab is not null at this time
if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
transfer(tab, nt);
}
// 1. Set sizeCtl to (RS < < resize_stamp_shift) + 2)
// I don't understand what this value really means? But what you can calculate is that the result is a relatively large negative number
// Call the transfer method, and the nextTab parameter is null
else if (U.compareAndSwapInt(this, SIZECTL, sc,
(rs << RESIZE_STAMP_SHIFT) + 2))
transfer(tab, null);
}
}
}
The core of this method is the operation of sizecl value. First set it to a negative number, then execute transfer(tab, null), and then add sizecl by 1 and execute transfer(tab, nt) in the next cycle. Then, you may continue to add sizecl by 1 and execute transfer(tab, nt).
Therefore, the possible operation is to execute transfer(tab, null) + multiple transfers (tab, NT). How to end the cycle here needs to read the transfer source code.
Data migration: transfer
The following method is a little long. Migrate the elements of the original tab array to the new nextTab array.
Although the multiple calls to transfer in the tryprevize method we mentioned earlier do not involve multithreading, this transfer method can be called in other places. Typically, we said before talking about the put method. Please look up to see if there is a place where the helpTransfer method is called, and the helpTransfer method will call the transfer method.
This method supports multi-threaded execution. When the peripheral calls this method, it will ensure that the nextTab parameter of the first thread initiating data migration is null. When this method is called later, nextTab will not be null.
Before reading the source code, you should understand the mechanism of concurrent operation. The length of the original array is n, so we have n migration tasks. It is easiest for each thread to be responsible for one small task at a time. After each task is completed, we can detect whether there are other unfinished tasks to help with migration. Doug Lea uses a string. The simple solution is the step size. Each thread is responsible for migrating part of it each time, For example, 16 small tasks are migrated each time. Therefore, we need a global scheduler to arrange which thread performs which tasks. This is the function of the property transferIndex.
The first thread initiating data migration will point the transferIndex to the last position of the original array, then the backward and forward stripe tasks belong to the first thread, then point the transferIndex to the new position, and the forward stripe tasks belong to the second thread, and so on. Of course, the second thread mentioned here does not really refer to the second thread, or it can be the same thread. This reader should be able to understand it. In fact, a large migration task is divided into task packages.
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
int n = tab.length, stride;
// Stripe is directly equal to N in single core mode, and (n > > > 3) / ncpu in multi-core mode. The minimum value is 16
// Stripe can be understood as "step size". There are n locations that need to be migrated,
// Divide the n tasks into multiple task packages, and each task package has stripe tasks
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
stride = MIN_TRANSFER_STRIDE; // subdivide range
// If nextTab is null, initialize it first
// As we said earlier, the periphery will ensure that the parameter nextTab is null when the first thread initiating migration calls this method
// When the thread participating in the migration calls this method later, nextTab will not be null
if (nextTab == null) {
try {
// Capacity doubled
Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1];
nextTab = nt;
} catch (Throwable ex) { // try to cope with OOME
sizeCtl = Integer.MAX_VALUE;
return;
}
// nextTable is an attribute in ConcurrentHashMap
nextTable = nextTab;
// transferIndex is also an attribute of ConcurrentHashMap, which is used to control the location of migration
transferIndex = n;
}
int nextn = nextTab.length;
// ForwardingNode is translated as the Node being migrated
// This construction method will generate a Node. The key, value and next are null. The key is that the hash is MOVED
// We will see later that after the node at position i in the original array completes the migration,
// The ForwardingNode will be set at location i to tell other threads that the location has been processed
// So it's actually a sign.
ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
// advance means that you are ready to move to the next location after completing the migration of one location
boolean advance = true;
boolean finishing = false; // to ensure sweep before committing nextTab
/*
* The following for loop is the most difficult to understand in the front. To understand them, you should first understand the back, and then look back
*
*/
// i is the location index, and bound is the boundary. Note that it is from back to front
for (int i = 0, bound = 0;;) {
Node<K,V> f; int fh;
// The following while is really hard to understand
// If advance is true, it means that the next location can be migrated
// Simply understand the ending: i points to transferIndex, and bound points to transferIndex stripe
while (advance) {
int nextIndex, nextBound;
if (--i >= bound || finishing)
advance = false;
// Assign the transferIndex value to nextIndex
// Here, once the transferIndex is less than or equal to 0, it means that there are corresponding threads to process all positions of the original array
else if ((nextIndex = transferIndex) <= 0) {
i = -1;
advance = false;
}
else if (U.compareAndSwapInt
(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ?
nextIndex - stride : 0))) {
// Look at the code in parentheses. nextBound is the boundary of this migration task. Note that it is from back to front
bound = nextBound;
i = nextIndex - 1;
advance = false;
}
}
if (i < 0 || i >= n || i + n >= nextn) {
int sc;
if (finishing) {
// All migration operations have been completed
nextTable = null;
// Assign the new nextTab to the table attribute to complete the migration
table = nextTab;
// Recalculate sizeCtl: n is the length of the original array, so the value obtained by sizeCtl will be 0.75 times the length of the new array
sizeCtl = (n << 1) - (n >>> 1);
return;
}
// As we said before, sizeCtl will be set to (RS < < resize_stamp_shift) + 2 before migration
// Then, for each thread participating in the migration, sizeCtl will be increased by 1,
// Here, the CAS operation is used to subtract 1 from sizeCtl, which means that your task has been completed
if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
// The task ends and the method exits
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
return;
// Here, the description (SC - 2) = = resizestamp (n) < < resize_ STAMP_ SHIFT,
// In other words, after all the migration tasks are completed, it will enter the if(finishing) {} branch above
finishing = advance = true;
i = n; // recheck before commit
}
}
// If the location i is empty and there are no nodes, the "ForwardingNode" empty node just initialized is placed“
else if ((f = tabAt(tab, i)) == null)
advance = casTabAt(tab, i, null, fwd);
// At this location is a ForwardingNode, which means that the location has been migrated
else if ((fh = f.hash) == MOVED)
advance = true; // already processed
else {
// Lock the node at this position of the array and start processing the migration at this position of the array
synchronized (f) {
if (tabAt(tab, i) == f) {
Node<K,V> ln, hn;
// If the hash of the head Node is greater than 0, it indicates that it is the Node node of the linked list
if (fh >= 0) {
// The following is similar to the concurrent HashMap migration in Java 7,
// You need to divide the linked list into two,
// Find the lastRun in the original linked list, and then migrate the lastRun and its subsequent nodes together
// Nodes before lastRun need to be cloned and then divided into two linked lists
int runBit = fh & n;
Node<K,V> lastRun = f;
for (Node<K,V> p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
if (runBit == 0) {
ln = lastRun;
hn = null;
}
else {
hn = lastRun;
ln = null;
}
for (Node<K,V> p = f; p != lastRun; p = p.next) {
int ph = p.hash; K pk = p.key; V pv = p.val;
if ((ph & n) == 0)
ln = new Node<K,V>(ph, pk, pv, ln);
else
hn = new Node<K,V>(ph, pk, pv, hn);
}
// One of the linked lists is placed in the position i of the new array
setTabAt(nextTab, i, ln);
// Another linked list is placed in the position i+n of the new array
setTabAt(nextTab, i + n, hn);
// Set the position of the original array to fwd, which means that the position has been processed,
// Once other threads see that the hash value of this location is MOVED, they will not migrate
setTabAt(tab, i, fwd);
// If advance is set to true, it means that the location has been migrated
advance = true;
}
else if (f instanceof TreeBin) {
// Migration of red and black trees
TreeBin<K,V> t = (TreeBin<K,V>)f;
TreeNode<K,V> lo = null, loTail = null;
TreeNode<K,V> hi = null, hiTail = null;
int lc = 0, hc = 0;
for (Node<K,V> e = t.first; e != null; e = e.next) {
int h = e.hash;
TreeNode<K,V> p = new TreeNode<K,V>
(h, e.key, e.val, null, null);
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p;
else
loTail.next = p;
loTail = p;
++lc;
}
else {
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
++hc;
}
}
// If the number of nodes is less than 8 after one is divided into two, the red black tree will be converted back to the linked list
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
(hc != 0) ? new TreeBin<K,V>(lo) : t;
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
(lc != 0) ? new TreeBin<K,V>(hi) : t;
// Place ln in position i of the new array
setTabAt(nextTab, i, ln);
// Place hn at position i+n of the new array
setTabAt(nextTab, i + n, hn);
// Set the position of the original array to fwd, which means that the position has been processed,
// Once other threads see that the hash value of this location is MOVED, they will not migrate
setTabAt(tab, i, fwd);
// If advance is set to true, it means that the location has been migrated
advance = true;
}
}
}
}
}
}
In the final analysis, the transfer method does not implement all migration tasks. Each time this method is called, it only implements the migration of the transferIndex to the previous stripe, and the rest needs to be controlled by the periphery.
At this time, it may be clearer to go back and take a closer look at the tryprevize method.
get process analysis
The get method is always the simplest, and here is no exception:
- Calculate hash value
- Find the corresponding position of the array according to the hash value: (n - 1) & H
- Search according to the properties of the node at this location
- If the location is null, you can return null directly
- If the node at this location is exactly what we need, return the value of this node
- If the hash value of the node at this location is less than 0, it indicates that the capacity is being expanded, or it is a red black tree. We will introduce the find method later
- If the above three items are not satisfied, it is a linked list. You can traverse and compare them
public V get(Object key) {
Node<K,V>[] tab; Node<K,V> e, p; int n, eh; K ek;
int h = spread(key.hashCode());
if ((tab = table) != null && (n = tab.length) > 0 &&
(e = tabAt(tab, (n - 1) & h)) != null) {
// Determine whether the head node is the node we need
if ((eh = e.hash) == h) {
if ((ek = e.key) == key || (ek != null && key.equals(ek)))
return e.val;
}
// If the hash of the head node is less than 0, it indicates that the capacity is being expanded, or the location is a red black tree
else if (eh < 0)
// Refer to ForwardingNode.find(int h, Object k) and TreeBin.find(int h, Object k)
return (p = e.find(h, key)) != null ? p.val : null;
// Traversal linked list
while ((e = e.next) != null) {
if (e.hash == h &&
((ek = e.key) == key || (ek != null && key.equals(ek))))
return e.val;
}
}
return null;
}
To put it simply, most of the contents of this method are very simple. Only in the case of capacity expansion, ForwardingNode.find(int h, Object k) is a little more complex. However, after understanding the data migration process, it is not difficult, so it is not discussed here due to space limitations.