Problem surface

Given a sequence. Query the maximum sum of sub segments whose left endpoint is between [x1, y1] [x1, y1], and right endpoint is between [X2, y2] [X2, y2], and ensure that the data is x1 ≤ x2,y1 ≤ y2 x_ \ Leq x_, y1 \ Leq y x1 ≤ x2,y1 ≤ y2, but do not guarantee that the interval where the endpoint is not coincident.

Title Solution

It's better to do the line tree first. SP1043 GSS1 - Can you answer these queries I

First of all, it is found that [y1+1,x2 − 1][y1+1,x2-1][y1+1,x2 − 1] is the required interval.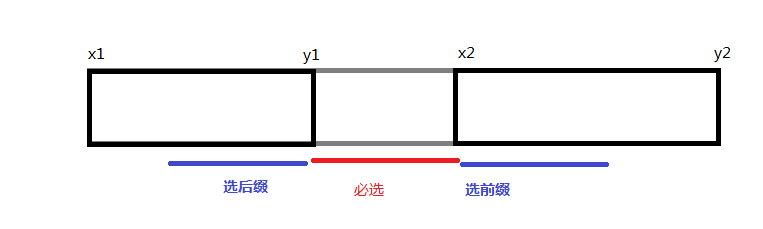

Then analyze the intersection of two line segments: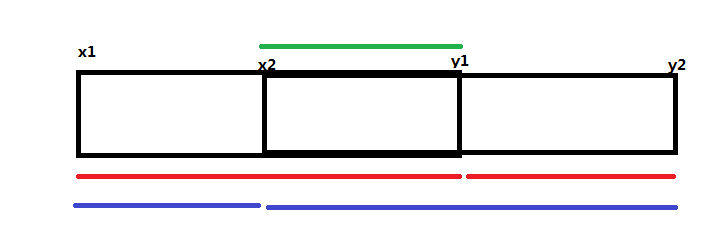

There are three situations

• The endpoint is at [x2,y1][x2,y1][x2,y1], and only the maximum value of [x2,y1][x2,y1][x2,y1] interval sub segment is calculated.
• The left endpoint is at [x1,x2 − 1][x1,x2-1][x1,x2 − 1], the right endpoint is at [x2,y2][x2,y2][x2,y2], which is calculated according to the method of line segment separation.
• The left endpoint is at [x1,y1][x1,y1][x1,y1], the right endpoint is at [x1+1,y2][x1+1,y2][x1+1,y2], similarly

p.s.p.s.p.s. maybe cmathcmath does not support Y1 Y1 Y1. I changed x1, Y1, X2, y2x1, y2x1, Y1, X2, Y2 into L1, R1, L2, r2l1, R1, R2, R2.

#include <bits/stdc++.h>
#define MAXN 50005
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while (ch<'0'||ch>'9'){
        if (ch=='-') f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9'){
        x=(x<<3)+(x<<1)+(ch^'0');
        ch=getchar();
    }
    return x*f;
}
int a[MAXN];
namespace SegmentTree{
    struct node{
        int l,r;
        int lmax,rmax,maxn;//Maximum value from left end, maximum value from right end, maximum value of the whole section
        int val;//The sum of this paragraph
    }tree[MAXN<<2];
    node empty_node(){
        node temp;
        temp.l=temp.r=temp.lmax=temp.rmax=temp.maxn=temp.val=0;
        return temp;
    }
    void Init(){
        memset(tree,0,sizeof(tree));
    }
    #define lc i<<1
    #define rc i<<1|1
    node operator + (node A,node B){
        node temp;
        temp.lmax=max(B.lmax+A.val,A.lmax);
        temp.rmax=max(A.rmax+B.val,B.rmax);
        temp.maxn=max(max(A.maxn,B.maxn),A.rmax+B.lmax);
        temp.val=A.val+B.val;
        temp.l=A.l,temp.r=B.r;
        return temp;
    }
    void pushup(int i){
        tree[i]=tree[lc]+tree[rc];
    }
    void Build(int l,int r,int i){
        if (l==r){
            tree[i].lmax=tree[i].rmax=tree[i].maxn=tree[i].val=a[l];
            tree[i].l=tree[i].r=l;
            return ;
        }
        int mid=(l+r)>>1;
        Build(l,mid,lc);
        Build(mid+1,r,rc);
        pushup(i);
    }
    node TEMPQuery(int L,int R,int i){
        if (L>R) return empty_node();//Special judgment l > R
        if (L<=tree[i].l&&tree[i].r<=R){
            return tree[i];
        }
        int mid=(tree[i].l+tree[i].r)>>1;
        if (L>mid) return TEMPQuery(L,R,rc);
        else if (R<=mid) return TEMPQuery(L,R,lc);
        else return TEMPQuery(L,R,lc)+TEMPQuery(L,R,rc);
    }
    node Query(int L,int R){
        return TEMPQuery(L,R,1);
    }
};
using namespace SegmentTree;
inline int Get_Ans(int l1,int r1,int l2,int r2){//R1 < = L2, i.e. interval [l1,r1],[l2,r2] is separated or tangent
    if (r1==l2) return Query(l1,r1).rmax+Query(l2,r2).lmax-a[r1];//Tangent special case
    return Query(l1,r1).rmax+Query(r1+1,l2-1).val+Query(l2,r2).lmax;
}
inline int Solve(int l1,int r1,int l2,int r2){
    if (l1==l2&&r1==r2){
        return Query(l1,r1).maxn;
    }
    if (r1<l2){
        return Get_Ans(l1,r1,l2,r2);
    }
    else {
        int ans=Query(l2,r1).maxn;
        ans=max(ans,Get_Ans(l1,l2,l2,r2));
        ans=max(ans,Get_Ans(l1,r1,r1,r2));
        return ans;
    }
}
int main(){
    int Case=read();
    for (register int k=1;k<=Case;++k){
        int n=read();
        for (register int i=1;i<=n;++i){
            a[i]=read();
        }
        Init();
        Build(1,n,1);
        int q=read();
        while (q--){
            int l1=read(),r1=read(),l2=read(),r2=read();
            printf("%d\n",Solve(l1,r1,l2,r2));
        }
    }
}