Recently, I studied Sudoku and other issues (in fact, there are only two). To sum up:
Sudoku is regarded as a kind of mental work because of its complex relationship. If we want to solve this problem with computers, it is regarded as a violent problem.
For these relationships, we can use several two-dimensional arrays to store them.
For example, in P1784 Sudoku, we only need to use an array \ (h_{i,num} \) to indicate whether the \ (i \) row can put \ (num \) numbers, an array \ (l_{i,num} \) to indicate whether the \ (i \) column can put \ (num \) numbers, and then use a \ (g_{i,num} \) to indicate whether the \ (i \) ninth house can put \ (num \) numbers.
In fact, before looking at the solution, I used a three-dimensional array to describe the relationship between placement and non placement. I used \ (B {I, J, num} \) to indicate whether it is possible to place \ (num \) at the position of \ ((i,j) \). Why is this method not good. After careful thinking, you will find that a \ (b_{i,j,num} \) is related to its rows and columns. Therefore, there are many places to change this data. When I go back, I don't know if I changed this one, so this method is not very good. At the same time, this method is cumbersome for marking the Jiugong grid one by one.
OK, after the theoretical part, let's start the practical part.
Start with a yellow question. Title portal
Directly, Sudoku.
With a fluke attitude, I didn't write optimization. Directly, the result is AC. in fact, this problem doesn't need optimization.
OK, go straight to the die Code:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
const int n=9;
int h[11][11],l[11][11],g[11][11],a[11][11];
inline int gg(int x,int y){
return (x-1)/3*3+(y-1)/3+1;
}
void Print(){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j)
cout<<a[i][j]<<' ';
cout<<endl;
}
exit(0);
}
void dfs(int x,int y){
if(x>n) dfs(1,y+1);
if(y>n){
Print();
exit(0);
}
if(a[x][y]){
dfs(x+1,y);
return;
}
for(int num=1;num<=9;++num){
if(h[x][num]&&l[y][num]&&g[gg(x,y)][num]){
a[x][y]=num;
h[x][num]=l[y][num]=g[gg(x,y)][num]=0;
dfs(x+1,y);
h[x][num]=l[y][num]=g[gg(x,y)][num]=1;
a[x][y]=0;
}
}
}
int main(){
memset(h,1,sizeof(h));
memset(l,1,sizeof(l));
memset(g,1,sizeof(g));
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
cin>>a[i][j];
if(a[i][j]!=0) h[i][a[i][j]]=l[j][a[i][j]]=g[gg(i,j)][a[i][j]]=0;
}
dfs(1,1);
return 0;
}
//(x-1)/3*3+(y-1)/3+1
This problem only requires finding the only solution that meets the conditions, so the time complexity is not so false. The procedure may be terminated midway\ (79ms \) it's actually very fast.
According to this idea, we can slightly adjust the search order along with the urine idea of the questioner. It turns out that the thinking for each person is from 1 to 9, so I come in the opposite direction, from 9 to 1.
In fact, the random data can't be optimized at all, but there are more optimization problems. One point optimized for 50ms
Total \ (21ms \).
OK, now let's go to the second question, step by step. Let's have a blue question on the second question: Title portal
In fact, I feel it is very difficult.
For this question, we only need to search it out, and then take a maximum value according to the answer. But pruning, as well as the thinking of search order, should be considered completely. This problem feels that there is no optimality pruning, so it is mainly optimized from the search order.
No optimization
This method is simple, that is, the weighted answer version of the previous question. But I passed this question (very reluctantly).
Not much to say, go directly to the die Code:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
inline int gg(int x,int y){
return (x-1)/3*3+(y-1)/3+1;
}
bool h[11][11],l[11][11],g[11][11];
vector<int>p;
const int n=9;
int a[11][11];
int ans=0;
int xs[11][11]={{0,0,0,0,0,0,0,0,0,0},{0,6,6,6,6,6,6,6,6,6},{0,6,7,7,7,7,7,7,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,9,10,9,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,7,7,7,7,7,7,6},{0,6,6,6,6,6,6,6,6,6}};
void dfs(int x,int y,int score){
if(x>n) dfs(1,y+1,score);
if(y>n){
ans=max(score,ans);
return;
}
if(a[x][y]){dfs(x+1,y,score+a[x][y]*xs[x][y]);
return;}
for(register int num=1;num<=9;++num)
if(h[x][num]&&l[y][num]&&g[gg(x,y)][num]){
//This indicates that this bit can be put with num
h[x][num]=l[y][num]=g[gg(x,y)][num]=0;
dfs(x+1,y,score+num*xs[x][y]);
h[x][num]=l[y][num]=g[gg(x,y)][num]=1;
}
}
int main(){
memset(h,1,sizeof(h));
memset(l,1,sizeof(l));
memset(g,1,sizeof(g));
for(register int i=1;i<=n;++i)
for(register int j=1;j<=n;++j){
read(a[i][j]);
h[i][a[i][j]]=l[j][a[i][j]]=g[gg(i,j)][a[i][j]]=(a[i][j]==0);
}
dfs(1,1,0);
cout<<((ans==0)?-1:ans)<<endl;
return 0;
}
//(x-1)/3*3+(y-1)/3+1
This method runs very slowly, almost TLE Evaluation record
Way1 row optimization
This one has a lot of thinking points.
Why is this optimization optimized. Many Valley people have raised this question. After a period of research, I have come to the reason.
If I say, now I just need to fill in a \ (3 × 3 \), as shown below.
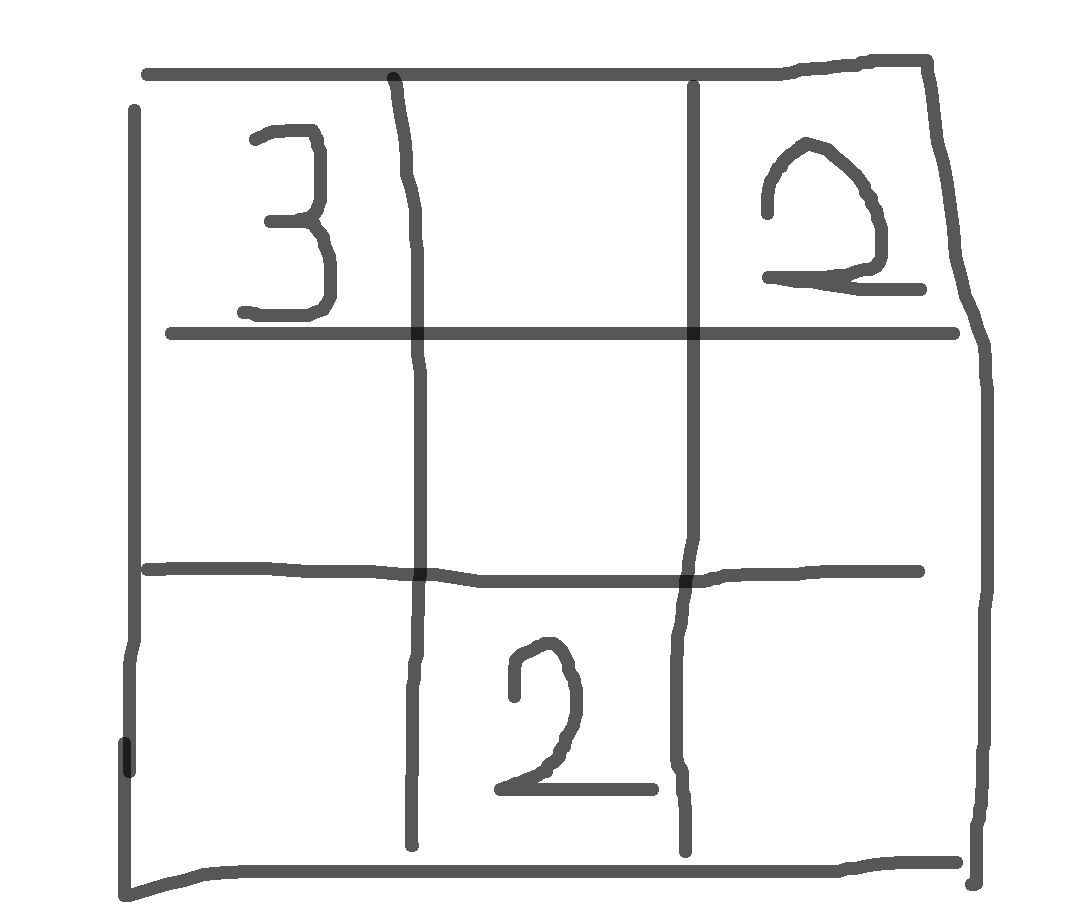
OK, now in this diagram, the point with the least number must be the first line. If I fill it in now, the second point in the second line can also be determined. Therefore, this idea is relatively fast.
The main misunderstanding is that we should consider it from the perspective of filling in this Sudoku, not from the perspective of score.
Therefore, this algorithm is relatively fast (\ (966ms \)).
It is worth mentioning that I also used the method of the above question (changing the search order) to try. In fact, it is slower (\ (977ms \). It will not slow down according to reason. It may be the fluctuation of evaluation. However, in fact, at the end of all the search, the change of search order is useless.
The following is the upper die Code:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
inline int gg(int x,int y){
return (x-1)/3*3+(y-1)/3+1;
}
struct Info{
int x,s;
bool operator <(const Info &info) const {
return s<info.s;
}
};
bool h[11][11],l[11][11],g[11][11];
const int n=9;
int a[11][11];
vector<Info>p;
int ans=0;
int xs[11][11]={{0,0,0,0,0,0,0,0,0,0},{0,6,6,6,6,6,6,6,6,6},{0,6,7,7,7,7,7,7,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,9,10,9,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,7,7,7,7,7,7,6},{0,6,6,6,6,6,6,6,6,6}};
void dfs(int x,int y,int score,int dep){
if(y>n) dfs(p[dep+1].x,1,score,dep+1);
if(dep==9){
ans=max(ans,score);
return;
}
if(a[x][y]){
dfs(x,y+1,score+a[x][y]*xs[x][y],dep);
return;
}
for(register int num=1;num<=9;++num)
if(h[x][num]&&l[y][num]&&g[gg(x,y)][num]){
//This indicates that this bit can be put with num
h[x][num]=0;l[y][num]=0;g[gg(x,y)][num]=0;
dfs(x,y+1,score+num*xs[x][y],dep);
h[x][num]=1;l[y][num]=1;g[gg(x,y)][num]=1;
}
}
int main(){
memset(h,1,sizeof(h));
memset(l,1,sizeof(l));
memset(g,1,sizeof(g));
for(register int i=1;i<=n;++i)
for(register int j=1;j<=n;++j){
read(a[i][j]);
h[i][a[i][j]]=l[j][a[i][j]]=g[gg(i,j)][a[i][j]]=(a[i][j]==0);
}
for(register int i=1;i<=n;++i){
int sum=0;
for(register int j=1;j<=n;++j){
for(register int k=1;k<=n;++k)
if(h[i][k]&&l[j][k]&&g[gg(i,j)][k]) ++sum;
}
p.push_back({i,sum});
}
sort(p.begin(),p.end());
dfs(p[0].x,1,0,0);
cout<<((ans==0)?-1:ans)<<endl;
return 0;
}
//(x-1)/3*3+(y-1)/3+1
Way2: start searching where there are few methods to fill in when entering
Note that this method is not a positive solution, TLE90pts
This method is very fake. Let's talk about why it is fake. First of all, this method is not dynamic, that is to say, I have fewer filling methods at the beginning, which does not mean that there will be fewer filling methods later, so this method is not very good.
Moreover, this method is actually similar to random search, plus the constant processed at the beginning, which is actually a wrong solution.
Show me the die code here for thinking only.
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
inline int gg(int x,int y){
return (x-1)/3*3+(y-1)/3+1;
}
struct Info{
int x,y,s;
bool operator <(const Info &info) const {
return s<info.s;
}
};
bool h[11][11],l[11][11],g[11][11];
const int n=9;
int a[11][11];
vector<Info>p;
int ans=0;
int xs[11][11]={{0,0,0,0,0,0,0,0,0,0},{0,6,6,6,6,6,6,6,6,6},{0,6,7,7,7,7,7,7,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,9,10,9,8,7,6},{0,6,7,8,9,9,9,8,7,6},{0,6,7,8,8,8,8,8,7,6},{0,6,7,7,7,7,7,7,7,6},{0,6,6,6,6,6,6,6,6,6}};
void dfs(int score,int dep){
if(dep==81){
ans=max(ans,score);
return;
}
int x=p[dep].x,y=p[dep].y;
if(a[x][y]){dfs(score+a[x][y]*xs[x][y],dep+1);
return;}
for(register int num=1;num<=9;++num)
if(h[x][num]&&l[y][num]&&g[gg(x,y)][num]){
//This indicates that this bit can be put with num
h[x][num]=0;l[y][num]=0;g[gg(x,y)][num]=0;
dfs(score+num*xs[x][y],dep+1);
h[x][num]=1;l[y][num]=1;g[gg(x,y)][num]=1;
}
}
int main(){
memset(h,1,sizeof(h));
memset(l,1,sizeof(l));
memset(g,1,sizeof(g));
for(register int i=1;i<=n;++i)
for(register int j=1;j<=n;++j){
read(a[i][j]);
h[i][a[i][j]]=l[j][a[i][j]]=g[gg(i,j)][a[i][j]]=(a[i][j]==0);
}
for(register int i=1;i<=n;++i){
for(register int j=1;j<=n;++j){
int sum=0;
for(register int k=1;k<=n;++k)
if(h[i][k]&&l[j][k]&&g[gg(i,j)][k]) ++sum;
p.push_back({i,j,sum});
}
}
sort(p.begin(),p.end());
dfs(0,0);
cout<<((ans==0)?-1:ans)<<endl;
return 0;
}
//(x-1)/3*3+(y-1)/3+1