Well, first of all, the key framework of tree dp.
void dfs(int u,int fa){
///Do something
for(int i=0;i<a[u].size();++i){
//Do something
int v=a[u][i];
if(v==fa) continue;
//Do something
}
return;
}
This framework is really useful.
The main relationship of tree dp is to deal with the relationship between a node and what his son requires.
Try some questions!
Tree diameter (simplified version)
Title Description
Little Q has recently learned some knowledge of graph theory. According to the textbook, there are the following definitions. Tree: a connected undirected graph without loops. Each edge has a positive integer weight to represent its length. If a tree has \ (N \) nodes, it can be proved that it has only \ (N-1 \) edges. Path: there is at most one simple path between any two nodes in a tree. We use \ (dis(a,b) \) to represent the sum of the lengths of each side on the path of point \ (a \) and point \ (B \). Call \ (dis(a,b) \) the distance between two nodes of \ (a,b \).
Diameter: on a tree, the longest path is the diameter of the tree. The diameter of the tree may not be unique.
Now little Q wants to know, for a given tree, what is the length of its diameter? (and how many edges satisfy that all diameters pass through this edge, which does not need to be calculated for consideration)
Input format
The first line contains an integer \ (N \) indicating the number of nodes.
The next \ (N-1 \) line has three integers \ (a, b, c \) in each line, indicating that there is an undirected edge with length c between point \ (a \) and point \ (b \).
Output format
One integer per line represents the length of the diameter.
Data range and tips
For 100% test data: \ (2\leq N\leq 200000 \), \ (\ forall a,b,c \in [1,N] \)
The weight of the edge \ (\ leq 10^9 \).
sample input
6
3 1 1000
1 4 10
4 2 100
4 5 50
4 6 100
sample output
1110
Example description
There are two diameters, a 3 to 2 path and a 3 to 6 path. Both diameters pass through edges (3, 1) and edges (1, 4).
thinking
Template questions, tree diameter.
Consider that \ (f[u] \) represents the longest chain below the point of \ (U \).
Now consider how to answer the second question, although he didn't ask for an answer. How many diameters are there? Now I'll save a maximum value and judge how many times the maximum value has been updated.
Upper die Code:
#include <bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
long long dis[314514],n,m;
char ch;
vector<pair<int,int> >a[314514];
long long ans;
void dfs(int u,int fa){
for(int i=0;i<a[u].size();++i){
int v=a[u][i].first;
if(v==fa) continue;
dfs(v,u);
ans=max(ans,a[u][i].second+dis[v]+dis[u]);
dis[u]=max(dis[v]+a[u][i].second,dis[u]);
}
}
int main(){
cin>>n;
for(int i=1;i<n;++i){
int x,y,w;
read(x,y,w);
a[x].push_back(make_pair(y,w));
a[y].push_back(make_pair(x,w));
}
dfs(1,-1);
cout<<ans<<endl;
return 0;
}
Computer network
Title Description
A school bought the first computer (the number of this computer is 1) a few years ago. In recent years, the school has purchased \ (N-1 \) computers, and each new computer is connected to a previous computer. The school administrator wants to know the distance \ (S_i \) from each computer I to the computer furthest away from it. You need to provide this information.
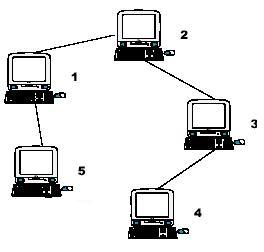
Hint: the sample input is shown in the figure above. You can know from the figure that computer 4 is the farthest from computer 1, so \ (S_1=3 \). Computer 4 and computer 5 are the farthest from computer 2, so \ (S_2=2 \). Computer 5 is the farthest from computer 3, so \ (S_3=3 \). And so on \ (S_4=4 \), \ (S_5=4 \).
Input format
The first line contains an integer \ (N\) (\(N\leq 10000 \));
The next \ (N-1 \) line describes each computer. Line \ (i \) contains two integers \ (y,l \) separated by spaces, indicating that the computer \ (i \) is connected with the previous computer \ (Y \) at a distance of L.
The sum of all \ (l \) shall not exceed \ (10 ^ 9 \).
Output format
For each set of test data output \ (N \) line, line \ (I \) indicates the longest distance \ (S_i \) from computer \ (I \).
sample input
5
1 1
2 1
3 1
1 1
sample output
3
2
3
4
4
thinking
This topic uses what I think is a clever conclusion, which was also mentioned when talking about the diameter of trees.
The original tree diameter, from a point to its farthest point, and then from that farthest point to the farthest point relative to it.
What does this mean? A point to its farthest point must be at the end of the diameter of the tree.
Then it's easy to do. Use dfs three times directly. Find one endpoint for the first time and two endpoints for the second time. By the way, record the distance from the first endpoint to all points, record the distance from the second endpoint to all points for the third time, and finally take a maximum value from the two distances.
Konjac die Code:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
int n;
int dis[114514];
int dis1[114514];
vector<pair<int,int> >a[114514];
void dfs(int u,int fa){
for(int i=0;i<a[u].size();++i){
int v=a[u][i].first;
if(v==fa) continue;
dis[v]=dis[u]+a[u][i].second;
dfs(v,u);
}
}
void dfs1(int u,int fa){
for(int i=0;i<a[u].size();++i){
int v=a[u][i].first;
if(v==fa) continue;
dis1[v]=dis1[u]+a[u][i].second;
dfs1(v,u);
}
}
int main(){
cin>>n;
for(int i=2;i<=n;++i){
int x,y;
read(x,y);
a[i].push_back(make_pair(x,y));
a[x].push_back(make_pair(i,y));
}
dfs(1,-1);
int maxn=0,maxnum=0;
for(int i=1;i<=n;++i)
if(dis[i]>maxn){
maxn=dis[i];
maxnum=i;
}
dfs1(maxnum,-1);
maxn=0,maxnum=0;
for(int i=1;i<=n;++i)
if(dis1[i]>maxn){
maxn=dis1[i];
maxnum=i;
}
memset(dis,0,sizeof(dis));
dfs(maxnum,-1);
for(int i=1;i<=n;++i)
cout<<max(dis[i],dis1[i])<<endl;
return 0;
}
Hospital settings
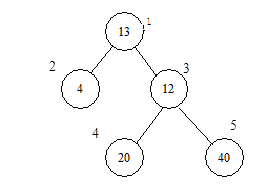
Title Description
There is a binary tree (as shown in the figure, the number in the circle represents the population of residents in the node, and the number on the edge of the circle represents the node number. Now it is required to establish a hospital on a node to minimize the sum of the distances traveled by all residents. At the same time, it is agreed that the distance between adjacent nodes is 1. In this figure, if the hospital is built at 1, the sum of distances = 4 + 12 + 220 + 240 = 136; if the hospital is built at 3 , then the distance sum = 4 * 2 + 13 + 20 + 40 = 81
Input format
The first line contains an integer \ (n \), indicating the number of nodes in the tree (\ (n\leq 100 \)). The next \ (n \) line describes the status of a node, including three integers, with spaces (one or more) between integers The first number is the number of residents; the second number is the left link, 0 means no link; the third number is the right link, 0 means no link.
Output format
An integer representing the minimum distance and.
sample input
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
sample output
81
thinking
The amount of data in this question is not very large, only 100. Now I can calculate the answer directly with Floyd algorithm, but if my data is \ (1 \times 10^6 \), I must use my method of \ (O(n) \)
First of all, if I have determined the location of the hospital and calculated the results.
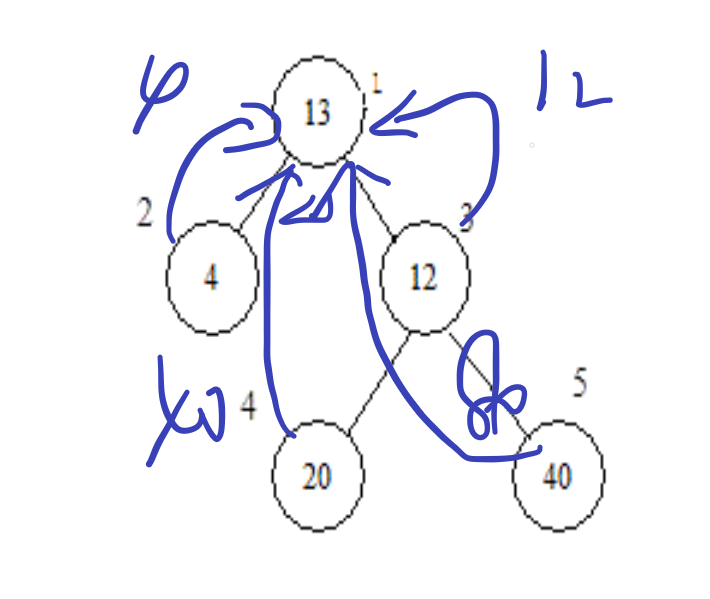
First look at this figure, which shows that if the hospital is built at node 1, the processing is the algorithm of \ (O(n) \).
Then, I changed the hospital now,
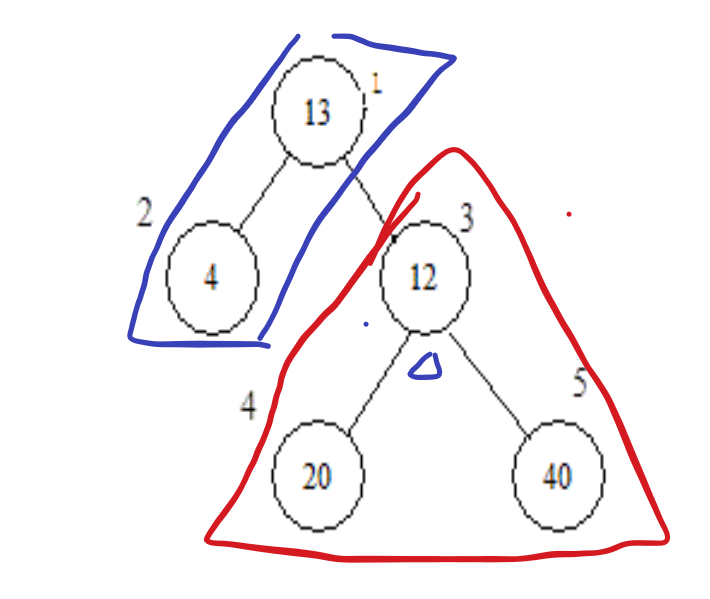
As shown in this figure, the hospital has been changed. You can see that the nodes in the blue area have gone one step less, while other nodes have gone one step more.
This is called root replacement. Please give the ultimate formula for root replacement:
ok, here's the die Code:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
int n;
struct Node{
int p,lc,rc;
}a[114514];
int f[114514],s[114514];
void dfs(int u,int s){
f[1]+=s*a[u].p;
if(a[u].lc) dfs(a[u].lc,s+1);
if(a[u].rc) dfs(a[u].rc,s+1);
return;
}
void dfss(int u,int fa){
s[u]=a[u].p;
if(a[u].lc){
dfss(a[u].lc,u);
s[u]+=s[a[u].lc];
}
if(a[u].rc){
dfss(a[u].rc,u);
s[u]+=s[a[u].rc];
}
return;
}
void ddfs(int u,int fa){
if(a[u].lc){
f[a[u].lc]=f[u]-2*s[a[u].lc]+s[1];
ddfs(a[u].lc,u);
}
if(a[u].rc){
f[a[u].rc]=f[u]-2*s[a[u].rc]+s[1];
ddfs(a[u].rc,u);
}
}
int main(){
cin>>n;
for(int i=1;i<=n;++i) read(a[i].p,a[i].lc,a[i].rc);
dfs(1,0);
dfss(1,-1);
ddfs(1,-1);
int ans=0x3f3f3f3f;
for(int i=1;i<=n;++i)
ans=min(ans,f[i]);
cout<<ans<<endl;
return 0;
}
"NOIP2018 improvement group" track construction
Title Description
City C will host a series of racing competitions. Before the competition, it is necessary to build \ (m \) tracks in the city.
There are \ (n \) intersections in City C, with the numbers of \ (1,2,..., n \) and \ (n − 1 \) two-way roads suitable for the construction of the track, and each road connects two intersections. Among them, the two intersections connected by the \ (I \) road are numbered \ (a_i \) and \ (b_i \), and the length of the road is \ (l_i \). With the help of this \ (n − 1 \) This road can reach all other intersections from any intersection.
A track is a group of roads \ (e_1,e_2,..., e_k \) that are different from each other. You can start from a certain intersection and pass through roads \ (e_1,e_2,..., e_k \) (each road passes once, and turning around is not allowed) to another intersection. The length of a track is equal to the sum of the lengths of all roads. To ensure safety, each road is required to be passed by at most one track.
At present, the scheme of track construction has not been determined. Your task is to design a scheme for track construction, so that the length of the track with the smallest length among the \ (m \) tracks is the largest (that is, the length of the shortest track among the \ (m \) tracks is as large as possible)
Input format
The first line contains two positive integers \ (n,m \) separated by spaces, representing the number of intersections and the number of tracks to be built respectively.
Next line \ (n − 1 \), line I contains three positive integers \ (a_i,b_i,l_i \), representing the two intersection numbers and road length of the road connection suitable for the construction of the track in line \ (I \). Ensure that any two intersections can reach each other through this \ (n − 1 \) road. Two adjacent numbers in each row are separated by a space.
Output format
The output consists of one line, including an integer, indicating the maximum length of the track with the smallest length.
Data range and tips
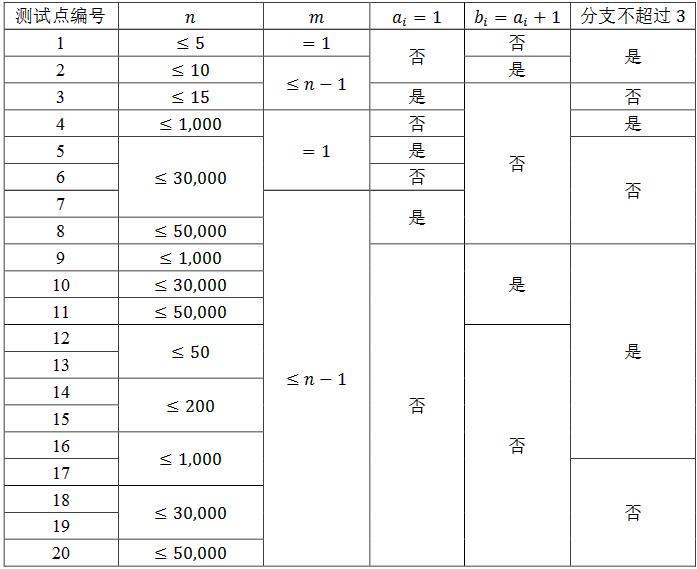
Among them, "branch no more than 3" means that there are at most 3 roads connected to each intersection.
For all data, \ (2 ≤ n ≤ 50000, 1 ≤ m ≤ n − 1, 1 ≤ ai,bi ≤ n, 1 ≤ li ≤ 10000. \)
sample input
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7
sample output
31
thinking
To tell you the truth, this question is very suitable for me. It is a good question of two points + dp on the tree.
If this question can be the last one in 2021 csp-s, I'll take off directly
Not much to say, first of all, I see that the required answer is actually the maximum value of the minimum track length, which is a direct two-point answer. Turn the answer into a critical question.
Both my left and right are closed intervals. I think it is easier to understand that both left and right can succeed.
Let's first look at the weakening data with only three branches, which is the positive solution.
For the three branches, I can only have father nodes and two son nodes. For each path, the contribution to the answer is 1 at most. Then I just need to check whether the sum of the longest chains of the two nodes is greater than the answer I want to judge now.
The problem is still very water.
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar();
while(!('0'<=ch&&ch<='9')){if(ch=='-') t=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=((t<<1)+(t<<3))+ch-'0'; ch=getchar();}
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){
read(t);read(args...);
}
template <typename T>inline void write(T x){
if(x<0) putchar('-'),x=~(x-1); int s[40],top=0;
while(x) s[++top]=x%10,x/=10; if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
}
int n,m;
struct Edge{
int to,nxt,w;
}e[114514];
vector<pair<int,int> >a[114514];
int s,cnt,pos;
int h[114514];
int f[114514];
void add(int u,int v,int w){
e[++pos].to=v;
e[pos].w=w;
e[pos].nxt=h[u];
h[u]=pos;
}
void dfs(int u,int fa,int pos){
multiset<int>se;
for(int i=h[u];i;i=e[i].nxt){
int v=e[i].to,w=e[i].w;
if(v==fa) continue;
dfs(v,u,pos);
if(f[v]+w>=pos){
cnt++;
continue;
}
se.insert(f[v]+w);
}
while(!se.empty()){
multiset<int>::iterator q=se.begin();
se.erase(q);
multiset<int>::iterator p=se.lower_bound(pos-*q);
if(p!=se.end()){
cnt++;
se.erase(p);
}else f[u]=max(f[u],*q);
}
}
bool check(int x){
memset(f,0,sizeof(f));
cnt=0;
dfs(1,-1,x);
if(cnt>=m) return 1;
else return 0;
}
int main(){
cin>>n>>m;
for(int i=1;i<n;++i){
int x,y,w;
read(x,y,w);
s+=w;
add(x,y,w);
add(y,x,w);
}
int left=1,right=s/m+1;
//Both left and right are OK
while(left<right){
int mid=(left+right+1)>>1;
if(check(mid)) left=mid;
else right=mid-1;
}
cout<<left<<endl;
return 0;
}
//19+12 31
There's no need to pick up the watch here, but I'm afraid I'm still running out of water.
Finish scattering flowers!