After brushing the binary tree, we then worked hard on the way of binary search tree~
Binary search tree properties
Search in binary search tree
Iterative method
TreeNode* searchBST(TreeNode* root, int val) {
if(!root) return NULL;
while(root != NULL){
if(val > root->val) root = root->right;
else if(val < root->val) root = root->left;
else break;
}
return root ? root : NULL;
}
Recursive method
TreeNode* searchBST(TreeNode* root, int val) {
if(!root || root->val == val) return root;
if(val > root->val) return searchBST(root->right, val);//If the function has a return value, you must return here
if(val < root->val) return searchBST(root->left, val);
return NULL;
}
There's nothing to say, just pay attention= For null judgment, root - > Val can be used only if it is not empty
Validate binary search tree
I fell into a trap: I thought that as long as the left node of the current node is < the current value, the right node of the current node is > the current value, but it is required that all values on the left subtree of the current node are < the current value, and all values on the right subtree of the current node are > the current value. I want to find the maximum value of the left subtree and the minimum value of the right subtree. But there is a more ingenious method - just traverse the array in middle order and judge whether the array is orderly. (I didn't expect it was really confused)
Recursive method
vector<int> res;
void solve(TreeNode* root){
if(root->left) solve(root->left);
res.push_back(root->val);
if(root->right) solve(root->right);
}
bool isValidBST(TreeNode* root) {
solve(root);
int s = res.size();
for(int i = 0; i < s - 1; i++){
if(res[i+1] <= res[i]) return false;
}
return true;
}
Or you don't have to open the array and judge it directly in the middle order (record the previous one and compare it with the current value)
return when root - > left cannot be judged. Because a tree is a search binary tree, its left and right subtrees are search binary trees.
TreeNode* pre = NULL;
bool isValidBST(TreeNode* root) {
if(!root) return true;
bool left = isValidBST(root->left);
if(pre && pre->val >= root->val) return false;
pre = root;
bool right = isValidBST(root->right);
return left && right;
}
Iterative method
Using stack to simulate middle order traversal? I forgot it all (because I didn't understand it thoroughly at that time)
Note: it is not necessary to push the root node into the stack to simulate the middle order traversal (because the middle order does not start from the following node)
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
while(!st.empty() || cur){
if(cur){
st.push(cur);
cur = cur->left;
}else{
cur = st.top();
st.pop();
if(pre && pre->val >= cur->val) return false;
pre = cur;
cur = cur->right;
}
}
return true;
}
Minimum absolute difference of binary search tree
Recursive method
vector<int> v;
int res = INT_MAX;
void solve(TreeNode* root){
if(root->left) solve(root->left);
v.push_back(root->val);
if(root->right) solve(root->right);
}
int getMinimumDifference(TreeNode* root) {
solve(root);
int s = v.size();
for(int i = 0; i < s-1; i++) res = min(res, v[i+1] - v[i]);
return res;
}
Or you don't have to open the array and record the value of the previous node in the middle order.
Note: this pre pointer must be defined globally
int res = INT_MAX;
TreeNode* pre = NULL;
void solve(TreeNode* cur){
if(cur->left) solve(cur->left);
if(pre) res = min(res, cur->val - pre->val);
pre = cur;
if(cur->right) solve(cur->right);
}
int getMinimumDifference(TreeNode* root) {
solve(root);
return res;
}
Iterative method
Continue to review using the stack to simulate the middle order
Note that the root node is not stacked at the beginning
int getMinimumDifference(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
int res = INT_MAX;
while(!st.empty() || cur){
if(cur){
st.push(cur);
cur = cur->left;
}else{
cur = st.top(); st.pop();
if(pre) res = min(res, cur->val - pre->val);
pre = cur;
cur = cur->right;
}
}
return res;
}
summary
The binary search tree for the maximum value and difference value should take into account that the binary tree is orderly and make good use of this feature.
Mode in binary search tree
Recursive method
map<int, int> count;
int max_count;
void solve(TreeNode* root){
if(root->left) solve(root->left);
count[root->val]++;
max_count = max(max_count, count[root->val]);
if(root->right) solve(root->right);
}
vector<int> findMode(TreeNode* root) {
solve(root);
vector<int> v;
map<int,int>::iterator iter;
for(iter = count.begin(); iter != count.end(); iter++){
if(iter->second == max_count) v.push_back(iter->first);
}
return v;
}
Or just traverse once, or the old routine. Record the previous nodes. Because the middle order traversal binary search tree is orderly, if it is the mode, it must be concentrated in the adjacent area.
vector<int> res;
int max_count, count;
TreeNode* pre = NULL;
void solve(TreeNode* cur){
if(cur->left) solve(cur->left);
if(!pre) count = 1; //First node
else if(pre->val == cur->val) count++;
else count = 1;
pre = cur;
if(count == max_count) res.push_back(cur->val);
if(count > max_count){
max_count = count;
res.clear();
res.push_back(cur->val);
}
if(cur->right) solve(cur->right);
}
vector<int> findMode(TreeNode* root) {
solve(root);
return res;
}
Iterative method
vector<int> res;
int max_count, count;
vector<int> findMode(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
while(!st.empty() || cur){
if(cur){
st.push(cur);
cur = cur->left;
}else{
cur = st.top(); st.pop();
if(pre == NULL) count = 1;
else if(pre->val == cur->val) count++;
else count = 1;
pre = cur;
if(count == max_count) res.push_back(cur->val);
if(count > max_count){
max_count = count;
res.clear();
res.push_back(cur->val);
}
cur = cur->right;
}
}
return res;
}
Nearest common ancestor of binary tree
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == p || root == q || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(left && right) return root;
else if(left) return left;
else if(right) return right;
else return NULL;
}

The solution to this problem is wonderful! I have nothing but praise!
What are you doing there? I'm sweating a lot because I traverse the middle order and take the middle elements. Sure enough, the sword is at the wrong edge again (lll ¬ ω ¬)
Nearest common ancestor of binary search tree
Recursive method
Traverse the search binary tree from bottom to top. Once the value of cur is found between p and q, the nearest common ancestor is found.
Because the search binary tree has the characteristics of medium order, the value between the two must be its father.
TreeNode* res;
void solve(TreeNode* root, TreeNode* p, TreeNode* q){
if(!root) return;
if(root->val >= min(p->val, q->val) && root->val <= max(p->val, q->val)){
res = root;
return;
}
lowestCommonAncestor(root->left, p, q);
lowestCommonAncestor(root->right, p, q);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
solve(root, p, q);
return res;
}
It's different from the standard procedure. I think it's in line with the logic of the preamble, and I don't think I need to return a value (I don't need to traverse the whole tree)
Let's look at the iterative solution (reuse properties)
Iterative method
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while(root){
if(root->val > p->val && root->val > q->val) root = root->left;
else if(root->val < p->val && root->val < q->val) root = root->right;
else return root;
}
return NULL;
}
Modification and construction of binary search tree
Insertion of binary tree search tree
Personally, I think it's quite simple (the data it gives is not strong, and there are many methods. I'm the simplest to insert it directly into the leaves)
Iterative method
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root) return new TreeNode(val);
TreeNode* cur = root;
TreeNode* pre = NULL;
while(cur){
pre = cur;
if(val > cur->val) cur = cur->right;
else cur = cur->left;
}
TreeNode* newNode = new TreeNode(val);
newNode->left = NULL, newNode->right = NULL;
if(val < pre->val) pre->left = newNode;
else pre->right = newNode;
return root;
}
Recursive method
void solve(TreeNode* cur, int val){
if(!cur) return;
if(!cur->left && cur->val > val){
TreeNode* newNode = new TreeNode(val);
cur->left = newNode;
}
if(!cur->right && cur->val < val){
TreeNode* newNode = new TreeNode(val);
cur->right = newNode;
}
if(val > cur->val) solve(cur->right, val);
else solve(cur->left, val);
}
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root) return new TreeNode(val);
solve(root, val);
return root;
}
Delete node of binary search tree
Ah, it's hard to delete!
But be sure to master!
Termination condition: if the node to be deleted is not found, return to root directly
Single layer recursive logic:
① The left and right children are empty (the target node is a leaf node), which can be deleted directly
② The left child is empty and the right child is filled
③ The right child is empty and the left child is filled
④ The left and right children are not empty. Place the left child of the node to be deleted at the left child of the leftmost leaf of the right child, and then the right child fills the space
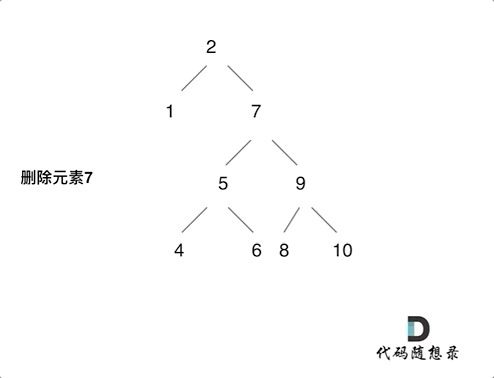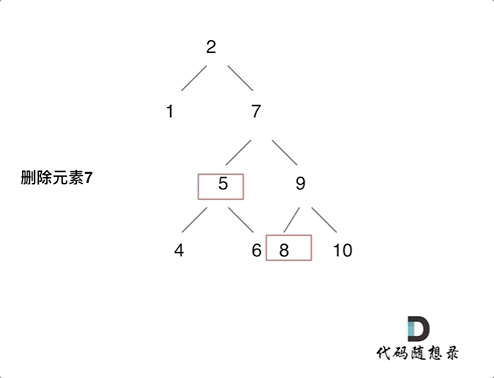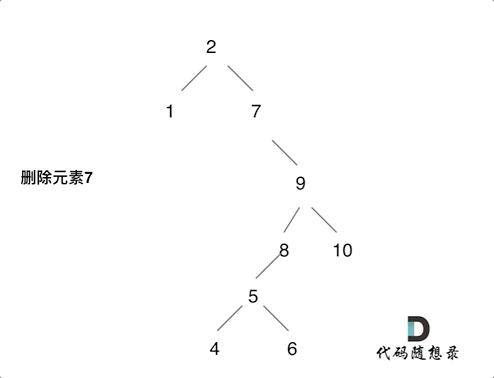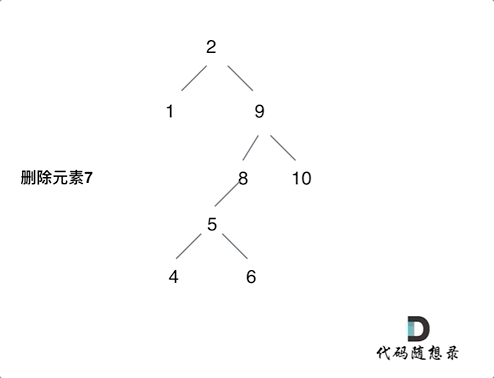
If you find yourself in the devil, stop the loss in time and think about the logic
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root) return root;
if(root->val == key){
if(!root->left && !root->right) return NULL;
else if(!root->left) return root->right;
else if(!root->right) return root->left;
else{
TreeNode* cur = root->right;
while(cur->left) cur = cur->left;
cur->left = root->left;
TreeNode* tmp = root;
root = root->right;
delete tmp;
return root;
}
}
if(root->val < key) root->right = deleteNode(root->right, key);
if(root->val > key) root->left = deleteNode(root->left, key);
return root;
}
The most difficult problem here is to deal with the problems of both left and right children (remember to delete the original root node)
In addition, if you modify, just return. Recursion will eventually return to the root. Note that the left and right children of the root are still used to catch the unmodified places, otherwise the return value is incomplete.
Pruning binary search tree
It's not very difficult (Mastering logic)
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(!root) return NULL;
if(root->val < low){//If its values are smaller than low, its left child is smaller
if(root->right){//Youzi still has some hope
root = root->right;
return trimBST(root, low, high);
}else return NULL;
}
if(root->val > high){//If its values are smaller than high, its right child is larger
if(root->left){//Zuo Zi still has some hope
root = root->left;
return trimBST(root, low, high);
}else return NULL;
}else{
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
}
return root;
}
Construct a binary search tree
TreeNode* solve(vector<int> nums, int begin, int end){
if(begin > end) return NULL;
int mid = (begin + end) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = solve(nums, begin, mid-1);
root->right = solve(nums, mid+1, end);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
int s = nums.size();
if(s == 0) return NULL;
else return solve(nums, 0, s-1);
}
Using the order of binary search tree, we can find that it is twice as simple as the previous construction of binary tree!
Convert binary search tree into cumulative tree
I know the order is right, middle and left, but I can't think of it because I'm hungry~
You need to use pre to record the value of the previous node. I know this. If you are full and energetic, it will be solved easily (if you know the traversal order, there will be no problem to embarrass me)
int pre;
void solve(TreeNode* cur){
if(!cur) return;
solve(cur->right);
cur->val += pre;
pre = cur->val;
solve(cur->left);
}
TreeNode* convertBST(TreeNode* root) {
pre = 0;
solve(root);
return root;
}
awesome! It's true that I can eat very much recently@_@
