Linked list
Single linked list
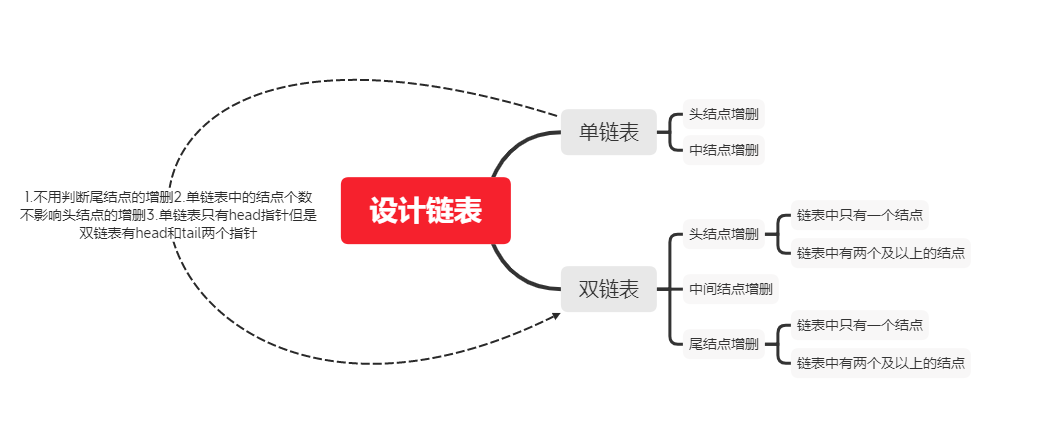
Design single linked list
Note: it is not difficult to delete nodes in the middle and insert nodes in the middle, but header insertion or deletion should be considered when inserting or deleting nodes arbitrarily. It should be noted that if the head node changes, the head node will change. Therefore, when inserting or deleting a node, you need to pay special attention to the insertion and deletion of the head node.
class MyLinkedList {
private:
struct ListNode
{
int val;
ListNode* next;
ListNode(int v = 0) :val(v), next(nullptr) {}
};
int size;// Length of linked list
ListNode* head;// Head pointer
public:
/** Initialize your data structure here. */
MyLinkedList() :size(0), head(nullptr) {
}
/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
int get(int index) {
if (index + 1 > size)
return -1;
ListNode* cur = head;
while (index--)
{
cur = cur->next;
}
return cur->val;
}
/** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
void addAtHead(int val) {
addAtIndex(0, val);
}
/** Append a node of value val to the last element of the linked list. */
void addAtTail(int val) {
addAtIndex(size, val);
}
/** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */
void addAtIndex(int index, int val) {
ListNode* newNode = new ListNode(val);
// Head insert
if (index <= 0)
{
newNode->next = head;// newNode points to head, and then newNode becomes head
head = newNode;
size++;
return;
}
// The index is greater than the length of the linked list
if (index > size)
return;
// Intermediate insertion node
ListNode* prev = head;
while (--index)// Find the previous node of index
{
prev = prev->next;
}
newNode->next = prev->next;
prev->next = newNode;
size++;// Linked list length + 1
}
/** Delete the index-th node in the linked list, if the index is valid. */
void deleteAtIndex(int index) {
if (index < 0 || index >= size)// No index < 0 or > = size
return;
if (index == 0)// Delete header node
{
ListNode* delNode = head;
head = head->next;
delete delNode;
}
else// Delete intermediate node
{
ListNode* prev = head;
while (-- index)// Find the previous node of index
{
prev = prev->next;
}
ListNode* delNode = prev->next;
prev->next = delNode->next;
delete delNode;
}
size --;// Linked list length - 1
}
};
Double pointer in linked list
Circular linked list
(speed pointer)
Note that both fast and slow pointers need to be initialized to head when initializing, so you can use fast= Slow as a condition of the while loop
class Solution {
public:
bool hasCycle(ListNode *head) {
if (head == nullptr || head->next == nullptr) return false;
ListNode* fast = head, *slow = head;
// Method 1
while (fast && fast->next)
{
fast = fast->next->next;// fast takes two steps at a time
slow = slow->next;// The slow pointer takes one step at a time
if (fast == slow)
return true;
}
return false;
// Method 2
// while (fast != nullptr)
// {
// fast = fast->next;
// if (fast != nullptr)
// fast = fast->next;
// slow = slow->next;
// if (fast == slow)
// return true;
// }
// return false;
}
};
Circular linked list II
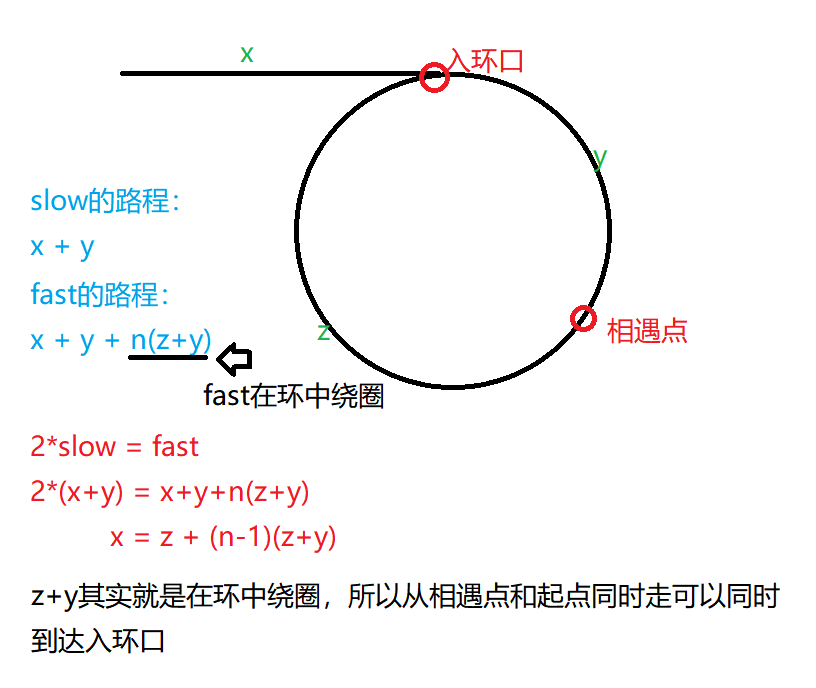
(speed pointer)
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
// Judge whether there is a ring
ListNode* fast = head, *slow = head;
ListNode* meetNode = nullptr;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if (fast == slow)
{
meetNode = fast;
break;
}
}
// If there is no ring in the linked list, nullptr is returned
if (meetNode == nullptr)
return nullptr;
// Let head and meetNode go at the same time to know that they will meet at the entrance
while (head != meetNode)
{
head = head->next;
meetNode = meetNode->next;
}
return meetNode;
}
};
Intersecting linked list
(pointer interleaving traversal 1)
Because the number of nodes after the intersection point is the same, but the number of nodes before the intersection point is different. If the two pointers have the same number of nodes, they can reach the intersection point at the same time. Therefore, let the curA pointer go through the curA linked list and then go through the curB linked list. Let the curB pointer go through the curB linked list and then go through the curA linked list. In this way, it can make up for the possible difference in the number of nodes before the intersection point, resulting in the difference in the number of nodes.
Summary: I can't see you at the end, so I walk the way you came. When I meet, I find that you also walk the way I came
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA, *curB = headB;
while (curA != curB)
{
curA = curA->next;
curB = curB->next;
// If you go to nullptr at the same time, it means that the linked list has no intersection
if (curA == nullptr && curB == nullptr) return nullptr;
// If the linked list goes through one linked list, go to another linked list
if (curA == nullptr) curA = headB;
if (curB == nullptr) curB = headA;
}
return curA;
}
};
(pointer interleaving traversal 2)
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* curA = headA, *curB = headB;
while (curA != curB)
{
curA = curA ? curA->next : headB;
curB = curB ? curB->next : headA;
}
return curA;
}
};
(linked list to find the ring port)
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
// Find the tail of list A
ListNode* cur = headA;
while (cur->next != nullptr)
cur = cur->next;
// Connect linked list A to linked list B
cur->next = headB;
// Find the ring mouth
ListNode* fast = headA, *slow = headA;
while (fast && fast->next)
{
fast = fast->next->next;
slow = slow->next;
if (slow == fast)
{
ListNode* prev = headA;
while (prev != slow)
{
prev = prev->next;
slow = slow->next;
}
// Restore linked list
cur->next = nullptr;
return prev;
}
}
// Restore linked list
cur->next = nullptr;
return nullptr;
}
};
(make up the difference in the linked list)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int cntA = 0, cntB = 0;
ListNode* curA = headA, *curB = headB;
// Count the length of the linked list
while (curA)
{
curA = curA->next;
cntA ++;
}
while (curB)
{
curB = curB->next;
cntB ++;
}
// greater is a long linked list and less is a short linked list
ListNode* greater = cntA > cntB ? headA : headB;
ListNode* less = greater == headA ? headB : headA;
// Let the long linked list take the difference steps first and make up the difference
int n = abs(cntA - cntB);
for (int i = 0; i < n; i ++)
greater = greater->next;
// Long list and short list go together until they meet
while (greater != less)
{
greater = greater->next;
less = less->next;
}
return greater;
}
};
Delete the penultimate node of the linked list
(speed pointer)
Three tips:
1) To find the penultimate node, the fast pointer can go n steps first, so that the slow pointer can go from the beginning of the node to fast at the same time. In this way, when fast comes to the end, the slow pointer will go to the penultimate node. The step difference and relative position are usually used to simplify the algorithm in the two tables.
2) Set the virtual head Street point, so you can delete the head node like deleting the intermediate node
3) The slow pointer needs to go to the last position of the deleted node. Starting from dummy, you can go to the penultimate node n+1. If you start from head, you can only go to the penultimate node n
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* fast = head;
// Let the fast pointer go n steps first
while (n --)
fast = fast->next;
// Take fast as the end of the linked list and go with the slow pointer
// When the fast pointer reaches the end of the linked list, the slow pointer reaches the penultimate position
// Because the head node may be deleted, set a virtual head node
ListNode* dummy = new ListNode(-1);
dummy->next = head;
// Let slow start from dummy, and you can just take one step less, so that you can go to the last position of the deleted node
ListNode* slow = dummy;
while (fast != nullptr)
{
fast = fast->next;
slow = slow->next;
}
// Because there is a virtual head node, you can delete a node without considering the head node
ListNode* delNode = slow->next;
slow->next = delNode->next;
delete delNode;
ListNode* newHead = dummy->next;
delete dummy;
return newHead;
}
};
Classical problem
Reverse linked list
Title Requirements: reverse a linked list
(head insertion method)
class Solution {
public:
ListNode* reverseList(ListNode* head) {
// New head node of linked list
ListNode* newHead = nullptr;
// Use cur to traverse the original linked list to get the head knot
ListNode* cur = head;
while (cur != nullptr)
{
// Keep the next node
ListNode* next = cur->next;
// Head insertion node
cur->next = newHead;
// Update new header node
newHead = cur;
// Traverse the next linked list node
cur = next;
}
return newHead;
}
};
(recursive)
It should be noted that newHead remains unchanged during recursive return. After finding the head of the inverted linked list, it will always return its head node.
Generally, head == nullptr will not be triggered, because when traversing the linked list, head - > next = = nullptr will stop. However, if the linked list is empty, you need to use head == nullptr for special judgment.
In fact, when writing this recursion, it is divided into two parts
1) The first is to reverse the original linked list except the head node, and then return to the head node of the inverted linked list
2) The second is to deal with the head node, but it should be clear that the head node at this time is not only the head node, but all nodes at the time of recursion, and the processing method of these nodes is the same as that of the current head node. Therefore, as long as the next node of the head node points to the head node, the reverse effect has been achieved. However, just said that because the processing of the head node is the processing of all nodes, the head node itself should be pointed to nullptr. Although the pointing of the intermediate node to nullptr is meaningless, in this way, the end of the whole linked list can point to nullptr, Otherwise, the end node of the linked list will not point to nullptr and the cycle of the linked list will be dead
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (head == nullptr || head->next == nullptr)
return head;
// Reverse the linked list except the head node, and return the head node of the following linked list
ListNode* newHead = reverseList(head->next);
// Processing header node
head->next->next = head;
head->next = nullptr;
// Returns the head node of the new linked list
return newHead;
}
};
Remove linked list elements
Topic requirements: remove the node with the value equal to val in the linked list
(set virtual head node 1)
Because the removed node is the head node, it is more convenient to set the virtual head node. In this way, the steps of deleting the head node are the same as those of deleting the intermediate node.
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
// Set virtual head node
ListNode* dummy = new ListNode(-1);
dummy->next = head;
ListNode* cur = dummy;
// Because each cycle will go down once, so use cur= Nullptr ensure cur exists
// At the same time, ensure that cur has the next node
while (cur != nullptr && cur->next != nullptr)
{
// If there is a next node and the value of the next node is equal to val, the next node of the node will be deleted
// Note that this is a while circular deletion, because the values of several consecutive nodes below may be equal to val
// If you use if, after jumping out of the loop, cur = cur - > next, so you can't delete the cur node
while (cur->next != nullptr && cur->next->val == val){
ListNode* delNode = cur->next;
cur->next = delNode->next;
delete delNode;
}
cur = cur->next;
}
ListNode* newHead = dummy->next;
delete dummy;
return newHead;
}
};
(* set virtual head node 2 + double pointer)
This method is easier to understand. Use two pointers prev and cur. Cur is used to judge whether cur - > val is equal to val in the front. If it is prev, you can skip the cur node and directly point to the next node of cur. Then cur goes down one step until the value of cur is not equal to val, let prev = cur, and then cycle like this. Stop when cur is empty. But it should be noted that because the node cur may be deleted in the middle, in order to make the linked list cycle later, it is required to save the next node of cur when entering the cycle to ensure that the linked list can cycle.
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummy = new ListNode(-1);
dummy->next = head;
ListNode* prev = dummy, *cur = head;
while (cur != nullptr)
{
ListNode* next = cur->next;
// If the value of cur is val, delete cur, otherwise let prev=cur enter the next deletion process
if (cur->val == val)
{
prev->next = cur->next;
delete cur;
}
else
prev = cur;
cur = next;
}
prev = dummy->next;
delete dummy;
return prev;
}
};
(set virtual head node 3 + single pointer)
For the deletion node implemented with double pointers above, one pointer is less used here. In fact, it is the same logic
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummy = new ListNode(-1);
dummy->next = head;
ListNode* cur = dummy;
// No cur= Nullptr because cur = cur - > next only when cur - > next exists, cur must exist
while (cur->next != nullptr)
{
if (cur->next->val == val)
{
ListNode* delNode = cur->next;
cur->next = cur->next->next;
delete delNode;
}
else
cur = cur->next;
}
cur = dummy->next;
delete dummy;
return cur;
}
};
(recursive)
class Solution {
public:
// Returns the head node of the linked list after deleting the val node
ListNode* removeElements(ListNode* head, int val) {
if (head == nullptr)
return head;
// The linked list behind head has deleted the node with value equal to val
head->next = removeElements(head->next, val);
// Handle the header node. If head - > Val = = Val, head - > next will be returned; otherwise, head will be returned
if (head->val == val)
{
ListNode* next = head->next;
delete head;
return next;
}
else
return head;
}
};
Parity linked list
Topic requirements: put the node on the odd bit in front of the node on the even bit
(create two linked lists + three pointers by tail interpolation)
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
// If the number of nodes is < = 2, it will directly return to the linked list itself
if (!head || !head->next || !head->next->next)
return head;
ListNode* cur = head->next->next;
// Create odd even linked list
ListNode* odd = head, *even = head->next;
ListNode* evenHead = even;
// Determine which linked list should be inserted into at present
bool flag = true;
while (cur != nullptr)
{
// tmp is used to indicate which linked list should be inserted into at present
ListNode* tmp = nullptr;
if (flag)
tmp = odd;
else
tmp = even;
// Keep the backup of the next node of cur
ListNode* next = cur->next;
// Connect cur to the back of the linked list
cur->next = nullptr;
tmp->next = cur;
// Let the head node of the linked list move back one bit
if (flag)
odd = odd->next;
else
even = even->next;
// cur traverses the nodes in the original linked list
cur = next;
// Parity exchange
flag = !flag;
}
// Let the even linked list on the street behind the odd linked list
odd->next = evenHead;
// Let even linked list point to empty
even->next = nullptr;
return head;
}
};
(create parity linked list + double pointer)
This method is easier to understand
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
ListNode* evenHead = new ListNode(-1);
ListNode* oddHead = new ListNode(-1);
ListNode* even = evenHead, *odd = oddHead;
int count = 1;// Judging parity linked list with count
while (head != nullptr)
{
if ((count & 1) == 1)
{
odd->next = head;
odd = odd->next;
}
else
{
even->next = head;
even = even->next;
}
count ++;
head = head->next;
}
// The odd linked list is followed by the even linked list, and the tail of the even linked list points to nullptr
odd->next = evenHead->next;
even->next = nullptr;
// Delete nodes to prevent memory leakage
ListNode* newHead = oddHead->next;
ListNode* del = oddHead;
delete del;
del = evenHead;
delete del;
return newHead;
}
};
Using the double pointer method to solve the problem of splitting the linked list, this problem is to separate the nodes of odd digits from the nodes of even digits. Using this method, we can also solve the problems such as: the node with value < = Val is placed in front of the node with value > val
(* parity interleaving + single pointer)
It is more ingenious to apply to this problem
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
if (head == nullptr) return head;
ListNode* odd = head, *even = head->next;
ListNode* evenHead = even;
while (even != nullptr && even->next != nullptr)
{
// The odd number points to the next even number and then moves back one bit
odd->next = even->next;
odd = odd->next;
// The even number points to the next odd number and then moves back one bit
even->next = odd->next;
even = even->next;
}
// Odd linked list connected to even linked list
odd->next = evenHead;
return head;
}
};
Palindrome linked list
Title Requirements: judge whether the linked list is a palindrome linked list
(find intermediate node + reverse linked list)
Find the middle node first, and then divide the whole linked list into two linked lists, reverse the latter half of the linked list, and finally compare the two linked lists. If the values of all nodes are the same, it is a palindrome linked list, otherwise it is not a palindrome linked list. (if the number of nodes in the linked list is odd, it doesn't matter. When comparing the linked list, just compare the number of short linked lists several times)
class Solution {
public:
bool isPalindrome(ListNode* head) {
if (head == nullptr || head->next == nullptr) return true;
ListNode* fast = head, *slow = head;
while (fast != nullptr && fast->next != nullptr)
{
fast = fast->next->next;
slow = slow->next;
}
// Reverse the linked list of the second half
ListNode* cur = slow, *newHead = nullptr;
while (cur != nullptr)
{
ListNode* next = cur->next;
cur->next = newHead;
newHead = cur;
cur = next;
}
// Compare the two linked lists
while (newHead && head)
{
if (newHead->val != head->val)
return false;
newHead = newHead->next;
head = head->next;
}
return true;
}
};
Find the intermediate node O(N) + reverse the linked list O(N) + compare the two linked lists O(N), so the time complexity is O(N)
(save the value of the linked list with an array)
class Solution {
public:
bool isPalindrome(ListNode* head) {
vector<int> ans;
ListNode* cur = head;
// Put the values of nodes in the linked list into the array
while (cur != nullptr)
{
ans.push_back(cur->val);
cur = cur->next;
}
// Compare whether the values in the array are palindromes with double pointers
int i = 0, j = ans.size() - 1;
while (i < j)
{
if (ans[i++] != ans[j--])
return false;
}
return true;
}
};
Double linked list
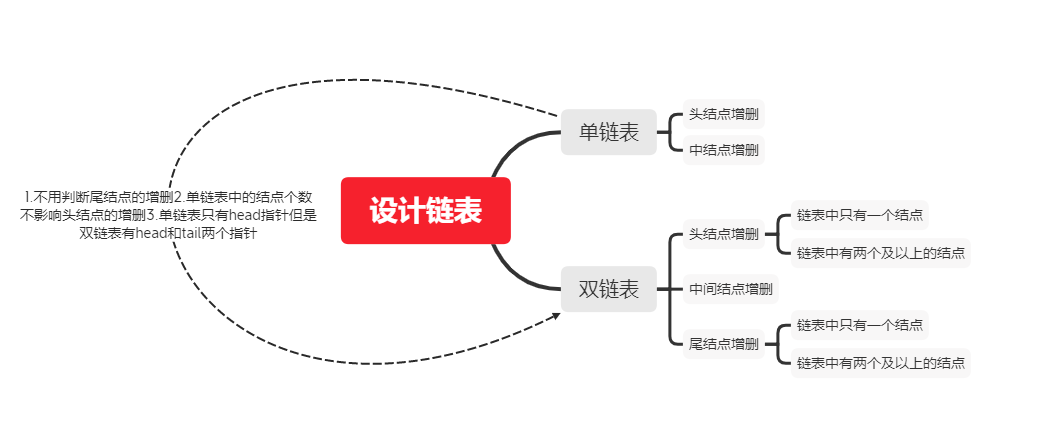
When designing a double linked list, what is more troublesome than a single linked list is that not only the head node but also the tail node of the double linked list need special judgment. Because the movement of the head node of the single linked list is related to the movement of the head, the addition and deletion of the head node need special judgment, but the tail node has no impact, However, not only the head node of the double linked list will affect the movement of the head, but also because the double linked list has two pointers, one prev and one next. Therefore, if the tail node is deleted, the nullptr behind the tail node cannot point to other nodes, otherwise the error of nullptr dereference will be reported at this time.
Design linked list
(1 only one head)
class MyLinkedList {
private:
struct ListNode
{
int val;
ListNode* prev, *next;
ListNode(int v):val(v), prev(nullptr), next(nullptr) {}
};
int size;
ListNode* head;
public:
/** Initialize your data structure here. */
MyLinkedList() {
size = 0;
head = nullptr;
}
/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
int get(int index) {
if (index + 1 > size)
return -1;
ListNode* cur = head;
while (index --)
{
cur = cur->next;
}
return cur->val;
}
/** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
void addAtHead(int val) {
addAtIndex(0, val);
}
/** Append a node of value val to the last element of the linked list. */
void addAtTail(int val) {
addAtIndex(size, val);
}
/** Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. */
void addAtIndex(int index, int val) {
// index is greater than the length of the linked list
if (index > size)
return ;
ListNode* newNode = new ListNode(val);
// Insert node in the first position
if (index <= 0)
{
newNode->next = head;
newNode->prev = nullptr;
// If the linked list is not empty (there are nodes in the linked list instead of empty), let the original head point to the new node
if (head != nullptr)
head->prev = newNode;
head = newNode;
}
else if (index < size)// Insert node in middle position
{
ListNode* cur = head;
while (index --)
cur = cur->next;
newNode->next = cur;
newNode->prev = cur->prev;
cur->prev->next = newNode;
cur->prev = newNode;
}
else if (index == size)// Insert node at end
{
ListNode* cur = head;
while (cur->next != nullptr)
cur = cur->next;
newNode->next = nullptr;
newNode->prev = cur;
cur->next = newNode;
}
size ++;
}
/** Delete the index-th node in the linked list, if the index is valid. */
void deleteAtIndex(int index) {
// If the first preceding node is deleted or exceeds the length of size, void is returned
if (index < 0 || index >= size) return ;
// Delete header node
if (index == 0)
{
// Focus on moving the head to the current newNode position when the head node is deleted
// And there is a special case. If there is only one node in the linked list, then head=nullptr is OK
// Do not use newnode - > prev = nullptr. In this case, nullptr dereference and error will be reported
ListNode* delNode = head;
if (size == 1)
{
head = nullptr;
delete delNode;
}
else
{
delNode->next->prev = nullptr;
head = delNode->next;
delete delNode;
}
}
else if (index < size - 1)// Delete intermediate node
{
ListNode* cur = head;
while (index --)
cur = cur->next;
ListNode* prevNode = cur->prev;
ListNode* nextNode = cur->next;
prevNode->next = nextNode;
nextNode->prev = prevNode;
delete cur;
}
else if (index == size - 1)// Delete tail node
{
ListNode* cur = head;
while (cur->next != nullptr)
cur = cur->next;
cur->prev->next = nullptr;
delete cur;
}
size --;
}
};
Using the above code, we can see that there are many situations to consider when deleting a double linked list, and we should pay special attention to some details
(2 use head+tail)
After setting the virtual head node and tail node, there is no need to specially consider the insertion and deletion of head node and tail node, because the addition and deletion of head node and tail node and intermediate node are the same at this time.
Like the single linked list, when deleting, you need to pay special attention to the details of deleting the head node and tail node. This problem is difficult because it needs to be discussed in many situations:
class MyLinkedList {
private:
struct ListNode
{
int val;
ListNode* prev, * next;
ListNode(int v):val(v), prev(nullptr), next(nullptr) {}
};
ListNode* head, *tail;
int size;
public:
/** Initialize your data structure here. */
MyLinkedList():size(0), head(nullptr), tail(nullptr) {}
/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
int get(int index) {
int i = 0;
ListNode* cur = head;
while (cur && i < index)
{
cur = cur->next;
i ++;
}
if (cur) return cur->val;
else return -1;
}
/** Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. */
void addAtHead(int val) {
ListNode* newNode = new ListNode(val);
if (head != nullptr)
{
newNode->next = head;
head->prev = newNode;
head = newNode;
}
else
{
head = newNode;
tail = head;// The order here cannot be reversed. head must be assigned to tail
}
size ++;
}
/** Append a node of value val to the last element of the linked list. */
void addAtTail(int val) {
ListNode* newNode = new ListNode(val);
if (tail != nullptr)
{
newNode->prev = tail;
tail->next = newNode;
newNode->next = nullptr;
tail = newNode;
}
else
{
tail = newNode;
head = tail;
}
size ++;
}
// Insert node in front of index
void addAtIndex(int index, int val) {
if (index <= 0) addAtHead(val);
else if (index == size) addAtTail(val);
else if (index > size) return;
else
{
ListNode* cur = head;
while (index --)
cur = cur->next;
ListNode* newNode = new ListNode(val);
ListNode* prevNode = cur->prev;
prevNode->next = newNode;
newNode->prev = prevNode;
newNode->next = cur;
cur->prev = newNode;
size ++;
}
}
/** Delete the index-th node in the linked list, if the index is valid. */
void deleteAtIndex(int index) {
if (size == 0) return ;
if (index == 0)// Delete header node
{
ListNode* delNode = head;
head = head->next;
// There is only one node in the linked list
if (head == nullptr)
{
tail = nullptr;
}
else // More than one node in the linked list
{
head->prev = nullptr;
}
delete delNode;
size --;
}
else if (index < size - 1)// Delete intermediate node
{
ListNode* cur = head;
while (index --)
cur = cur->next;
ListNode* delNode = cur;
ListNode* prevNode = cur->prev;
ListNode* nextNode = cur->next;
prevNode->next = nextNode;
nextNode->prev = prevNode;
delete delNode;
size --;
}
else if (index == size - 1)// Delete tail node
{
ListNode* delNode = tail;
tail = tail->prev;
// There is only one node in the linked list
if (tail == nullptr)
{
head = nullptr;
}
else// More than one node in the linked list
{
tail->next = nullptr;
}
delete delNode;
size --;
}
}
};
Linked list summary
If you need to add or delete nodes often, linked list may be a good choice.
If you need to access elements by index often, arrays may be a better choice than linked lists.
Merge two ordered linked lists
(similar to merging ordered arrays)
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if (l1 == nullptr) return l2;
if (l2 == nullptr) return l1;
ListNode* cur1 = l1, *cur2 = l2;
// Set the head node to put back the pointer, and set the tail node to insert the node at the end of the linked list
ListNode* tail = nullptr, *head = nullptr;
// First set the first node of the header pointer
if (cur1->val < cur2->val)
{
head = tail = cur1;
cur1 = cur1->next;
}
else
{
head = tail = cur2;
cur2 = cur2->next;
}
tail->next = nullptr;
// Continue when neither pointer is nulltpr
while (cur1 && cur2)
{
// Let the linked list be followed by a node with a small value
if (cur1->val < cur2->val)
{
ListNode* next = cur1->next;
tail->next = cur1;
cur1->next = nullptr;
tail = cur1;
cur1 = next;
}
else
{
ListNode* next = cur2->next;
tail->next = cur2;
cur2->next = nullptr;
tail = cur2;
cur2 = next;
}
}
if (cur1) tail->next = cur1;
if (cur2) tail->next = cur2;
return head;
}
};
(recursive version)
class Solution {
public:
// Returns the head node of the merged two linked lists
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// If a linked list is empty, it will directly return to another linked list
if (l1 == nullptr) return l2;
if (l2 == nullptr) return l1;
// Compare the size of the value of the chain header
// Let the link list 1 with a small value of the chain header be followed by the result of the combination of the part behind link list 1 and link list 2
if (l1->val < l2->val) {
l1->next = mergeTwoLists(l1->next, l2);
return l1;
} else {
l2->next = mergeTwoLists(l1, l2->next);
return l2;
}
}
};
(virtual head node)
This problem is to merge the new linked list, but the head node has not been determined, so we can think of using virtual head node.
==Generally speaking, the biggest function of the virtual head node is to treat all nodes equally = = because the addition and deletion of the head node will often lead to the change of the head pointer of the linked list, so when the general head node wants to change, it needs to judge the head node specially.
The advantage of using virtual head node in this problem can not only save the trouble of head node insertion, but also do not need to find which head node in the two linked lists has a larger value (treat the head nodes equally).
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// Set virtual head node
ListNode* dummy = new ListNode(-1);
ListNode* cur = dummy;
while (l1 && l2)
{
if (l1->val < l2->val)
{
cur->next = l1;
l1 = l1->next;
}
else
{
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
// Connect the part of the linked list that is not connected
if (l1) cur->next = l1;
else cur->next = l2;
ListNode* head = dummy->next;
delete dummy;
return head;
}
};
Add two numbers
Subject requirements: treat each node of the linked list as a single digit (inverted, which means that the tail node of the linked list is the highest and the head node is the lowest), add the two numbers of the two linked lists, and then turn each digit of the result into a node to form a new linked list (or inverted)
(linked list to array + large number addition + array to linked list)
This problem can't be converted from a linked list to a number, because there are at most 100 nodes, so even long long can't store more than 16 digits. Therefore, if you want to convert the value of the linked list into a number, you can only store the number in the vector, add the large number of vector+vector, and finally convert the number in the array into a linked list.
class Solution {
public:
vector<int> Add(vector<int>& v1, vector<int>& v2){
vector<int> sum;
int carry = 0;// carry
int i = 0;
while (i < v1.size() || i < v2.size())
{
int num1 = 0;
if (i < v1.size())
num1 = v1[i];
int num2 = 0;
if (i < v2.size())
num2 = v2[i];
int t = num1 + num2 + carry;
sum.push_back(t % 10);
// carry
if (t > 9) carry = 1;
else carry = 0;
i ++;
}
if (carry == 1) sum.push_back(1);
reverse(sum.begin(), sum.end());
return sum;
}
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
vector<int> v1, v2;
ListNode* cur1 = l1, * cur2 = l2;
// Linked list to array
while (cur1 != nullptr)
{
v1.push_back(cur1->val);
cur1 = cur1->next;
}
while (cur2 != nullptr)
{
v2.push_back(cur2->val);
cur2 = cur2->next;
}
// Addition of large numbers
vector<int> sum = Add(v1, v2);
// Array to linked list (set virtual head node)
ListNode* dummy = new ListNode(-1);
ListNode* cur = dummy;
while (!sum.empty())
{
ListNode* newNode = new ListNode(sum.back());
sum.pop_back();
cur->next = newNode;
cur = cur->next;
}
cur->next = nullptr;
ListNode* head = dummy->next;
delete dummy;
return head;
}
};
(linked list directly to linked list 1)
You can also add the values of each node of the linked list and merge the linked list at the same time.
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* dummy = new ListNode(-1);
ListNode* cur = dummy;
ListNode* cur1 = l1, * cur2 = l2;
int carry = 0;
// When both linked lists are finished and there is no carry, it ends
while (cur1 || cur2 || carry == 1)
{
// Take out the value of the linked list node
int num1 = cur1 == nullptr ? 0 : cur1->val;
int num2 = cur2 == nullptr ? 0 : cur2->val;
int sum = num1 + num2 + carry;
ListNode* newNode = new ListNode(sum % 10);
cur->next = newNode;
cur = cur->next;
// carry
carry = sum / 10;
// Two linked lists go back at the same time
if (cur1) cur1 = cur1->next;
if (cur2) cur2 = cur2->next;
}
ListNode* head = dummy->next;
delete dummy;
return head;
}
};
(linked list to linked list 2)
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* dummy = new ListNode(-1);
ListNode* cur = dummy;
ListNode* cur1 = l1, * cur2 = l2;
int sum = 0;
// When both linked lists are finished and there is no carry, it ends
while (cur1 || cur2 || sum == 1)
{
if (cur1)
{
sum += cur1->val;
cur1 = cur1->next;
}
if (cur2)
{
sum += cur2->val;
cur2 = cur2->next;
}
cur->next = new ListNode(sum % 10);
cur = cur->next;
// carry
sum /= 10;
}
ListNode* head = dummy->next;
delete dummy;
return head;
}
};
Rotating linked list
Title Requirements: given a linked list and the number k, rotate the linked list to the right K positions
The general idea is: find the penultimate position k+1, then disconnect, let the tail node of the linked list point to the head of the original linked list, and finally sit the penultimate position k as a new head node to form a new linked list.
(the speed pointer finds the penultimate node 1)
Using the fast and slow pointer, let the fast pointer go k steps first, and then let the fast pointer and the slow pointer go at the same time. If the fast pointer goes to nullptr, slow will go to the penultimate node. If fast goes to the last node instead of nullptr, slow will go to the penultimate node. This is the use of the relative position of the fast and slow pointer to solve the problem.
Note: using the double pointer, you can find the penultimate k+1 node in the case of traversal. However, because the value of k is uncertain, if k is greater than the number of linked lists, you can't rotate right, so you must find the total number of nodes in the linked list.
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if (head == nullptr || head->next == nullptr || k == 0) return head;
// Calculate the total number of nodes in the linked list
int cnt = 0;
ListNode* cur = head;
while (cur)
{
cnt ++;
cur = cur->next;
}
// k must be less than the total number of nodes in the linked list
k %= cnt;
// Use two pointers to find the end of the linked list and the penultimate position k+1
ListNode* fast = head, *slow = head;
while (k --)
fast = fast->next;
// Because the penultimate k+1 node is found, fast goes to the last node
// Find the penultimate node fast to nullptr
while (fast->next)
{
slow = slow->next;
fast = fast->next;
}
// Disconnect the linked list and reconnect
if (slow->next == nullptr)
return head;
ListNode* newHead = slow->next;
slow->next = nullptr;
fast->next = head;
return newHead;
}
};
When disconnecting the linked list, pay attention to the order.
There are three tasks in the process of disconnecting and reconnecting the linked list:
1) Find the next node of the penultimate k+1 node as the beginning of the new linked list
2) Point the last k+1 node to nullptr to disconnect the linked list
3) Change the linked list into the original chain header of foreign exchange settlement
The above method is carried out in the order of (1,2,3), but there is a special case to be judged at this time. If there is only one node newHead in the linked list as the chain header directly, there is a problem. Because there is only one node, slow - > next is nullptr, but how can a node rotate without a node? Therefore, it is necessary to make a special judgment. If slow - > next is empty, you can directly return to the header node.
(the speed pointer finds the penultimate node 2)
Change the above method to another order (3, 1, 2), and first make the linked list form a closed loop. In this way, it is even a node, but slow - > next will point to itself.
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if (head == nullptr || head->next == nullptr || k == 0) return head;
// Calculate the total number of nodes in the linked list
int cnt = 0;
ListNode* cur = head;
while (cur)
{
cnt ++;
cur = cur->next;
}
// k must be less than the total number of nodes in the linked list
k %= cnt;
ListNode* fast = head, *slow = head;
while (k --)
fast = fast->next;
while (fast->next)
{
slow = slow->next;
fast = fast->next;
}
// Let the linked list form a closed loop
fast->next = head;
ListNode* newHead = slow->next;
slow->next = nullptr;
return newHead;
}
};
(simple version)
This method is very simple. Counting the total number of nodes and finding the end of the linked list are a separate cycle, but when looking for the end of the linked list, you can find the total number of nodes by the way. As long as you start counting not from 0, but directly from the beginning, so few nodes can be made up.
Another point is that since the total number of nodes has been calculated, you can directly use a pointer to take the total number - k-1 step to the penultimate k+1 position without double pointer traversal. The next time you encounter a problem, you can only traverse once, and then use double pointers when you find the penultimate node.
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if (head == nullptr || head->next == nullptr)
return head;
// Calculate the total number of nodes in the linked list and let cur find the end of the linked list
int cnt = 1;
ListNode* cur = head;
while (cur->next)
{
cnt ++;
cur = cur->next;
}
// k must be less than the total number of nodes in the linked list
k %= cnt;
// Here's a special judgment. If k is a multiple of cnt or k is originally 0
// It indicates that the original linked list does not need to be rotated
if (k == 0) return head;
// Let the linked list form a closed loop
cur->next = head;
// Find the penultimate position k+1
for (int i = 0; i < cnt - k - 1; i ++)
head = head->next;
ListNode* newHead = head->next;
head->next = nullptr;
return newHead;
}
};