SQL07 set calculation

Relational Division

Define table R and table S as follows

R

X	Y
X1	Y1
X2	Y2
X2	Y3
X2	Y3
X3	Y1
X3	Y2

S

Y	F
Y1	F1
Y2	F2

For relationships (tables) with the same attributes, R and S relationship division is mainly divided into the following steps:

1. Find the same attribute y. Project y in relation R, that is, take out the value of Y

​ Y->{Y1, Y2}

2. The attribute column in the divided relation R that is different from that in S is x, and the relation R does the projection (de duplication) X1 and X2 of the de duplicated value on the attribute X

3. Obtain the image set corresponding to X attribute in relation R,

​ X1->{ Y1}

​ X2->{Y1 ,Y2, Y3}

​ X3->{ Y1, Y2}

4.R div S is to see whether the image set corresponding to the X attribute in R contains all the values of Y, which can be divided into the following three cases:

	Divisor	Divisor	merchant	remainder	meaning
to be divisible by	X3	Y	n	{}	Table R contains exactly the X of all Y
Division with remainder	X2	Y	n	{Y3}	Table R contains the X of all Y
The divisor set is not contained by the divisor	X1	Y	0	{}	Table R does not contain all Y's X's

Here's how to implement SQL:

As shown in the figure above, select employees who are proficient in Skills from EmpSkills

The above problem can be converted into that the difference set of the elements in the skill table minus the employee's personal technology stack is empty. The SQL is as follows:

SELECT DISTINCT emp
FROM EmpSkills es1
WHERE NOT EXISTS
	(
    SELECT * FROM Skills
    EXCEPT
    SELECT * FROM EmpSkills es2
    WHERE es1.emp=es2.emp
  )

Since not all SQL engines support excel operation, we use NOT EXISTS to implement it.

SELECT DISTINCT emp
FROM EmpSkills es1
WHERE NOT EXISTS
	(
    SELECT * FROM Skills s1
    WHERE NOT EXISTS
    	(
       SELECT * FROM EmpSkills es2
        WHERE es2.emp=es1.emp AND es2.skill=s1.skill
      )
  )

In addition, it can also be implemented with the HAVING clause

SELECT es.emp
FROM EmpSkills es, Skills s
WHERE es.skill=s.skill
GROUP BY es.emp
HAVING COUNT(es.skill)=SELECT COUNT(skill) FROM Skills

The above SQL first finds the intersection of the two tables Skill, and then checks whether the quantity is consistent with the quantity in the Skill table.

Then let's take an advanced step, that is, select employees who are just proficient in Skills from EmpSkills, no more or less, that is, accurate division.

SELECT DISTINCT emp
FROM EmpSkills es1
WHERE NOT EXISTS
	(
    SELECT * FROM Skills s1
    WHERE NOT EXISTS
    	(
       SELECT * FROM EmpSkills es2
        WHERE es2.emp=es1.emp AND es2.skill=s1.skill
      )
  )
  AND NOT EXISTS
  (
  	SELECT * FROM EmpSkills es2
    WHERE NOT EXISTS
    	(
       SELECT * FROM Skills s1
        WHERE es2.emp=es1.emp AND es2.skill=s1.skill
      )
  )

In addition to the NOT EXISTS implementation, let's also look at the implementation with the HAVING clause. We use external connections to complete this operation

SELECT es.emp
FROM EmpSkills es
LEFT OUTER JOIN Skills s
ON es.skill=s.skill
GROUP BY es.emp
HAVING COUNT(es.skill)=SELECT COUNT(skill) FROM Skills 
    AND COUNT(s.skill)=SELECT COUNT(skill) FROM Skills 

UNION operator

This section mainly explains UNION operation through an example

How to judge whether two tables are equal

Method for judging whether two tables are equal
A ∪ B = A ∩ B = A = B A \cup B=A \cap B=A=B A∪B=A∩B=A=B
Equivalent to
C O U N T ( A ∪ B ) = C O U N T ( A ) = C O U N T ( B ) COUNT(A \cup B)=COUNT(A)=COUNT(B) COUNT(A∪B)=COUNT(A)=COUNT(B)

Find equal subsets

Look for suppliers with exactly the same type and quantity of parts

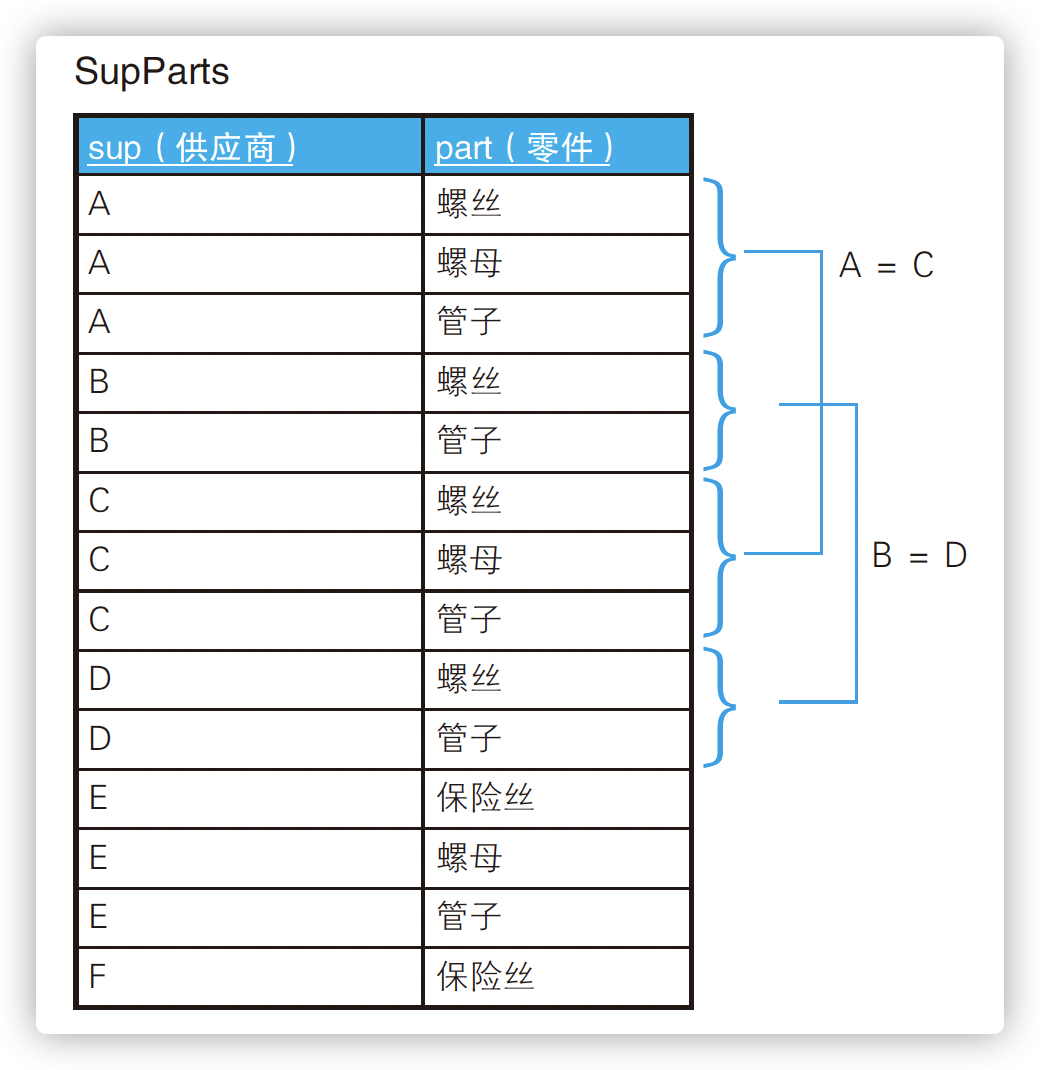
SELECT
  FROM SupParts sp1,
       SupParts sp2
 WHERE sp1.sup>sp2.sup
   AND sp1.part=sp2.part
 GROUP BY sp1.sup,
          sp2.sup
HAVING COUNT(*)=(
        SELECT COUNT(*)
          FROM SupParts sp3
         WHERE sp1.sup=sp3.sup
       )
   AND (
        SELECT COUNT(*)
          FROM SupParts sp4
         WHERE sp2.sup=sp4.sup
       )