Before parsing the code, let's now look at the SRM model.
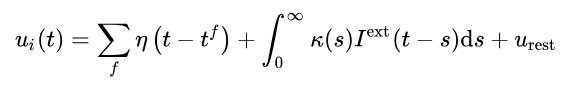
The first function represents the shape a spike should have. Where tf is the time of the last pulse.
In the second function, Iext describes the effect of all presynaptic pulse times on membrane potential.
The third function should be well understood, which is the voltage of a resting potential.
In earlier articles, the SRM model was described as:
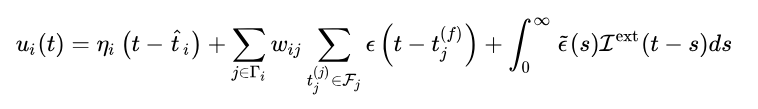
The second is the effect of predecessor neurons on this neuron.
The third item is special
In the general SNN model, it is forcibly stipulated that any input stimulus after the firing of this neuron is directly discarded, but this is too violent and does not conform to the law of biological operation. Therefore, uncle G also arranged a function for the regression of time for this sage. In short, in the sage time, the stimulation received will respond to the membrane potential, but the effect on the membrane potential is very small, which may be less than 1% of that before shooting. Moreover, sage time will reduce the sensitivity of neurons exponentially, that is, the sensitivity of neurons will rise exponentially!
In general, the first item is labeled with the standard emission process potential, the second item represents the effect of all stimuli received before shooting on the potential, and the third item represents the effect of all stimuli received after shooting (SAGE time).
As for the simplified SRM0 neuron.
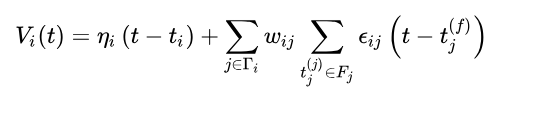
It can be seen that the early SRM model removed the last item, which will also respond to stimuli in refractory period.
The form is like this.
Among them,
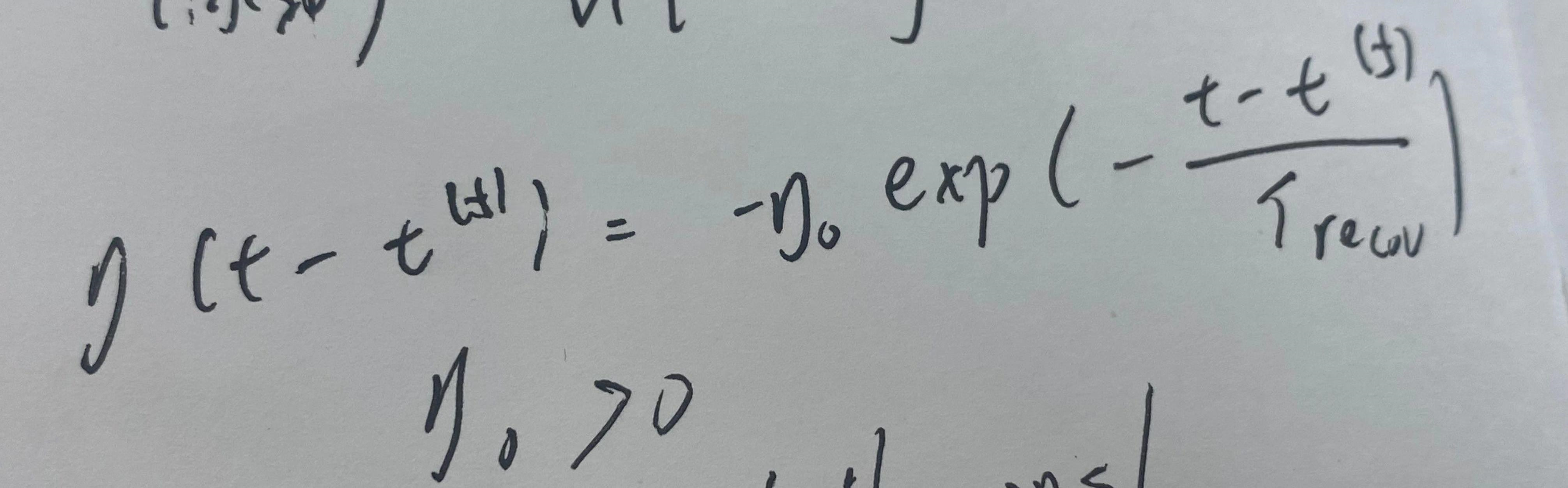
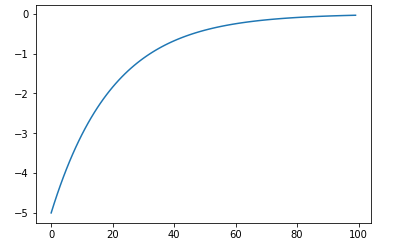
eta function image.
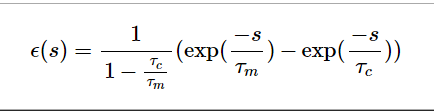
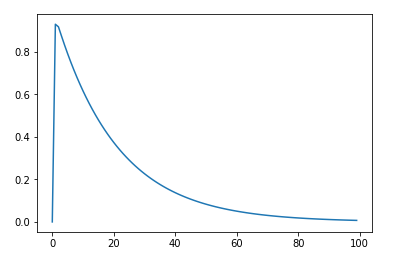
eps function image:
On the code, the code to see more clearly.
import numpy as np
import functools
class SRM:
""" SRM_0 (Spike Response Model) """
#def __init__(self, neurons, threshold, t_current, t_membrane, eta_reset, simulation_window_size=100, verbose=False):
def __init__(self, neurons, threshold=1, t_current=0.3, t_membrane=20, eta_reset=5, simulation_window_size=100, verbose=True):
"""
Neurons can have different threshold, t_current, t_membrane and eta_resets: Set those variables to 1D np.arrays of all the same size.
:param neurons: Number of neurons
:param threshold: Spiking threshold
:param t_current: Current-time-constant (:math:`t_s`) #Current time constant
:type t_current: Float or Numpy Float Array
:param t_membrane: Membrane-time-constant (t_m) #Cell membrane time constant
:param eta_reset: Reset constant
:param simulation_window_size: Only look at the n last spikes #sliding window
:param verbose: Print verbose output to the console
:return: ``None``
"""
# Check user input
try: neurons = int(neurons)
except: raise ValueError("Variable neurons should be int or convertible to int")
# threshold, t_current, t_membrane, and eta_reset are all vector
threshold = np.array(threshold)
t_current = np.array(t_current)
t_membrane = np.array(t_membrane)
eta_reset = np.array(eta_reset)
if not(threshold.shape == t_current.shape == t_membrane.shape == eta_reset.shape): #Threshold input current timing cell membrane timing reset time constant+
raise ValueError("Vector of threshhold, t_current, t_membrane, and eta_reset must be same size")
try: simulation_window_size = int(simulation_window_size)
except: raise ValueError("Variable simulation_window_size should be int or convertible to int")
self.neurons = neurons
self.threshold = threshold
self.t_current = t_current
self.t_membrane = t_membrane
self.eta_reset = eta_reset
self.simulation_window_size = simulation_window_size
self.verbose = verbose
self.cache = {}
self.cache['last_t'] = -1 #Previous timing
self.cache['last_spike'] = np.ones(self.neurons, dtype=float) * -1000000 #Last pulse
self.cache['last_potential'] = np.zeros(self.neurons, dtype=float) #Last moment potential
def eta(self, s):
r"""
Evaluate the Eta function:
.. math:: \eta (s) = - \eta_{reset} * \exp(\frac{- s}{\tau_m})
:label: eta
:param s: Time s
:return: Function eta(s) at time s
:return type: Float or Vector of Floats
"""
return - self.eta_reset*np.exp(-s/self.t_membrane)
@functools.lru_cache()
def eps(self, s):
r"""
Evaluate the Epsilon function:
.. math:: \epsilon (s) = \frac{1}{1 - \frac{\tau_c}{\tau_m}} (\exp(\frac{-s}{\tau_m}) - \exp(\frac{-s}{\tau_c}))
:label: epsilon
Returns a single Float Value if the time constants (current, membrane) are the same for each neuron.
Returns a Float Vector with eps(s) for each neuron, if the time constants are different for each neuron.
:param s: Time s
:return: Function eps(s) at time s
:rtype: Float or Vector of Floats
"""
return (1/(1-self.t_current/self.t_membrane))*(np.exp(-s/self.t_membrane) - np.exp(-s/self.t_current))
@functools.lru_cache()
def eps_matrix(self, k, size):
"""
Returns the epsilon helpermatrix.
:Example:
#>>> eps_matrix(3,5)
[[eps_0(3), eps_0(2), eps_0(1), eps_0(0), eps_0(0)],
[eps_1(3), eps_1(2), eps_1(1), eps_1(0), eps_1(0)]]
Where `eps_0(3)` means the epsilon function of neuron 0 at time 3.
:param k: Leftmost epsilon time
:param size: Width of the return matrix
:return: Epsilon helper matrix
:return type: Numpy Float Array, dimensions: (neurons x size)
"""
matrix = np.zeros((self.neurons, size), dtype=float)
for i in range(k):
matrix[:, i] = self.eps(k-i)
return matrix
def check_spikes(self, spiketrain, weights, t, additional_term=None):
"""
Simulate one time step at time t. Changes the spiketrain in place at time t!
Return the total membrane potential of all neurons.
:param spiketrain: Spiketrain (Time indexing begins with 0)
:param weights: Weights
:param t: Evaluation time
:param additional_term: Additional potential that gets added before we check for spikes (For example for extern voltage)
:return: total membrane potential of all neurons at time step t (vector), spikes at time t
"""
# Check correct user input
if type(spiketrain) != np.ndarray:
raise ValueError("Spiketrain should be a numpy array")
if type(weights) != np.ndarray:
raise ValueError("Weights should be a numpy matrix")
if additional_term != None and type(additional_term) != np.ndarray:
raise ValueError("Additional_term should be a numpy array")
try: t = int(t)
except: raise ValueError("Variable t should be int or convertible to int")
if t < 0:
raise ValueError("Time to be simulated is too small")
if t >= spiketrain.shape[1]: #spiketrain.shape[1] 'return no of column in each row '
raise ValueError("Spiketrain too short (0ms -- %dms) for simulating time %d" % (spiketrain.shape[1]-1, t))
if weights.shape[0] != self.neurons or self.neurons != weights.shape[1]:
raise ValueError("Weigths should be a quadratic matrix, with one row and one column for each neuron")
if spiketrain.shape[0] != self.neurons:
raise ValueError("Spikes should be a matrix, with one row for each neuron")
if additional_term != None and additional_term.shape[0] != self.neurons:
raise ValueError("Additional_term should be a vector with one element for each neuron")
if additional_term != None and len(additional_term) == 2 and additional_term.shape[1] != 1:
raise ValueError("Additional_term should be a vector with one element for each neuron")
# Work on a windowed view
spiketrain_window = spiketrain[:, max(0, t+1-self.simulation_window_size):t+1]
# Retrieve necessary simulation data from cache if possible
if self.cache['last_t'] == -1 or self.cache['last_t'] == t - 1:
last_spike = self.cache['last_spike']
last_potential = self.cache['last_potential']
else:
last_spike = t - np.argmax(spiketrain_window[:, ::-1], axis=1)
# TODO find a way to calculate last_potential (recursive call to check_spikes is not a good option)
last_potential = np.zeros(self.neurons)
neurons, timesteps = spiketrain_window.shape
epsilon_matrix = self.eps_matrix(min(self.simulation_window_size, t), timesteps)
# Calculate current
incoming_spikes = np.dot(weights.T, spiketrain_window) #Matrix multiplication
incoming_potential = np.sum(incoming_spikes * epsilon_matrix, axis=1)
total_potential = self.eta(np.ones(neurons)*t - last_spike) + incoming_potential
# Calculate current end
# Add additional term (user-defined)
if additional_term != None:
total_potential += additional_term
# Any new spikes? Only spike if potential hits the threshold from below.
neurons_high_current = np.where((total_potential > self.threshold) & (last_potential < self.threshold))
spiketrain[neurons_high_current, t] = True
# Update cache (last_spike, last_potential and last_t)
spiking_neurons = np.where(spiketrain[:, t])
self.cache['last_spike'][spiking_neurons] = t
self.cache['last_potential'] = total_potential
self.cache['last_t'] = t
if self.verbose:
print("SRM Time step", t)
print("Incoming current", incoming_potential)
print("Total potential", total_potential)
print("Last spike", last_spike)
print("")
return total_potential
if __name__ == "__main__":
srm_model = SRM(neurons=3, threshold=1, t_current=0.3, t_membrane=20, eta_reset=5, verbose=True) #Define an SRM neuron
models = [srm_model]
for model in models:
print("-"*10)
if isinstance(model, SRM):
print('Demonstration of the SRM Model')
s = np.array([[0, 0, 1, 0, 0, 0, 1, 1, 0, 0],
[1, 0, 0, 0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
#w = np.array([[0, 0, 3.8], [0, 0, 1.78], [0, 0, 0]])
w = np.array([[0, 0, 1], [0, 0, 1], [0, 0, 0]]) #weight
#w = np.random.random((3,3))
neurons, timesteps = s.shape
for t in range(timesteps):
total_current = model.check_spikes(s, w, t)
print("Spiketrain:\n", s)