Original title website
For some reason, this website will not be accessible
1045. Medicine Collection - original website
Title Description
Chenchen is a gifted and intelligent child. His dream is to become the greatest doctor in the world. To this end, he wanted to learn from the most prestigious doctors nearby. The doctor gave him a difficult problem in order to judge his qualifications. The doctor took him to a cave full of herbs and said to him: "Child, there are some different herbs in this cave. It takes some time to pick each one, and each one has its own value. I will give you a period of time, during which you can pick some herbs. If you are a smart child, you should be able to maximize the total value of the herbs you pick." If you are Chenchen, can you finish this task?
format
Input format
The first line of input has two integers T ( 1 ≤ T ≤ 1000 ) T(1\le T\le1000) T(1 ≤ t ≤ 1000) and M ( 1 ≤ M ≤ 100 ) M(1\le M\le100) M(1 ≤ m ≤ 100), separated by a space, T T T represents the total time that can be used to collect medicine, M M M stands for the number of herbs in the cave. Next M M M lines, each line includes two 1 1 1 to 100 100 Between 100 (inclusive) 1 1 1 and 100 100 100), representing the time of picking a herb and the value of the herb respectively.
Output format
The output includes a line, which contains only an integer, indicating the maximum total value of herbs that can be collected within a specified time.
Sample
sample input
70 3 71 100 69 1 1 2
sample output
3
Tips
about
30
%
30\%
30% of the data,
M
≤
10
M\le10
M≤10;
For all data,
M
≤
100
M\le100
M≤100.
Problem solving ideas
This question is
D
P
DP
DP (dynamic programming) is a classic example of knapsack problem. Solutions to basic knapsack problems are based on the following figure:
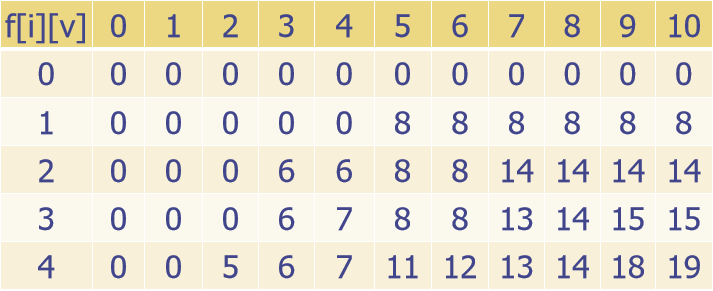
This graph is entered as
10 4 5 8 3 6 4 7 2 5
The results of the. Dynamic programming array
f
[
i
]
[
v
]
f[i][v]
The number of f[i][v] indicates the front
i
i
i herbs at time
v
v
v is the maximum number of herbs that can be collected. However, the above figure is wrong, and the correct one should be as follows:
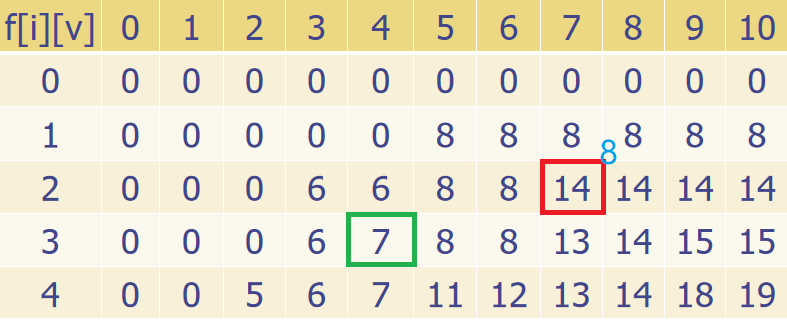
The red box in the above figure is the wrong place, blue“
8
8
8 "is the correct number to fill in. Less nonsense, let's talk about how this picture comes from: let's take a chestnut, the number in the green box above“
7
7
7 "comes from this: first of all, consider not selecting to collect the current second data
i
i
i herbs (now
3
3
3) The situation, that is
f
[
i
−
1
]
[
v
]
f[i-1][v]
f[i−1][v]; Secondly, consider that time is sufficient and select the current second
i
i
i herbs (now
3
3
3) In other words, the time should be divided into two parts. One part is to pick the current herb (now
4
4
4) The other part is for the maximum number of herbs before picking (now
6
6
6) , then
f
[
i
−
1
]
[
v
−
t
[
i
]
]
+
w
[
i
]
f[i-1][v-t[i]]+w[i]
f[i − 1][v − t[i]]+w[i] (where
t
[
i
]
t[i]
t[i] means picking the second
i
i
Time required for i herbs,
w
[
i
]
w[i]
w[i] stands for the second
i
i
Value of i herbs).
Code
Forward push method
#include<iostream>
#include<iomanip>
#include<istream>
#include<ostream>
#include<ios>
#include<set>
#include<fstream>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<map>
#include<queue>
#define maxn 1000
using namespace std;
int t, m, q[maxn + 1], w[maxn + 1], s[maxn + 1][maxn + 1];
void init()
{
cin>>t>>m;
for (int i = 1; i <= m; i ++) cin>>q[i]>>w[i];
}
void comp()
{
for (int i = 1; i <= m; i ++) for (int j = 1; j <= t; j ++) // DP (dynamic programming) cycle
{
if (q[i] <= j) s[i][j] = max(s[i - 1][j], s[i - 1][j - q[i]] + w[i]);
else s[i][j] = s[i - 1][j]; // Push forward, using a two-dimensional array
}
}
void oput()
{
cout<<s[m][t]; // Output results
}
int main()
{
init();
comp();
oput();
return 0;
}
Inverse method
#include<iostream>
#include<iomanip>
#include<istream>
#include<ostream>
#include<ios>
#include<set>
#include<fstream>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<map>
#include<queue>
#define maxn 1000
using namespace std;
int t, m, q[maxn + 1], w[maxn + 1], s[maxn + 1];
void init()
{
cin>>t>>m;
for (int i = 1; i <= m; i ++) cin>>q[i]>>w[i];
}
void comp()
{
for (int i = 1; i <= m; i ++) for (int j = t; j >= 1; j --) // DP (dynamic programming) cycle
{
if (q[i] <= j) s[j] = max(s[j], s[j - q[i]] + w[i]); // Backstepping, using a one-dimensional array
}
}
void oput()
{
cout<<s[t]; // Output results
}
int main()
{
init();
comp();
oput();
return 0;
}
Push + number
#include<iostream>
#include<iomanip>
#include<istream>
#include<ostream>
#include<ios>
#include<set>
#include<fstream>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<map>
#include<queue>
#define maxn 1000
using namespace std;
int t, m, q[maxn + 1], w[maxn + 1], s[maxn + 1][maxn + 1], e[maxn + 1];
void init()
{
cin>>t>>m;
for (int i = 1; i <= m; i ++) cin>>q[i]>>w[i];
}
void comp()
{
for (int i = 1; i <= m; i ++) for (int j = 1; j <= t; j ++) // DP (dynamic programming) cycle
{
if (q[i] <= j) s[i][j] = max(s[i - 1][j], s[i - 1][j - q[i]] + w[i]);
else s[i][j] = s[i - 1][j]; // Push forward, using a two-dimensional array
}
for (int i = m; i >= 1; i --)
{
if (s[i][t]!=s[i-1][t]) // Indicates that a new herb is currently selected
{
e[i] = 1;
}
}
}
void oput()
{
cout<<s[m][t];
cout<<endl;
for (int i = 1; i <= m; i ++) if (e[i]) cout<<i<<" ";
}
int main()
{
init();
comp();
oput();
return 0;
}
Push + roll
#include<iostream>
#include<iomanip>
#include<istream>
#include<ostream>
#include<ios>
#include<set>
#include<fstream>
#include<sstream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<map>
#include<queue>
#include<vector>
#define maxn 1000000
using namespace std;
int n, m, a[maxn + 1], b[maxn + 1], t[maxn + 1], s[maxn + 1];
void init()
{
cin>>n>>m;
for (int i = 1; i <= m; i ++) cin>>t[i]>>s[i];
}
void dp()
{
for (int i = 1; i <= m; i ++) // DP (dynamic programming) cycle
{
memcpy(b, a, sizeof(a)); // Scroll array
for (int j = t[i]; j <= n; j ++) a[j] = max(b[j], b[j - t[i]] + s[i]);
}
}
void oput()
{
cout<<a[n]; // Output results
}
int main()
{
init();
dp();
oput();
return 0;
}
be accomplished ∼ \sim ∼