Polygon area

Description

Jerry, a middle school student, is intoxicated with mathematical research. His problems may be too simple for experts, but as a 15-year-old amateur, he does very well. He is so keen on thinking about mathematical problems that he easily learns to try mathematical methods to solve problems. One day, He saw a piece of paper on the table. His four-year-old sister Mary drew some lines in the center. Those lines just formed a concave polygon, as shown below:

"Great," he thought, "these polygons look regular. I've learned how to calculate the area of triangles, rectangles and circles. I'm sure I can find a way to calculate these figures. " He did. First, he marks the coordinates of the vertices of the polygon. As shown in Figure 2. Then he effortlessly obtained the result of 0.75.

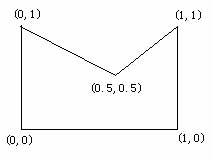
Of course, he will not be satisfied with solving such a simple problem. "Well, if there is any polygon on the paper, how should we calculate its area?" He asked himself. But he has never found a general method to calculate the area of polygons. He clearly understood that with his ability he could not find the answer. So he asked you for advice. He will appreciate your kind help.

Input

The first line is an integer n, representing the number of vertices of the graph (1 < = n < = 1000)
The next n lines, each with a pair of real numbers, represent the vertex coordinates (xi,yi). The shape of each sample is connected by the first vertex to the second vertex, the second vertex to the third vertex... And finally the nth vertex to the first vertex to form a closed polygon.

Output

Output drawing area or string "Impossible"
If the figure is a polygon, calculate its area (accurate to two decimal places). If the input vertices cannot form a polygon (that is, one edge intersects an edge that is not connected to another edge, for example, in the shape of four segments, the first segment intersects the third segment), output "Impossible". Indicates that the shape cannot be a polygon. If the number of vertices is not enough to form a closed polygon, you can also output "invisible"

Hint

GDKOI2002-5
For finding the area of a polygon (whether concave or convex), it is also possible to cross product. Let the polygon vertices be A1,A2,A3,..., AN, then the polygon area is:
A1A2A1A3+A1A3A1A4+...+A1An-1*AN

sample input

1

5
0 0
0 1
0.5 0.5
1 1
1 0

2

4
0 0 
0 1
1 0
1 1

sample output

1

0.75

2

Impossible

Problem solving ideas

reference resources [51nod 1264] intersection of line segments (computational geometry) and P2785 Physics 1 (phsic1) - magnetic flux (computational geometry)

AC code

#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int n;
double ans,x[1005],y[1005];
struct node
{
	double x,y;
}a[5];
double cj(node x,node y,node z)
{
	return (x.x-z.x)*(y.y-z.y)-(x.y-z.y)*(y.x-z.x);
}
bool check(node x,node y,node z)
{
	if(z.x>=min(x.x,y.x)&&z.x<=max(x.x,y.x)&&z.y>=min(x.y,y.y)&&z.y<=max(x.y,y.y))return 1;
	return 0;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%lf%lf",&x[i],&y[i]);
	if(n<3){printf("Impossible");return 0;}
	for(int i=1;i<n;i++)
		for(int j=i+2;j<=n;j++)
			{
				if(i==1&&j==n)continue;
				int t=j+1;
				if(t>n)t=1;
				a[1]=(node){x[i],y[i]};
				a[2]=(node){x[i+1],y[i+1]};
				a[3]=(node){x[j],y[j]};
				a[4]=(node){x[t],y[t]};
				int ok=0;
				if(cj(a[3],a[4],a[1])*cj(a[3],a[4],a[2])<0&&cj(a[1],a[2],a[3])*cj(a[1],a[2],a[4])<0)ok=1;
				if(!cj(a[1],a[2],a[3])&&check(a[1],a[2],a[3]))ok=1;
				if(!cj(a[1],a[2],a[4])&&check(a[1],a[2],a[4]))ok=1;
				if(!cj(a[3],a[4],a[1])&&check(a[3],a[4],a[1]))ok=1;
				if(!cj(a[3],a[4],a[2])&&check(a[3],a[4],a[2]))ok=1;
				if(ok){printf("Impossible");return 0;}
			}
	for(int i=1;i<n;i++)
		ans+=(x[i]*y[i+1]-x[i+1]*y[i])/2.0;
	ans+=(x[n]*y[1]-x[1]*y[n])/2.0;
	printf("%.2lf",abs(ans));
	return 0;
} 

thank you