Stack and queue

Stacks and queues are special linear tables. That is, elements other than the first element and the last element have only one predecessor element and one successor element.
The difference is that the insertion and deletion of linear tables are not limited, while the insertion and deletion of stacks and queues have some special requirements. The answers are given below.

stack

1. Similar to the clip structure, only one end is allowed to insert and delete.
2. The end that allows insertion and deletion is called the top of the stack and the other end is called the low of the stack.
3. Insertion is called stacking in or out, and deletion is called out or out of stack.
4. The elements that enter the stack last always exit the stack first.

Abstract data type of stack

1. Operation set

• push(Object obj): push the data element obj onto the stack
• Out of stack pop(): out of stack top elements
• Get top data element getTop(): get the top data element
• Non empty stack notEmpty(): returns true for non empty stack. Otherwise, vice versa.

1. Abstract data type interface

public interface Stack{
	public void push(Object obj)throws Exception;
	public void pop()throws Exception;
	public Object getTop()throws Exception;
	public boolean notEmpty()throws Exception;
}

1. Stack access characteristics

• Insert the element before moving the pointer
• Move the pointer before exiting the element.

Sequential stack

public class SeqStack implements Stack {
	/*
	 * 1,defaultSize:Default size
	 * 2,top: Stack top position
	 * 3,stack: Stack array object
	 * 4,maxStackSize: Maximum storage data element
	 */
	final int defaultSize = 10;
	int top;
	Object[] stack;
	int maxStackSize;
	public SeqStack() {
		initiate(defaultSize);
	}
	public SeqStack(int i) {
		initiate(i);
	}
	public void initiate(int sz) {
		maxStackSize = sz;
		top = 0;
		stack = new Object[sz];
	}
	@Override
	public void push(Object obj) throws Exception {
		// Push 
		if(top == maxStackSize) {
			throw new Exception("Stack full!");
		}
		stack[top] = obj;
		top++;
	}

	@Override
	public Object pop() throws Exception {
		// Back stack
		if(top == 0) {
			throw new Exception("Stack is empty!");
		}
		top--;
		return stack[top];
	}

	@Override
	public Object getTop() throws Exception {
		// Get stack top element
		return stack[top-1];
	}

	@Override
	public boolean notEmpty() throws Exception {
		// Non empty stack
		return top>0;
	}

}

Chain stack

• The chained stack requires a node class as follows:

public class Node{
   /*
	*1,next Point to next node
	*2,data Store elements
	*/
	Node next;
	Object obj;
	//Construction method for head node
	public Node(Node nextval){
		next = nextval
	}
	//Construction method for other nodes
	public Node(Node nextval,Object obj){
		next = nextval;
		data = obj;
	}
	public Node getNext(){
		return next;	
	}
	public void setNext(Node nextval){
		next = nextval;
	}
	public Object getElement(){
		return data;	
	}
	public void setElement(Object obj){
		data = obj;
	}
	
}

• Chain queue

	public class LinStack implements Stack {
	/*
	 * 1,head //Stack top node
	 * 2,size //Number of nodes
	 */
	Node head;
	int size;
	public LinStack() {
		head = null;
		size = 0;
	}
	@Override
	public void push(Object obj) throws Exception {
		// Push 
		head = new Node(obj,head);
		size++;
	}

	@Override
	public Object pop() throws Exception {
		// Back stack
		if(size == 0) {
			throw new Exception("Stack is empty");
		}
		Object obj = head.getElement();
		head = head.getNext();
		size--;
		return obj;
	}

	@Override
	public Object getTop() throws Exception {
		// Get stack top element
		return head.getElement();
	}

	@Override
	public boolean notEmpty() throws Exception {
		// Non empty stack
		return head != null;
	}

}

Application of stack

Bracket matching problem

In common arithmetic, the matching order of the right bracket and the left bracket is adjusted well, which conforms to the characteristics of last in, first out of the stack. Therefore, the problem of judging bracket matching can be completed with the help of stack.

1. When the right bracket is scanned, judge whether the element at the top of the stack is the left bracket. If not, the order of the brackets does not match.
2. When the stack is empty when the right bracket is scanned, the right bracket is more than the left bracket.
3. When the scan is completed and the stack is not empty, the left bracket is more than the right bracket.
4. When the scan is complete and the stack is empty, the left and right parentheses match correctly.

public class Exp {
	Stack stack;
	//Receive a character array composed of parentheses to determine whether it matches
	public void expIsCorrent(String[] exp) {
		stack = new LinStack();
		int length = exp.length;
		try {
			for(int i = 0;i<length;i++) {
				//Store all encountered left parentheses on the stack
				if((exp[i].equals("(")) 
					|| (exp[i].equals("{"))
					|| (exp[i].equals("["))){
						stack.push(exp[i]);
				}
				//If the left bracket is not encountered, judge whether the right bracket matches the bracket at the top of the heap
				else if((exp[i].equals(")")
						&& stack.notEmpty()
						&& stack.getTop().equals("("))){
					stack.pop();
				}
				else if((exp[i].equals(")")
						&& stack.notEmpty()
						&& !stack.getTop().equals("("))){
					throw new Exception("Bracket mismatch");
				}
				else if((exp[i].equals("]")
						&& stack.notEmpty()
						&& stack.getTop().equals("["))){
					stack.pop();
				}
				else if((exp[i].equals("]")
						&& stack.notEmpty()
						&& !stack.getTop().equals("["))){
					throw new Exception("Bracket mismatch");
				}
				else if((exp[i].equals("}")
						&& stack.notEmpty()
						&& stack.getTop().equals("{"))){
					stack.pop();
				}
				else if((exp[i].equals("}")
						&& stack.notEmpty()
						&& !stack.getTop().equals("{"))){
					throw new Exception("Bracket mismatch");
				}
				else if((exp[i].equals(")"))
						|| (exp[i].equals("}"))
						|| (exp[i].equals("]"))) {
					throw new Exception("There are more right parentheses than left parentheses");
				}
			}
			if(stack.notEmpty()) {
				System.out.println("There are more left parentheses than right parentheses");
			}else {
				System.out.println("The brackets match correctly");
			}
		}catch(Exception e) {
			System.out.println(e.getMessage());
		}
	}
}

Expression evaluation

Infix expressions are always converted into suffix expressions for operation in computers. For example, when A+(B-C/D)*E is converted into a suffix expression, it is ABCD/-*E +. Suffix expressions have the following characteristics:

1. The operand order of suffix expression and prefix expression is the same, and the operator order is different.
2. The operator order of the suffix expression is its execution order.
3. When processing the suffix expression, scan the suffix expression from left to right. When an operator is encountered, the first two operands will be operated. Until the expression is processed.

public class PostExpression {
	public static void postExp(LinStack s) throws Exception{
		/*
		 * ch expression
		 * x1 The previous element at the top of the stack, or used to save the calculation results
		 * x2 Stack top element
		 * b Received characters
		 */
		char ch;
		int x1,x2,b=0;
		System.out.println("Enter suffix expression");
		/*
		 * 	Circulation has the following meanings
		 * 	1.First, enter the infix expression at once
		 * 	2.Receive the input characters one by one, convert them into char and store them in ch
		 * 	3.If the last one is #, the operation ends.
		 */
		while((ch = (char)(b = System.in.read()))!='#') {
			//Judge whether the received character is a number, and if so, put it on the stack
			if(Character.isDigit(ch)) {
				s.push(new Integer(Character.toString(ch)));
			}else {
				//If the character received is not a number, it is an operator
				//Back the stack to two numbers for operation
				x2 = ((Integer)s.pop()).intValue();
				x1 = ((Integer)s.pop()).intValue();
				switch(ch) {
				//Judgment operator category
				case '+':
					x1 += x2;
					break;
				case '-':
					x1 -= x2;
					break;
				case '*':
					x1 *= x2;
					break;
				case '/':
					if(x2 == 0) {
						throw new Exception("Divisor is 0");
					}else {
						x1 /= x2;
						break;
					}
					
				}
				//After the operation is completed, put the operation result on the stack and wait for the next operation
				s.push(new Integer(x1));
			}
		}
		//At the end of the cycle, the final result is output
		System.out.println("Expression evaluation result:"+s.pop());
	}
	public static void main(String args[]) {
		LinStack stack = new LinStack();
		try {
			postExp(stack);
		}catch(Exception e) {
			System.out.println(e.getMessage());
		}
	}
}

queue

1. Similar to the queuing structure, only one end is allowed to insert and the other end is allowed to delete.
2. Allowing insertion is called the tail of the team and the other end is called the head of the team.
3. Insertion is called in queue and deletion is called out queue.
4. Elements that enter the stack first always exit the stack first.

Queue abstract data type

1. Operation set

• Queue append(Object obj): inserts the data element obj into the end of the queue
• Out of queue delete(): out of queue the queue header element
• Get queue header data element getFront(): get queue header data element
• Non empty queue notempty(): non empty queue

1. Abstract data type interface

public interface Queue{
	public void append(Object obj)throws Exception;
	public Object delete()throws Exception;
	public Object getFront()throws Exception;
	public boolean notEmpty();
}

1. Queue characteristics

• front stands for the head of the team and rear stands for the tail
• When leaving the queue, move the front first and then delete the element
• When queuing, insert the element first and then move the rear

Sequential queue

Generally, the front of the queue points to the head of the queue and the rear points to the tail of the queue. The structure is as follows. From the figure, we can find that the general queue has the following problems.

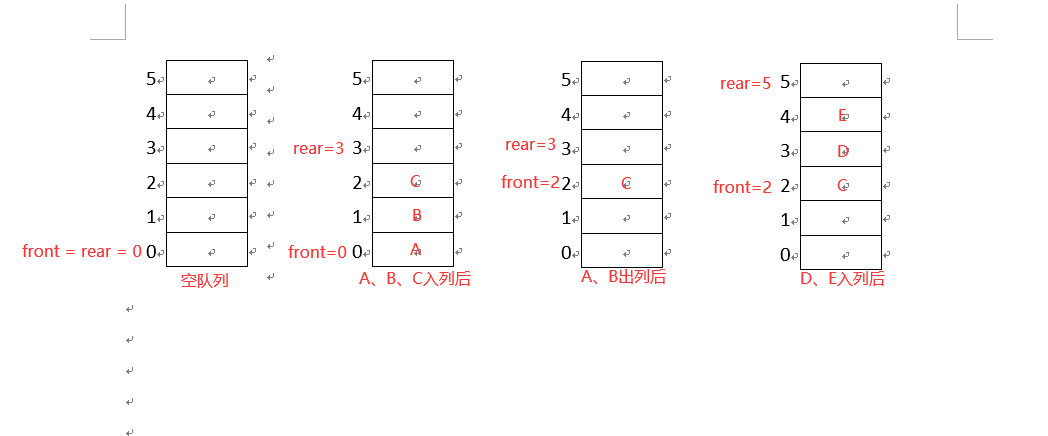
1. Team empty, team full, judge the problem

When front=rear=0, we can judge that the queue is empty at this time
When front = 0 and rear = 6, we can judge that the queue is full.
But is it true that the queue is full?

1. False overflow problem

The queue only allows the deletion of elements at the head of the queue and the insertion of elements at the end of the queue. In the fourth case in the figure, only one more element can be inserted. However, although there are two empty positions, they cannot be inserted because the rear does not point to where. This creates a false overflow problem.

1. The resulting circular queue is as follows

Sequential cyclic queue

1. Cyclic queue principle

The false removal problem is that the value of rear and the value of front cannot flexibly point to the position they should point to. However, if the values of rear and front reach maxSize-1, add 1 and the remainder will automatically point to 0, then this problem can be solved.
It is realized by taking remainder. For example: maxSize=6, when rear=5, rear= (rear+1)%6 = 0.

1. Team leader and tail judgment

Design a counter count. When count=0, the queue is empty. When count > 0 & & front = = rear, the queue is full.

public class SeqQueue implements Queue {
	/**
	 * 1. defaultSize:Default queue size
	 * 2. front: Point to the head of the team
	 * 3. rear: Point to the end of the team
	 * 4. count: Number of contained elements
	 * 5. maxSize: Maximum number of elements
	 * 6. data: Store elements
	 */
	
	final int defaultSize = 10;
	int front;
	int rear;
	int count;
	int maxSize;
	Object[] data;
	public SeqQueue() {
		initiate(defaultSize);
	}
	public SeqQueue(int sz) {
		initiate(sz);
	}
	public void initiate(int sz) {
		maxSize = sz;
		data = new Object[sz];
		front = rear = 0;
		count = 0;
	}
	@Override
	public void append(Object obj) throws Exception {
		// Before entering the queue, you need to judge whether the queue is full
		if(count>0 && front == rear) {
			throw new Exception("The queue is full");
		}
		data[rear] = obj;
		rear = (rear+1)%maxSize;
		count++;
	}

	@Override
	public Object delete() throws Exception {
		// To get out of the queue, you need to judge whether the queue is empty
		if(count == 0 ) {
			throw new Exception("The queue is empty");
		}
		Object obj = data[front];
		front = (front+1)%maxSize;
		count --;
		return obj;
	}

	@Override
	public Object getFront() throws Exception {
		// Take team header element
		return data[front];
	}

	@Override
	public boolean notEmpty() {
		// Non empty queue
		return count != 0;
	}

}

Chain queue

1. Node class is required
2. Because it is chain, it has no size.

public class LinQueue implements Queue {
	Node front;
	Node rear;
	int count;
	public LinQueue() {
		count = 0;
		front = rear = null;
	}
	@Override
	public void append(Object obj) throws Exception {
		Node newNode = new Node(obj,null);
		//If it is not the first insertion, you need to link the previous element to the newly inserted element
		if(rear != null) {
			rear.setNext(newNode);
		}
		//Place element at end of queue
		rear = newNode;
		//The first insertion of the head and tail of the team points to the same element
		if(front == null) {
			front = newNode;
		}
		count++;
	}

	@Override
	public Object delete() throws Exception {
		//When the queue is dequeued, judge whether the queue is empty
		if(count == 0) {
			throw new Exception("The queue is empty");
		}
		Node node = front;
		//Directly overhead the team head element and take the next element as the team head
		front = front.getNext();
		count--;
		return node.getElement();
	}

	@Override
	public Object getFront() throws Exception {
		// Take the head of the team
		if(count == 0 ) {
			throw new Exception("The queue is empty");
		}
		return front.getElement();
	}

	@Override
	public boolean notEmpty() {
		// Non empty queue
		return count != 0;
	}

}

Priority queue

No longer only from the queue head out of the queue, but using priority out of the queue. Starting from the head of the queue, the one with the highest priority will be out of the queue first.

characteristic:

1. Create a priority element class, which contains two attributes: element and priority.
2. Find out the element with the highest priority from the queue, and move each element after the element forward one bit. Therefore, you do not need to set up a circular queue.

Sequential priority queue

1. New class with priority

	class Element{
	private Object elem;//data elements
	private int priority;//priority
	Element(Object obj,int i){
		elem = obj;
		priority = i;
	}
	Element(Object obj){
		elem = obj;
		priority = 10;//Default priority setting 10
	}
	public Object getElem() {
		return elem;
	}
	public void setElem(Object elem) {
		this.elem = elem;
	}
	public int getPriority() {
		return priority;
	}
	public void setPriority(int priority) {
		this.priority = priority;
	}
	
}

1. Sequential priority queue

public class SeqPQueue implements Queue{
	final int defaultSize = 10;
	int front;
	int rear;
	int count;
	int maxSize;
	Element[] data;
	public SeqPQueue() {
		initiate(defaultSize);
	}
	public SeqPQueue(int sz) {
		initiate(sz);
	}
	public  void initiate(int sz) {
		maxSize = sz;
		data = new Element[maxSize];
		count = 0;
		front = 0;
		count = 0;
	}
	@Override
	public void append(Object obj) throws Exception {
		// Queue
		if(count >= maxSize) {
			throw new Exception("The queue is full");
		}
		data[rear] = (Element)obj;
		rear++;
		count++;
		
	}

	@Override
	public Object delete() throws Exception {
		// Out of queue
		if(count == 0 ) {
			throw new Exception("The queue is empty");
		}
		Element min = data[0];//Assume minimum priority
		int minIndex = 0;//Assume minimum priority element location
		//Find the location with the lowest priority
		for(int i = 0;i<count;i++) {
			if(data[i].getPriority() < min.getPriority()) {
				min = data[i];
				minIndex = i;
			}	
		}
		//Move the elements following the priority element forward one position at a time
		for(int i = minIndex+1;i<count;i++) {
			data[i-1] = data[i];
		}
		rear = rear-1;
		count--;
		return min.getElem();
	}

	@Override
	public Object getFront() throws Exception {
		// Take the head of the team
		if(count == 0) {
			throw new Exception("The queue is empty");
		}
		return data[front];
	}

	@Override
	public boolean notEmpty() {
		// Non empty queue
		return count != 0;
	}

}

@syl 2021/08/19 17:51 Thursday fine