May every time I remember, I don't feel guilty about my life. —— Guo Xiaochuan

Stack, referred to as LIFO in English Last In First Out, follows the principle of "last in first out". Contrary to "queue", it adds and deletes elements at the head of the stack. If there are no elements in the stack, it is called empty stack.

Author's Profile: May Jun, Nodejs Developer, post-90s youth who love technology and like to share, Public No. Nodejs Technology Stack, Github Open Source Project https://www.nodejs.red

Stack Introduction

There are also many examples in real life scenarios, such as plate stacking, from the top one to the top one, when taking away from the top one, it is impossible to take directly from the bottom, as shown in the figure below.

This is also a typical application of stack. Two characteristics of stack can also be summarized through this example.

1. Access data only from the top of the stack
2. Data Access Compliance with the First in First Out Principle

Operation mechanism of stack

As for the concept of stack, we should have a preliminary understanding through the previous study. Here we make a further analysis of the operation mechanism of stack by implementing a stack from scratch. Let's see what steps we need to implement the stack.

1. Constructor(capacity): Initialize stack memory space and set stack capacity
2. isEmpty(): Check if the stack is empty and if there are elements
3. isOverflow(): Check if the stack space is full and if it is full, it cannot be put on the stack.
4. enStack(element): The top of the stack is placed on the stack. First, determine whether the stack is full or not.
5. deStack(): The top of the stack is out of the stack. First, determine whether the stack element is empty.
6. len(): Length of existing elements in stack space
7. clear(): Clear stack elements, and memory space is reserved
8. destroy(): Destroy the stack and reclaim memory at the same time. (Usually high-level languages have automatic reclaim mechanisms, such as C, which requires manual reclaim)
9. traversing(): traversing output stack elements

Initialize stack space

In the constructor of the constructor, a declaration is made that the capacity initializes the stack space and initializes the top of the stack at the same time, while the bottom does not need to be concerned about always being 0.

/**
 * 
 * @param { Number } capacity Stack space capacity
 */
constructor(capacity) {
    if (!capacity) {
        throw new Error('The capacity field is required!');
    }

    this.capacity = capacity;
    this.stack = new Array(capacity);
    this.top = 0; // Initialization stack top 0 
}

Whether stack space is empty or not

Defines whether the isEmpty() method returns empty stack space, and judges it according to the top position of the top stack.

isEmpty() {
    return this.top === 0 ? true : false;
}

Stack space overflow check

The isOverflow() method is defined to determine whether the stack space is overflowed or not, based on the location of the top of the stack and the space capacity of the stack.

isOverflow() {
    return this.top === this.capacity;
}

Push

enStack(element) method is defined for stacking operation. Element is a parameter passed into the stack. Before entering the stack, it is judged whether the stack is full or not. When the stack is not full, stack operation can be carried out. Finally, stack position is operated by +.

/**
 * Push
 * @param { * } element Stack element
 */
enStack(element) {
    if (this.isOverflow()) {
        throw new Error('The stack is full');
    }

    this.stack[this.top] = element;
    this.top++;
}

Stack out

Define the enStack(element) method for stack-out operation. First, judge whether the stack space is empty or not, pay attention to the stack location here. Because the element will be ++ operation after it is put on the stack, the current stack location must be no element at the time of stack-out, so we need to Do-operation first.

deStack() {
    if (this.isEmpty()) {
        throw new Error('The stack is empty');
    }

    this.top--;
    return this.stack[this.top];
}

Stack element length

This good judgment is based on the top location of the stack.

len() {
    return this.top;
}

Clear stack elements

There are several implementations. You can also initialize the stack space or set the top stack position to zero.

clear() {
    this.top = 0;
}

Stack destruction

In some high-level languages, there will be garbage collection mechanisms, such as JS, as long as the current object no longer holds references, the next garbage collection will be recycled. I don't know. Look at what I wrote before. Node.js Memory Management and V8 Garbage Recycling Mechanism

destroy() {
    this.stack = null;
}

Stack element traversal

The traversing(isBottom) method is defined to traverse the elements of the stack. The default is top traversal, and the isBottom parameter is true to traverse from the bottom.

traversing(isBottom = false){
    const arr = [];

    if (isBottom) {
        for (let i=0; i < this.top; i++) {
            arr.push(this.stack[i])
        }
    } else {
        for (let i=this.top-1; i >= 0; i--) {
            arr.push(this.stack[i])
        }
    }

    console.log(arr.join(' | '));
}

Do some testing

Do the next test to see the stack, stack, traversal operation, other functions you can practice in the process of practice.

const s1 = new StackStudy(4);

s1.enStack('Nodejs'); // Push
s1.enStack('technique');
s1.enStack('art');
s1.enStack('Stack');
s1.traversing() // Stack | Skill | Techniques | Nodejs
console.log(s1.deStack()); // Exit Stack - > Stack
s1.traversing() // Nodejs
s1.traversing(true) // Traveling from the bottom of the stack: Nodejs | Techniques | Techniques

Here is a diagram showing the process of stacking and exiting the above programs.

The source code address of the stack's operating mechanism is as follows:

https://github.com/Q-Angelo/project-training/tree/master/algorithm/stack.js

JavaScript Array Implementation Stack

The array function provided in JavaScript can realize a simple stack. It is also very convenient to use. Familiarity with relevant API s is enough. Now let's look at the implementation of stacking and stacking based on JS arrays.

The above pictures show the process of stack initialization, stack entry and stack exit. Next, we use JavaScript prototype chain to implement.

Initialization queue

Initialize the data structure of a storage stack element if no empty array of default assignments is passed in.

function StackStudy(elements) {
    this.elements = elements || [];
}

Adding stack elements

Implement an enStack method to add elements to the stack. Note that only the stack head can be added, using the push method in the JavaScript array.

StackStudy.prototype.enStack = function(element) {
    this.elements.push(element);
}

Remove stack elements

Implement a deStack method that pops up elements at the end of the stack, using the pop method in the JavaScript array (which is different from the queue).

StackStudy.prototype.deStack = function() {
    return this.elements.pop();
}

Implementing it through JavaScript arrays is very simple. The source code is as follows:

https://github.com/Q-Angelo/project-training/tree/master/algorithm/stack-js.js

Classical application of stack

Through the previous explanation, I believe that the stack has a certain understanding, then what can it be used to do, this section cites several typical application cases.

Converting decimal system to binary, octal and hexadecimal system

Nowadays, decimal system is the most widely used expression in our life, and it is also the easiest to understand and remember. But when the computer is dealing with it, it must be converted to binary system for calculation. In the process of conversion between decimal system and binary system, octal system or hexadecimal system is usually used as abbreviation of binary system.

Therefore, this paper mainly explains the practical application of decimal, octal, hexadecimal and binary conversion in stack. First of all, you need to understand the rules of conversion between these data types, and it is not difficult to tell you through a graph.

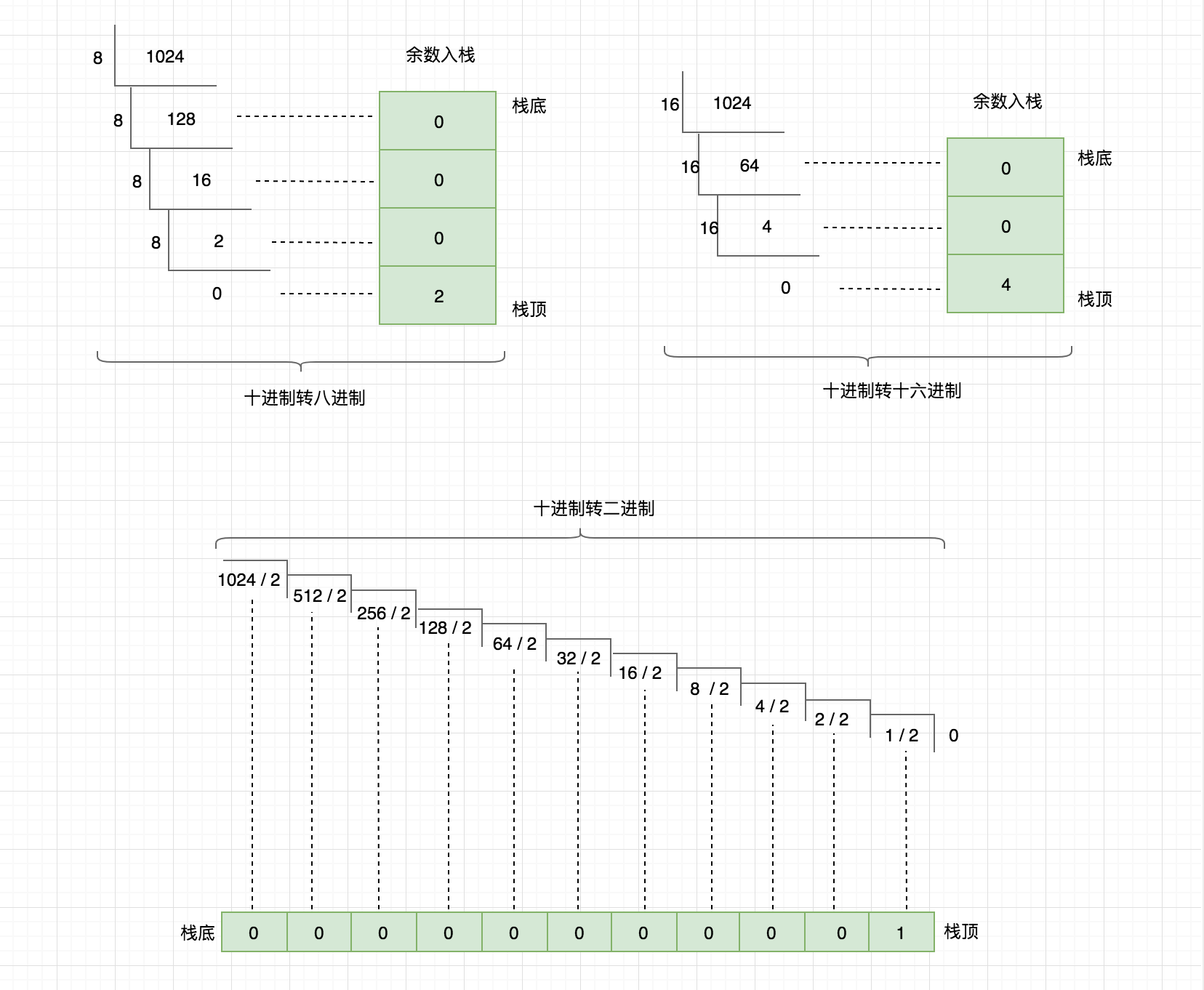
In the figure above, we divide the data types (binary, octal, hexadecimal) that need to be converted by decimal integer, and put the remainder into the stack. It's easy to understand that this principle is implemented in code.

Code

const StackStudy = require('./stack.js');
const str = '0123456789ABCDEF';

function dataConversion(num, type) {
    let x = num;
    const s1 = new StackStudy(20);

    while (x != 0) {
        s1.enStack(x % type);
        x = Math.floor(x / type);
    }

    while (!s1.isEmpty()) {
        console.log(str[s1.deStack()]);
    }

    console.log('--------------------');
    return;
}

Referring to the code we explained in the operation mechanism of the stack, we write the data Conversion method, and then traverse the stack and output it. The variable str defined in the code is used to deal with the occurrence of letters in hexadecimal system.

test

The following results are fully in line with our expectations, you can also use the computer's own calculator function to verify.

// Test octal
dataConversion(1024, 8); // 2000

// Test hexadecimal
dataConversion(1024, 16); // 400

// Testing hexadecimal with letters
dataConversion(3000, 16); // BB8

// Test binary
dataConversion(1024, 2); // 10000000000

Decimal to binary, octal, hexadecimal source address:

https://github.com/Q-Angelo/project-training/tree/master/algorithm/stack-data-conversion.js

Balanced parentheses

This is another practical problem. In some operations, you may have written the following expressions. In order to ensure the sequence of operations, parentheses are used, but it should be noted that the parentheses must be balanced. Each left parentheses should correspond to a right parentheses, otherwise the program will not work properly.

((1 + 2) * 3 * (4 + 5)) * 6

A balanced expression consisting of the above examples

(()())

Nonequilibrium expression

(()()

Realization steps of solving the problem of balanced parentheses by "stack"

• Initialize an empty stack {1}
• Traversing the symbol {2} to be detected
• What {3} symbols are needed for traversal
• If a character belongs to a stacked symbol ([{(...) it is stacked {3.1}
• If the character belongs to the closed symbol, the first step is to determine whether the stack space is empty and interrupt the operation if it is empty. Otherwise, the stack will go out. If the character of the stack is not the open symbol corresponding to the closed symbol, the detection fails and the interrupt operation jumps out of the loop {3.2}.
• Each cycle finishes to determine whether the current interruption occurs or not. If the operation has been interrupted, the illegal characters are stacked and the outermost character detection loop {4} is interrupted.
• Finally, it checks whether the stack is empty, if it is empty, it passes through, otherwise it does not pass through the output {5}.

Coding implementation

The following code can be understood by referring to the "Stack" implementation steps for solving the balanced parentheses problem

const Stack = require('./stack');
const detectionStr = '[]()'; // Define balanced symbols that need to be checked, and how to define other symbols in this format

function test(str) {
    let isTermination = false; // Whether to terminate, default false
    let stack = new Stack(20); // Initialization stack space {1}

    for (let i=0; i<str.length; i++) { // {2}
        const s = str[i];
        for (let d=0; d<detectionStr.length; d+=2) { // {3}
            const enStackStr = detectionStr[d]; // Stack character
            const deStackStr = detectionStr[d+1]; // Out-of-stack character

            switch (s) {
                case enStackStr : // Stack {3.1}
                    stack.enStack(s);
                    break;
                case deStackStr : // Out of Stack {3.2}
                    if (stack.isEmpty()) {
                        isTermination = true
                    } else {
                        const currElement = stack.deStack();
                        if (!currElement.includes(enStackStr)) { 
                            isTermination = true
                        }
                    }
                    break;
            }

            if (isTermination) break;
        }

        if (isTermination) { // Existence of mismatched symbols, early termination of {4}
            stack.enStack(s);
            break;
        }
    }

    if (stack.isEmpty()) { // {5}
        console.log('Testing pass');
    } else {
        console.log('Detection does not pass, detection does not pass symbols:');
        stack.traversing()
    }

    return stack.isEmpty();
}

Coding test

test('((()()[]])') // Detection does not pass, detection does not pass the symbol:](
test('()()[])') // Detection does not pass, detection does not pass symbols:)
test('[()()[]') // Detection does not pass, detection does not pass symbols:____________[
test('()()][]') // Testing pass

Balanced parentheses source address:

https://github.com/Q-Angelo/project-training/tree/master/algorithm/stack-balance-symbol.js