Red-black tree is one of many "balanced" search tree patterns, and in the worst case, its associated operation is O(log n).
1. Properties of red and black trees
A red-black tree is a binary lookup tree. Unlike ordinary binary lookup trees, each node of a red-black tree has a color attribute whose value is either red or black.
By restricting node colors on any simple path from root to leaf, the red-black tree ensures that there is no path twice as long as any other path, thus making the tree nearly balanced.
Assume that the attributes of a red-black tree node are key, color, left, right, and parent.
A red-black tree must satisfy the following characteristics (red-black tree characteristics):
- Each node in the tree is either red or black;
- The root node is black;
- Each leaf node (null) is black;
- If a node is red, both its children are black;
- There are the same number of black nodes for all paths from each node to any subsequent leaf node (null).
For the convenience of handling boundary conditions in the red-black tree code, we use a Sentry variable instead of null. For a red-black tree, the Sentry variable RedBlackTree.NULL (in the code below) is a node with the same attributes as other nodes, its color attribute is black, and other attributes can be arbitrarily valued.
We use the Sentry variable because we can treat a child node null of a node node as a normal node.
Here, we use the Sentry variable RedBlackTree.NULL instead of all nulls (the parent of all leaf and root nodes) in the tree.
We refer to the number of black nodes on the path from one node n (excluded) to any leaf node as the black height, expressed as bh(n). The black height of a red-black tree is the black height of its root node.
The codes for searching, minimizing, maximizing, precursor, and subsequent operations of the red-black tree are basically the same as those for the binary search tree. Binary Find Tree in java See.
The code below is given in conjunction with the above.
Color is represented by an enumeration class Color:
public enum Color {
Black("black"), Red("gules");
private String color;
private Color(String color) {
this.color = color;
}
@Override
public String toString() {
return color;
}
}
Class Node represents a node:
public class Node {
public int key;
public Color color;
public Node left;
public Node right;
public Node parent;
public Node() {
}
public Node(Color color) {
this.color = color;
}
public Node(int key) {
this.key = key;
this.color = Color.Red;
}
public int height() {
return Math.max(left != null ? left.height() : 0, right != null ? right.height() : 0) + 1;
}
public Node minimum() {
Node pointer = this;
while (pointer.left != RedBlackTree.NULL)
pointer = pointer.left;
return pointer;
}
@Override
public String toString() {
String position = "null";
if (this.parent != RedBlackTree.NULL)
position = this.parent.left == this ? "left" : "right";
return "[key: " + key + ", color: " + color + ", parent: " + parent.key + ", position: " + position + "]";
}
}
The class RedTreeNode represents a red-black tree:
public class RedBlackTree {
// Represents Sentry Variable
public final static Node NULL = new Node(Color.Black);
public Node root;
public RedBlackTree() {
this.root = NULL;
}
}
2. Rotation
The insertion and deletion of a red-black tree can change the structure of the tree, which may no longer have some of the characteristics mentioned above. To maintain these characteristics, we need to change the color and position of some nodes in the tree.
We can change the structure of the nodes by rotating. There are two main ways to rotate the nodes: left and right. This is shown in the following figure.
Left Rotation: Change the right child node of a node n to its parent node, and N to its left child node, so rightcannot be null. Then the right pointer of n is empty, and the left subtree of right is crowded out by n, so the original left subtree of right is called the right subtree of n.
Right Rotation: Change the left child of a node n left to its parent and N to the right child of left, so left cannot be null. Then the left pointer of n is empty and the right subtree of left is squeezed out by n, so the original right subtree of left is called the left subtree of n.
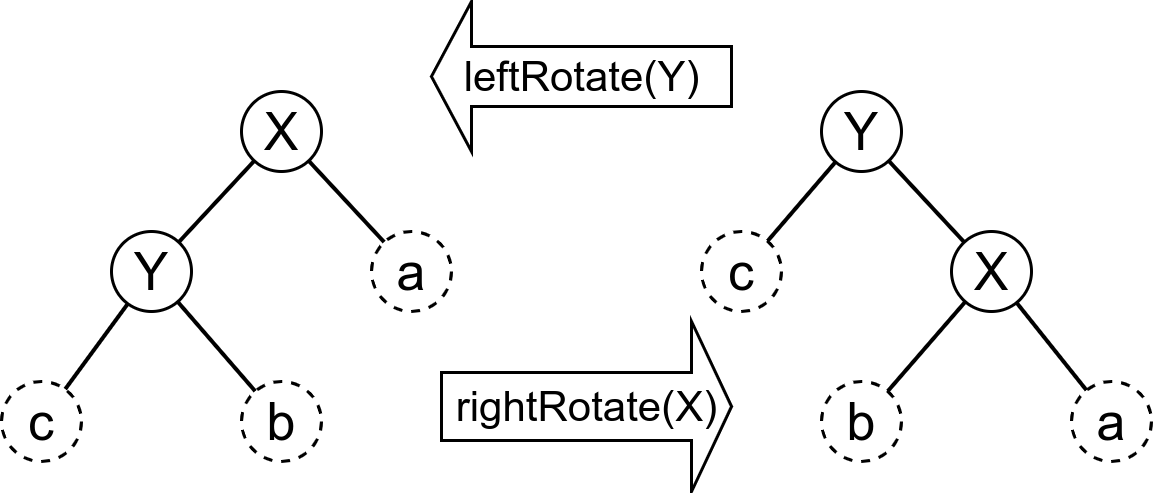
You can add the following implementation code to the RedTreeNode class:
public void leftRotate(Node node) {
Node rightNode = node.right;
node.right = rightNode.left;
if (rightNode.left != RedBlackTree.NULL)
rightNode.left.parent = node;
rightNode.parent = node.parent;
if (node.parent == RedBlackTree.NULL)
this.root = rightNode;
else if (node.parent.left == node)
node.parent.left = rightNode;
else
node.parent.right = rightNode;
rightNode.left = node;
node.parent = rightNode;
}
public void rightRotate(Node node) {
Node leftNode = node.left;
node.left = leftNode.right;
if (leftNode.right != RedBlackTree.NULL)
leftNode.right.parent = node;
leftNode.parent = node.parent;
if (node.parent == RedBlackTree.NULL) {
this.root = leftNode;
} else if (node.parent.left == node) {
node.parent.left = leftNode;
} else {
node.parent.right = leftNode;
}
leftNode.right = node;
node.parent = leftNode;
}
3. Insert
The insertion code of a red-black tree is very similar to that of a binary lookup tree. However, the insertion of a red-black tree changes the structure of the tree so that it does not have its own characteristics.
Here, the newly inserted node defaults to red.
So after inserting a node, you need code that maintains the red-black tree characteristics.
public void insert(Node node) {
Node parentPointer = RedBlackTree.NULL;
Node pointer = this.root;
while (this.root != RedBlackTree.NULL) {
parentPointer = pointer;
pointer = node.key < pointer.key ? pointer.left : pointer.right;
}
node.parent = parentPointer;
if(parentPointer == RedBlackTree.NULL) {
this.root = node;
}else if(node.key < parentPointer.key) {
parentPointer.left = node;
}else {
parentPointer.right = node;
}
node.left = RedBlackTree.NULL;
node.right = RedBlackTree.NULL;
node.color = Color.Red;
// Ways to maintain the properties of red and black trees
this.insertFixUp(node);
}
When inserting a new node using the above method, there are two kinds of situations that violate the characteristics of red and black trees.
- When there are no nodes in the tree, the inserted node is called the root node, and the color of this node is red.
- When a newly inserted node becomes a child of a red node, there is a red node with a red child node.
For the first case, you can set the root node to black directly; for the second case, you need to make corresponding solutions according to specific conditions.
The code is as follows:
public void insertFixUp(Node node) {
// When the node is not the root node and the parent node of the node is red
while (node.parent.color == Color.Red) {
// The solution varies depending on whether the node's parent is a left or right child node
if (node.parent == node.parent.parent.left) {
Node uncleNode = node.parent.parent.right;
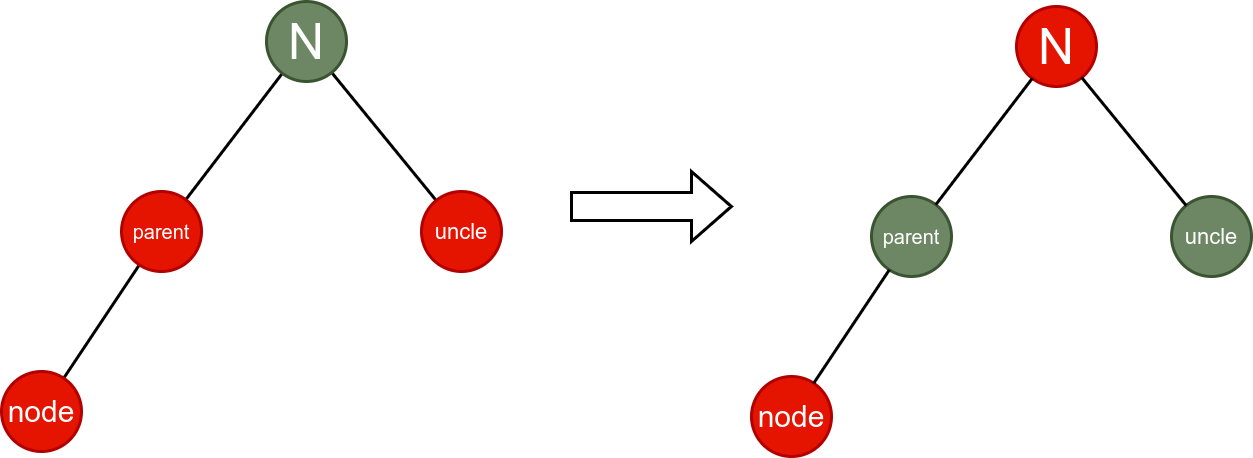
if (uncleNode.color == Color.Red) { // If uncle node is red, parent must be black
// By turning the parent and sibling nodes red, the parent and sibling nodes black, and then determining if the color of the parent and parent is appropriate
uncleNode.color = Color.Black;
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
node = node.parent.parent;
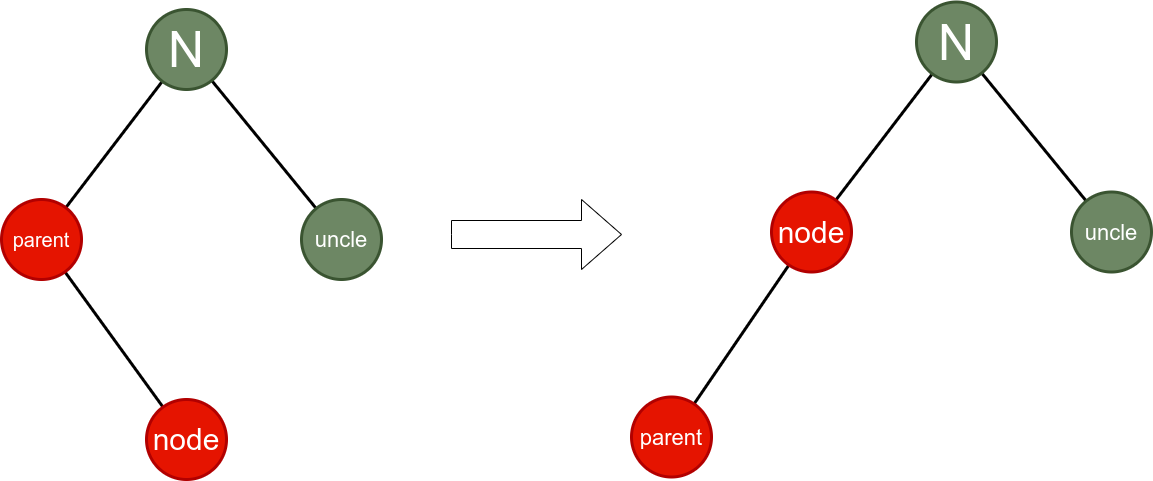
} else if (node == node.parent.right) {
node = node.parent;
this.leftRotate(node);
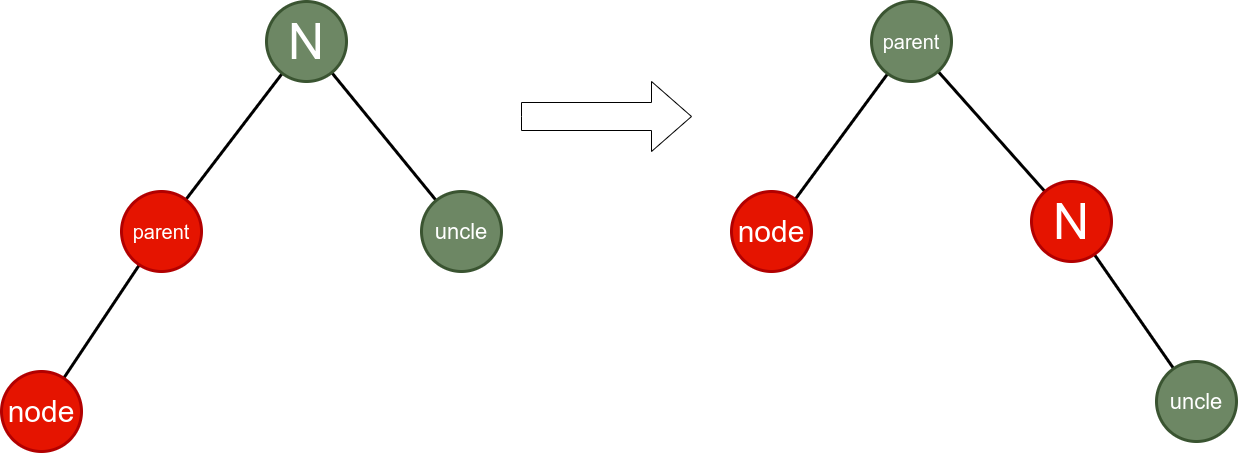
} else {
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
this.rightRotate(node.parent.parent);
}
} else {
Node uncleNode = node.parent.parent.left;
if (uncleNode.color == Color.Red) {
uncleNode.color = Color.Black;
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
node = node.parent.parent;
} else if (node == node.parent.left) {
node = node.parent;
this.rightRotate(node);
} else {
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
this.leftRotate(node.parent.parent);
}
}
}
// If there were no nodes in the previous tree, the newly added points would be new nodes, and the newly inserted nodes would be red, so they need to be modified.
this.root.color = Color.Black;
}
The following figure corresponds to the six cases in the second category and the corresponding processing results.
Situation 1:
Situation 2:
Situation 3:
Situation 4:
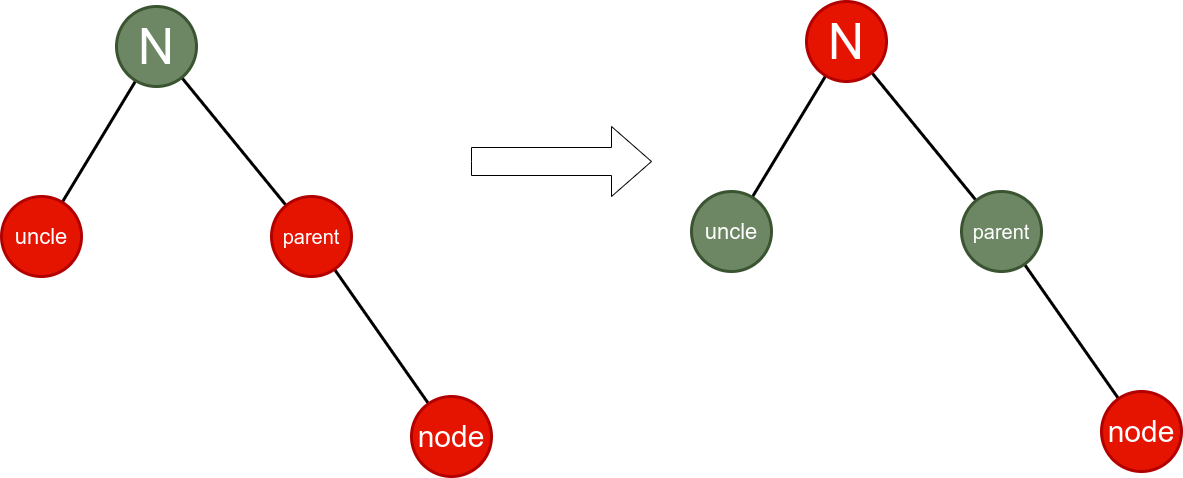
Situation 5:
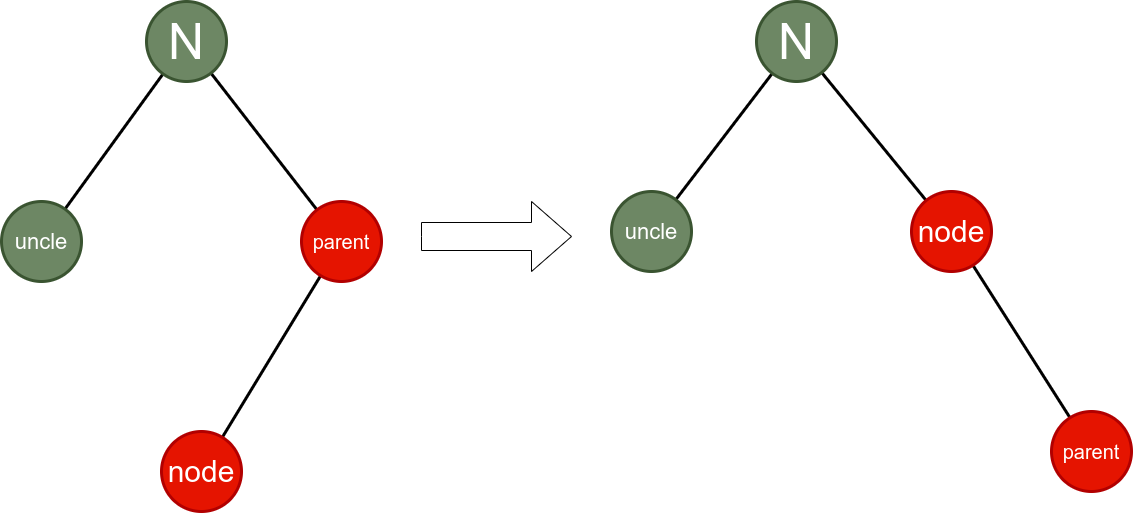
Situation 6:
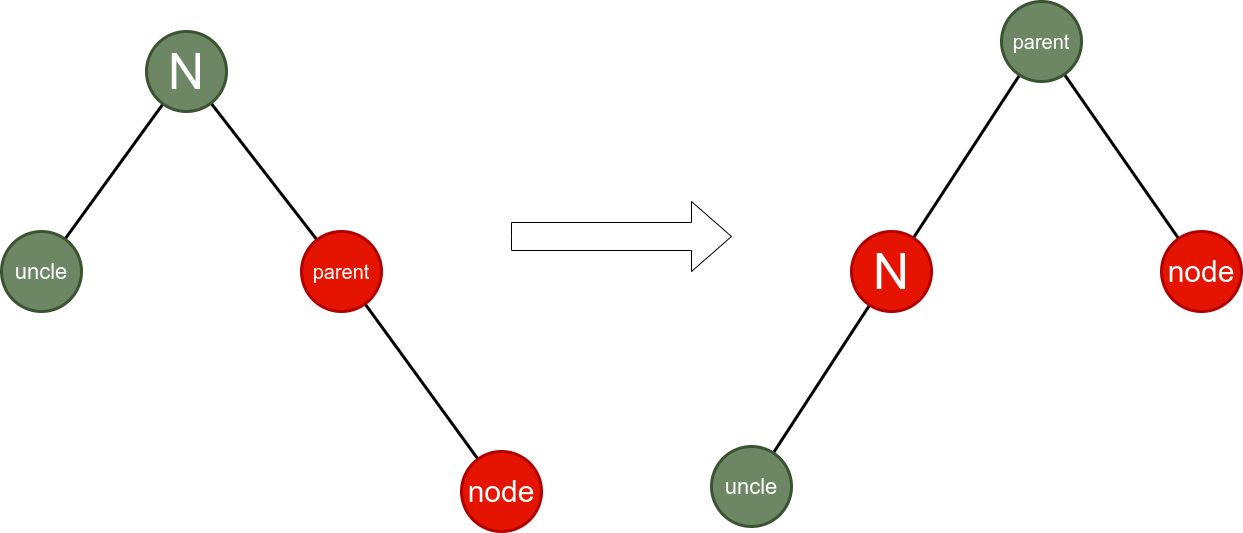
4. Delete
Deleting a node in a red-black tree replaces one node with another. So you need to implement this code first:
public void transplant(Node n1, Node n2) {
if(n1.parent == RedBlackTree.NULL){
this.root = n2;
}else if(n1.parent.left == n1) {
n1.parent.left = n2;
}else {
n1.parent.right = n2;
}
n2.parent = n1.parent;
}
The delete node code of the red-black tree is written based on the delete node code of the binary lookup tree.
Delete node code:
public void delete(Node node) {
Node pointer1 = node;
// Used to record deleted colors, regardless if they are red, but if they are black, they may destroy the properties of red-black trees
Color pointerOriginColor = pointer1.color;
// Used to record the point at which the problem occurred
Node pointer2;
if (node.left == RedBlackTree.NULL) {
pointer2 = node.right;
this.transplant(node, node.right);
} else if (node.right == RedBlackTree.NULL) {
pointer2 = node.left;
this.transplant(node, node.left);
} else {
// If the byte to be deleted has two child nodes, its immediate successor (right subtree minimum) is found, and the immediate successor node has no non-empty left child node.
pointer1 = node.right.minimum();
// Records the color of the immediate successor and its right child node
pointerOriginColor = pointer1.color;
pointer2 = pointer1.right;
// If it is directly followed by the right child node of the node, no processing is required
if (pointer1.parent == node) {
pointer2.parent = pointer1;
} else {
// Otherwise, extract the immediate successor from the tree to replace the node
this.transplant(pointer1, pointer1.right);
pointer1.right = node.right;
pointer1.right.parent = pointer1;
}
// Replace node with direct succession of node, inherit node color
this.transplant(node, pointer1);
pointer1.left = node.left;
pointer1.left.parent = pointer1;
pointer1.color = node.color;
}
if (pointerOriginColor == Color.Black) {
this.deleteFixUp(pointer2);
}
}
When the color of the deleted node is black, a method needs to be called to maintain the red-black tree's characteristics.
There are two main types of situations:
- When the node is red, it turns black directly.
- When the node is black, the red-black tree structure needs to be adjusted.
private void deleteFixUp(Node node) {
// If the node is not the root node and is black
while (node != this.root && node.color == Color.Black) {
// If a node is the left child of its parent
if (node == node.parent.left) {
// Record node's sibling nodes
Node pointer1 = node.parent.right;
// If his brother node is red
if (pointer1.color == Color.Red) {
pointer1.color = Color.Black;
node.parent.color = Color.Red;
leftRotate(node.parent);
pointer1 = node.parent.right;
}
if (pointer1.left.color == Color.Black && pointer1.right.color == Color.Black) {
pointer1.color = Color.Red;
node = node.parent;
} else if (pointer1.right.color == Color.Black) {
pointer1.left.color = Color.Black;
pointer1.color = Color.Red;
rightRotate(pointer1);
pointer1 = node.parent.right;
} else {
pointer1.color = node.parent.color;
node.parent.color = Color.Black;
pointer1.right.color = Color.Black;
leftRotate(node.parent);
node = this.root;
}
} else {
// Record node's sibling nodes
Node pointer1 = node.parent.left;
// If his brother node is red
if (pointer1.color == Color.Red) {
pointer1.color = Color.Black;
node.parent.color = Color.Red;
rightRotate(node.parent);
pointer1 = node.parent.left;
}
if (pointer1.right.color == Color.Black && pointer1.left.color == Color.Black) {
pointer1.color = Color.Red;
node = node.parent;
} else if (pointer1.left.color == Color.Black) {
pointer1.right.color = Color.Black;
pointer1.color = Color.Red;
leftRotate(pointer1);
pointer1 = node.parent.left;
} else {
pointer1.color = node.parent.color;
node.parent.color = Color.Black;
pointer1.left.color = Color.Black;
rightRotate(node.parent);
node = this.root;
}
}
}
node.color = Color.Black;
}
For the second case, there are eight types:
Situation 1:
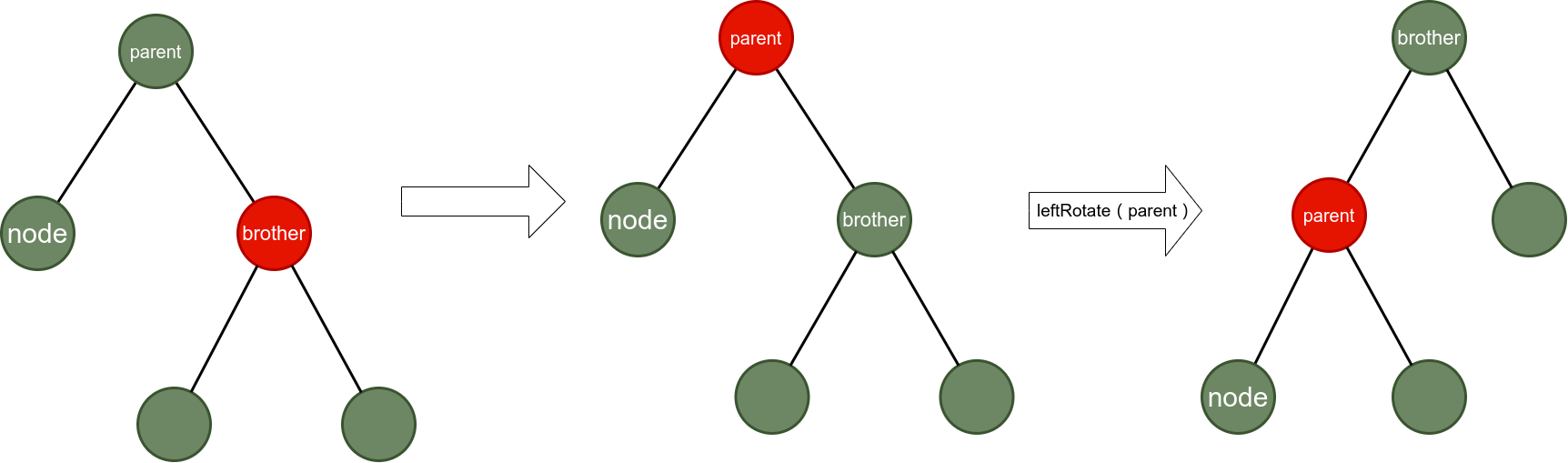
Situation 2:
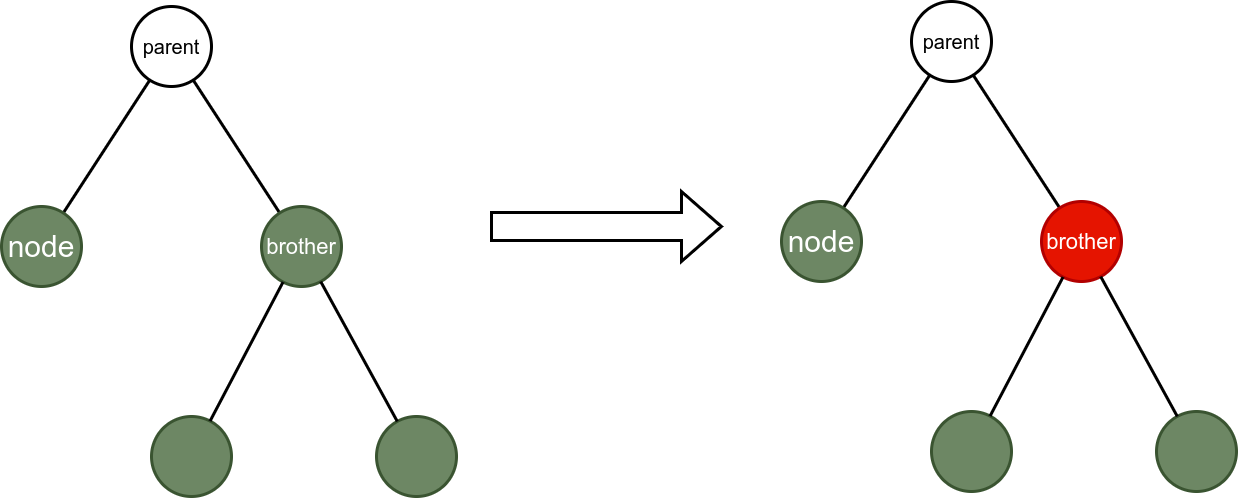
Situation 3:
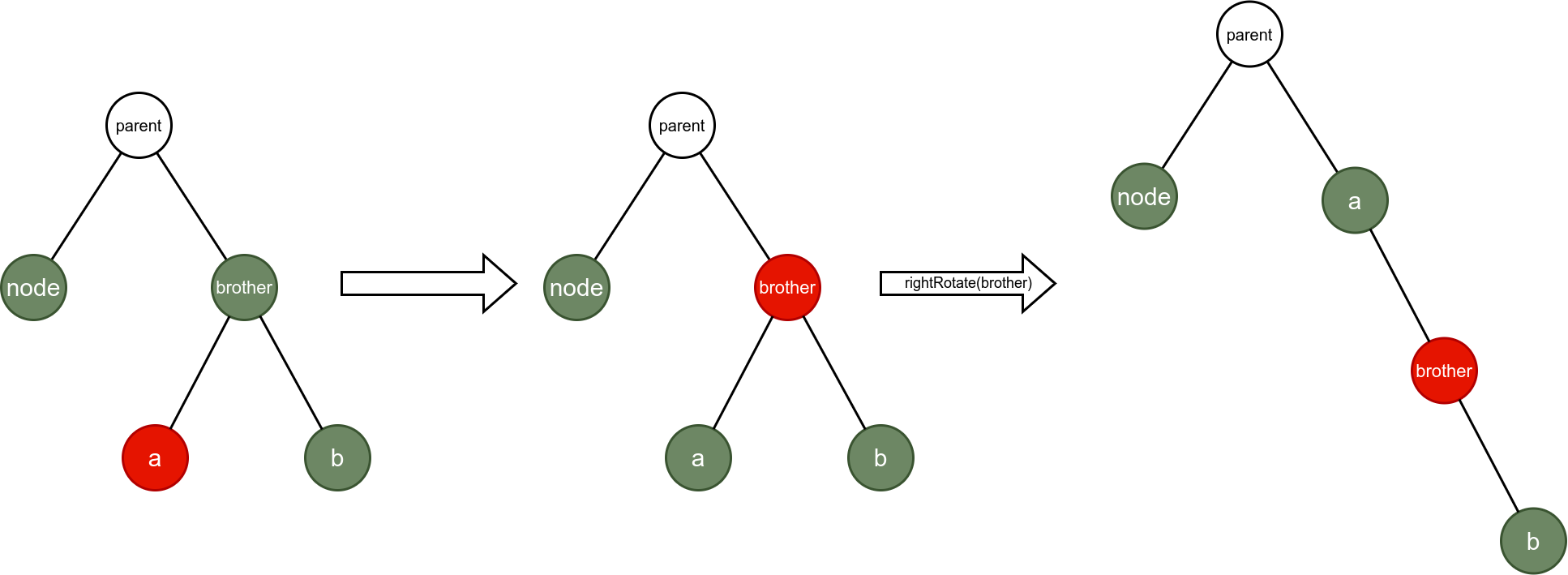
Situation 4:
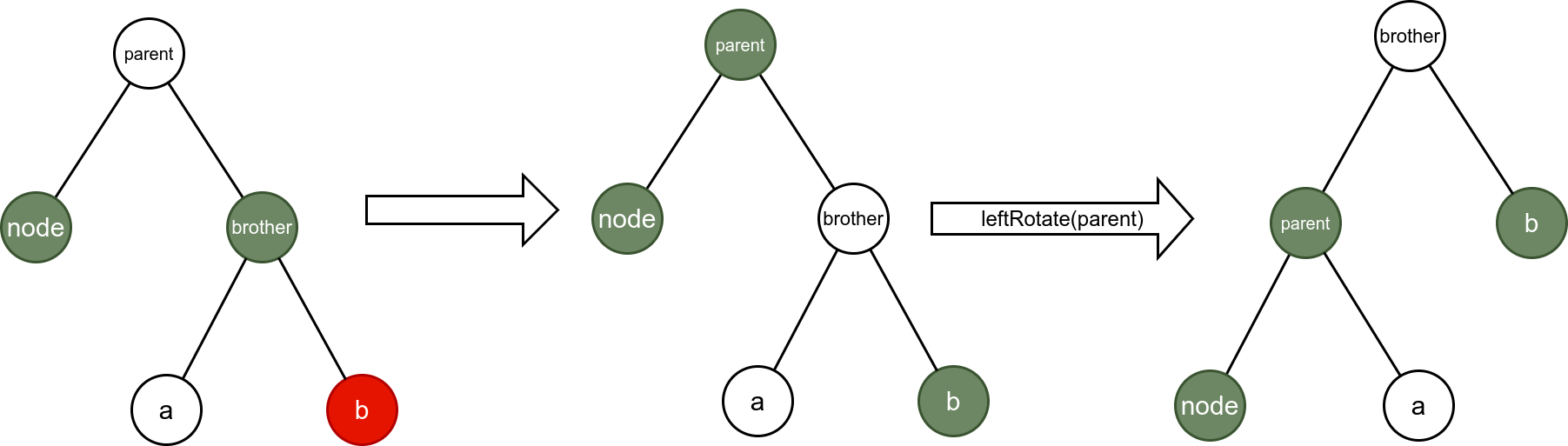
Situation 5:
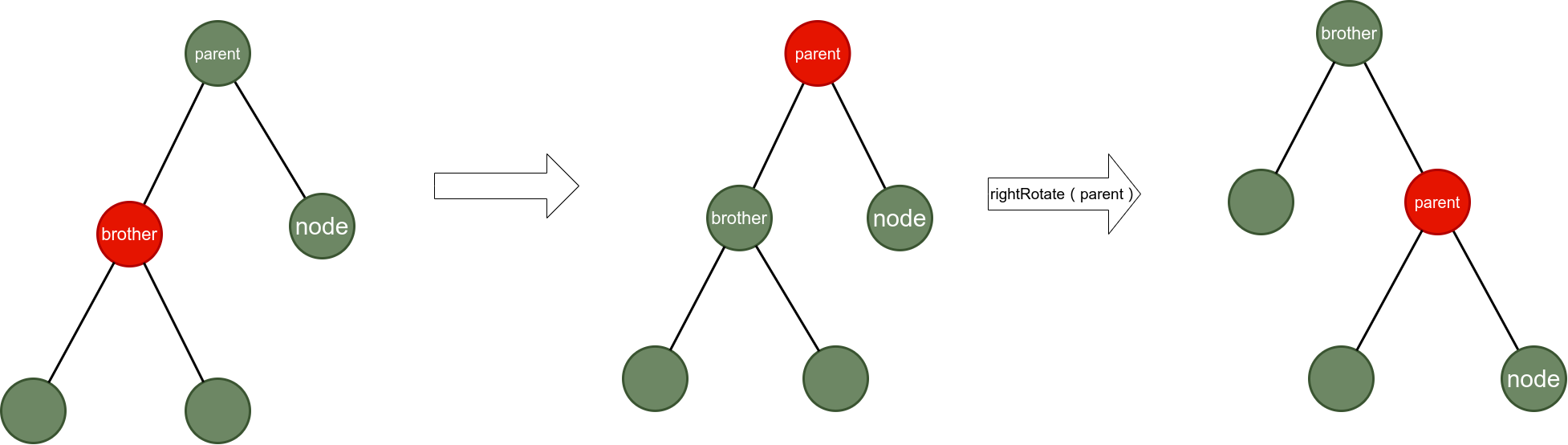
Situation 6:
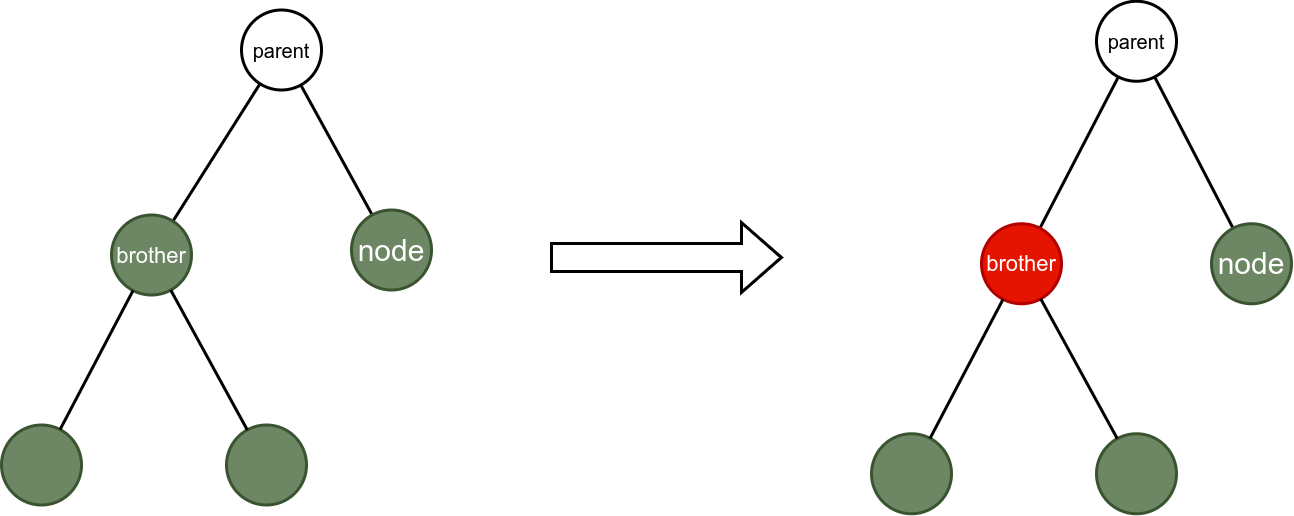
Situation 7:
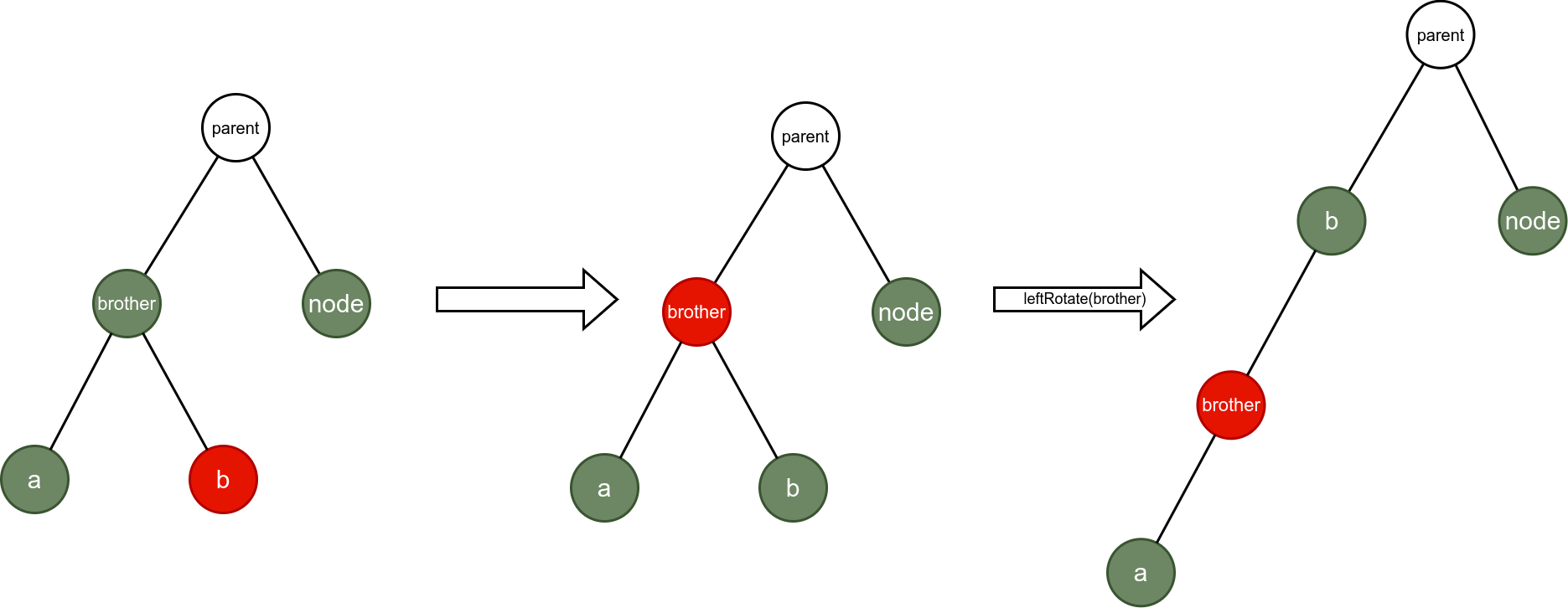
Situation 8:
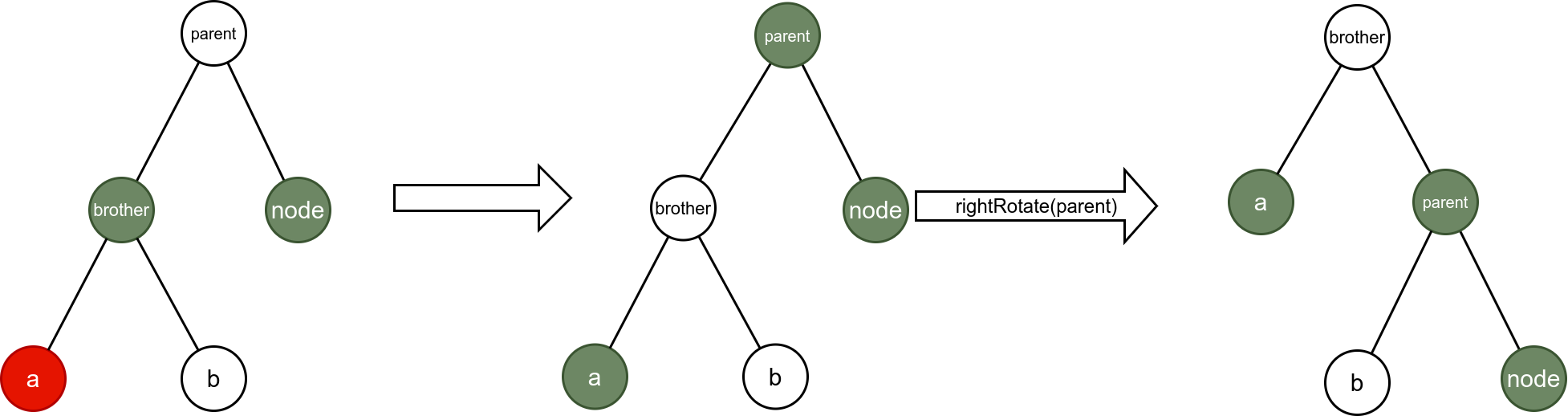
5. All Codes
public enum Color {
Black("black"), Red("gules");
private String color;
private Color(String color) {
this.color = color;
}
@Override
public String toString() {
return color;
}
}
public class Node {
public int key;
public Color color;
public Node left;
public Node right;
public Node parent;
public Node() {
}
public Node(Color color) {
this.color = color;
}
public Node(int key) {
this.key = key;
this.color = Color.Red;
}
/**
* Find the height of a node in a tree species
*
* @return
*/
public int height() {
return Math.max(left != null ? left.height() : 0, right != null ? right.height() : 0) + 1;
}
/**
* Find the smallest node in the tree with this node as the root node
*
* @return
*/
public Node minimum() {
Node pointer = this;
while (pointer.left != RedBlackTree.NULL)
pointer = pointer.left;
return pointer;
}
@Override
public String toString() {
String position = "null";
if (this.parent != RedBlackTree.NULL)
position = this.parent.left == this ? "left" : "right";
return "[key: " + key + ", color: " + color + ", parent: " + parent.key + ", position: " + position + "]";
}
}
import java.util.LinkedList;
import java.util.Queue;
public class RedBlackTree {
public final static Node NULL = new Node(Color.Black);
public Node root;
public RedBlackTree() {
this.root = NULL;
}
/**
* Left Rotation
*
* @param node
*/
public void leftRotate(Node node) {
Node rightNode = node.right;
node.right = rightNode.left;
if (rightNode.left != RedBlackTree.NULL)
rightNode.left.parent = node;
rightNode.parent = node.parent;
if (node.parent == RedBlackTree.NULL)
this.root = rightNode;
else if (node.parent.left == node)
node.parent.left = rightNode;
else
node.parent.right = rightNode;
rightNode.left = node;
node.parent = rightNode;
}
/**
* Right Rotation
*
* @param node
*/
public void rightRotate(Node node) {
Node leftNode = node.left;
node.left = leftNode.right;
if (leftNode.right != RedBlackTree.NULL)
leftNode.right.parent = node;
leftNode.parent = node.parent;
if (node.parent == RedBlackTree.NULL) {
this.root = leftNode;
} else if (node.parent.left == node) {
node.parent.left = leftNode;
} else {
node.parent.right = leftNode;
}
leftNode.right = node;
node.parent = leftNode;
}
public void insert(Node node) {
Node parentPointer = RedBlackTree.NULL;
Node pointer = this.root;
while (pointer != RedBlackTree.NULL) {
parentPointer = pointer;
pointer = node.key < pointer.key ? pointer.left : pointer.right;
}
node.parent = parentPointer;
if (parentPointer == RedBlackTree.NULL) {
this.root = node;
} else if (node.key < parentPointer.key) {
parentPointer.left = node;
} else {
parentPointer.right = node;
}
node.left = RedBlackTree.NULL;
node.right = RedBlackTree.NULL;
node.color = Color.Red;
this.insertFixUp(node);
}
private void insertFixUp(Node node) {
// When the node is not the root node and the parent node of the node is red
while (node.parent.color == Color.Red) {
// The solution varies depending on whether the node's parent is a left or right child node
if (node.parent == node.parent.parent.left) {
Node uncleNode = node.parent.parent.right;
if (uncleNode.color == Color.Red) { // If uncle node is red, parent must be black
// By turning the parent and sibling nodes red, the parent and sibling nodes black, and then determining if the color of the parent and parent is appropriate
uncleNode.color = Color.Black;
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
node = node.parent.parent;
} else if (node == node.parent.right) { // Node is the right child of its parent node and uncle node is black
// Rotate the parent node of a node left
node = node.parent;
this.leftRotate(node);
} else { // Node If uncle node is black, node is the left child of its parent node, and parent node is black
// Make the parent black, the parent red, rotate the parent right
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
this.rightRotate(node.parent.parent);
}
} else {
Node uncleNode = node.parent.parent.left;
if (uncleNode.color == Color.Red) {
uncleNode.color = Color.Black;
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
node = node.parent.parent;
} else if (node == node.parent.left) {
node = node.parent;
this.rightRotate(node);
} else {
node.parent.color = Color.Black;
node.parent.parent.color = Color.Red;
this.leftRotate(node.parent.parent);
}
}
}
// If there were no nodes in the previous tree, the newly added points would be new nodes, and the newly inserted nodes would be red, so they need to be modified.
this.root.color = Color.Black;
}
/**
* n2 Replace n1
*
* @param n1
* @param n2
*/
private void transplant(Node n1, Node n2) {
if (n1.parent == RedBlackTree.NULL) { // If n1 is the root node
this.root = n2;
} else if (n1.parent.left == n1) { // If n1 is the left child of its parent
n1.parent.left = n2;
} else { // If n1 is the right child of its parent
n1.parent.right = n2;
}
n2.parent = n1.parent;
}
/**
* Delete node
*
* @param node
*/
public void delete(Node node) {
Node pointer1 = node;
// Used to record deleted colors, regardless if they are red, but if they are black, they may destroy the properties of red-black trees
Color pointerOriginColor = pointer1.color;
// Used to record the point at which the problem occurred
Node pointer2;
if (node.left == RedBlackTree.NULL) {
pointer2 = node.right;
this.transplant(node, node.right);
} else if (node.right == RedBlackTree.NULL) {
pointer2 = node.left;
this.transplant(node, node.left);
} else {
// If the byte to be deleted has two child nodes, its immediate successor (right subtree minimum) is found, and the immediate successor node has no non-empty left child node.
pointer1 = node.right.minimum();
// Records the color of the immediate successor and its right child node
pointerOriginColor = pointer1.color;
pointer2 = pointer1.right;
// If it is directly followed by the right child node of the node, no processing is required
if (pointer1.parent == node) {
pointer2.parent = pointer1;
} else {
// Otherwise, extract the immediate successor from the tree to replace the node
this.transplant(pointer1, pointer1.right);
pointer1.right = node.right;
pointer1.right.parent = pointer1;
}
// Replace node with direct succession of node, inherit node color
this.transplant(node, pointer1);
pointer1.left = node.left;
pointer1.left.parent = pointer1;
pointer1.color = node.color;
}
if (pointerOriginColor == Color.Black) {
this.deleteFixUp(pointer2);
}
}
/**
* The procedure RB-DELETE-FIXUP restores properties 1, 2, and 4
*
* @param node
*/
private void deleteFixUp(Node node) {
// If the node is not the root node and is black
while (node != this.root && node.color == Color.Black) {
// If a node is the left child of its parent
if (node == node.parent.left) {
// Record node's sibling nodes
Node pointer1 = node.parent.right;
// If the node sibling node is red
if (pointer1.color == Color.Red) {
pointer1.color = Color.Black;
node.parent.color = Color.Red;
leftRotate(node.parent);
pointer1 = node.parent.right;
}
if (pointer1.left.color == Color.Black && pointer1.right.color == Color.Black) {
pointer1.color = Color.Red;
node = node.parent;
} else if (pointer1.right.color == Color.Black) {
pointer1.left.color = Color.Black;
pointer1.color = Color.Red;
rightRotate(pointer1);
pointer1 = node.parent.right;
} else {
pointer1.color = node.parent.color;
node.parent.color = Color.Black;
pointer1.right.color = Color.Black;
leftRotate(node.parent);
node = this.root;
}
} else {
// Record node's sibling nodes
Node pointer1 = node.parent.left;
// If his brother node is red
if (pointer1.color == Color.Red) {
pointer1.color = Color.Black;
node.parent.color = Color.Red;
rightRotate(node.parent);
pointer1 = node.parent.left;
}
if (pointer1.right.color == Color.Black && pointer1.left.color == Color.Black) {
pointer1.color = Color.Red;
node = node.parent;
} else if (pointer1.left.color == Color.Black) {
pointer1.right.color = Color.Black;
pointer1.color = Color.Red;
leftRotate(pointer1);
pointer1 = node.parent.left;
} else {
pointer1.color = node.parent.color;
node.parent.color = Color.Black;
pointer1.left.color = Color.Black;
rightRotate(node.parent);
node = this.root;
}
}
}
node.color = Color.Black;
}
private void innerWalk(Node node) {
if (node != NULL) {
innerWalk(node.left);
System.out.println(node);
innerWalk(node.right);
}
}
/**
* Intermediate traversal
*/
public void innerWalk() {
this.innerWalk(this.root);
}
/**
* level traversal
*/
public void print() {
Queue<Node> queue = new LinkedList<>();
queue.add(this.root);
while (!queue.isEmpty()) {
Node temp = queue.poll();
System.out.println(temp);
if (temp.left != NULL)
queue.add(temp.left);
if (temp.right != NULL)
queue.add(temp.right);
}
}
// lookup
public Node search(int key) {
Node pointer = this.root;
while (pointer != NULL && pointer.key != key) {
pointer = pointer.key < key ? pointer.right : pointer.left;
}
return pointer;
}
}
6. Demonstration
Demo code:
public class Test01 {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8 };
RedBlackTree redBlackTree = new RedBlackTree();
for (int i = 0; i < arr.length; i++) {
redBlackTree.insert(new Node(arr[i]));
}
System.out.println("Tree height: " + redBlackTree.root.height());
System.out.println("Left subtree height: " + redBlackTree.root.left.height());
System.out.println("Height of right subtree: " + redBlackTree.root.right.height());
System.out.println("level traversal");
redBlackTree.print();
// To delete a node
Node node = redBlackTree.search(4);
redBlackTree.delete(node);
System.out.println("Tree height: " + redBlackTree.root.height());
System.out.println("Left subtree height: " + redBlackTree.root.left.height());
System.out.println("Height of right subtree: " + redBlackTree.root.right.height());
System.out.println("level traversal");
redBlackTree.print();
}
}
Result:
Tree height: 5 Left subtree height: 3 Height of right subtree: 4 level traversal [key: 4, color: black, parent: 0, position: null] [key: 2, color: gules, parent: 4, position: left] [key: 6, color: gules, parent: 4, position: right] [key: 1, color: black, parent: 2, position: left] [key: 3, color: black, parent: 2, position: right] [key: 5, color: black, parent: 6, position: left] [key: 7, color: black, parent: 6, position: right] [key: 8, color: gules, parent: 7, position: right] Tree height: 4 Left subtree height: 3 Height of right subtree: 3 level traversal [key: 5, color: black, parent: 0, position: null] [key: 2, color: gules, parent: 5, position: left] [key: 7, color: gules, parent: 5, position: right] [key: 1, color: black, parent: 2, position: left] [key: 3, color: black, parent: 2, position: right] [key: 6, color: black, parent: 7, position: left] [key: 8, color: black, parent: 7, position: right]
7. Reference
Introduction to Algorithms (3rd Edition) English version