The simplest version: only one trading opportunity, buy and sell one day: buy and sell stocks 1

//For each day i, as long as you know which day is the smallest in front, you can know the maximum profit ending with i
    int maxProfit(vector<int>& prices) {
        int buyDay = 0;
        int maxProfit = 0;
        for(int i=1;i<prices.size();i++){
            if(prices[i]<prices[buyDay])
                buyDay = i;
            int tempProfit = prices[i] - prices[buyDay];
            maxProfit = max(maxProfit,tempProfit);
        }
        return maxProfit;
    }

Unlimited Trading: buying and selling stocks 2

You can complete as many transactions as possible (buying and selling a stock multiple times)

 //Continuous holding can also be regarded as buying and selling. Anyway, the number of times is unlimited
    int maxProfit(vector<int>& prices) {
        int profitSum = 0;
        for(int i=1;i<prices.size();i++){
            if(prices[i] < prices[i-1] ){
                continue;
            }
            profitSum += prices[i] - prices[i-1]; //Buy and sell as long as there is profit
        }
        return profitSum;
    }

The second writing method, general solution, state transition.

//dp[i][1] holds shares on day I, and dp[i][0] does not hold shares on day I
    int maxProfit(vector<int>& prices) {
        int dp[100005][2];
        dp[0][0] = 0; 
        dp[0][1] = -prices[0];  //If you buy initially, the profit until day 0 is negative
        for(int i=1;i<prices.size();i++){
        
            dp[i][0] = max(dp[i-1][1] + prices[i], dp[i-1][0]); //Not held = not held the previous day or held the previous day + sold today
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]); //Holding = holding the previous day or not holding the previous day + buying today

        }
        return dp[prices.size()-1][0];  
    }

Including freezing period

My original idea was that according to the above 2, I only need to judge the time of buying d p [ i ] = d p [ i − 1 ] [ 0 ] − p r i c e dp[i]=dp[i-1][0] - price dp[i]=dp[i − 1] [0] − price whether i-1 was sold the day before, the judgment logic is to see whether dp[i-2][0] is the same as [i-1]. However, the reason for this is that the freezing period will have an impact on the later. Therefore, it is impossible to simply confirm the optimal value of dp[i][0] in day I. you seem to be the best at present, but your freezing pair may delay the later big list. Therefore, the freezing period should also be part of the state.

If [0] is not held

• Sell today - it will affect the next day
• Sell yesterday, or sell before, postpone before - it has no impact on the future

In order to distinguish, let's sell today or [0], and record those not sold today as [2]

Sort out the state transition:
dp[i][1] = dp[i-1][1] o r or or dp[i-1][2] - price
dp[i][0] = dp[i-1][1] + price
dp[i][2] = dp[i-1][0] o r or or dp[i-1][2]

int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int> > dp(n,vector<int>(3,0)); //0 means to sell today (no buying later), 1 means to hold now, and 2 means to sell yesterday and before
        dp[0][1] = -prices[0];

        for(int i=1; i<n; i++){
            dp[i][0] = dp[i-1][1] + prices[i];
            dp[i][1] = max(dp[i-1][1],dp[i-1][2]-prices[i]);
            dp[i][2] = max(dp[i-1][0],dp[i-1][2]);
        }
        return max(dp[n-1][0],dp[n-1][2]);
    }

We found that this type of question is not difficult to think about the state transition. The important thing is to analyze several states.

General solution to the stock problem: give you the daily price of the stock, limit you to only buy and sell K times, and seek the maximum income.

In order to obtain the income of K transactions on the nth day, the usual idea of dynamic planning is: dp[n][k]
Therefore, we can think of using dp[i][j] to represent the profit of j transactions up to day I.

There are only three choices for us to think about every day: sell, buy and keep
Because sell and buy have a preorder relationship, we must have buy in front of them to sell. Therefore, our state must add one dimension to indicate whether we have bought in front.

• dp[][][0] means no buy
• dp[][][1] indicates that it has been bought

state transition
(buy indicates entering the next transaction j+1)

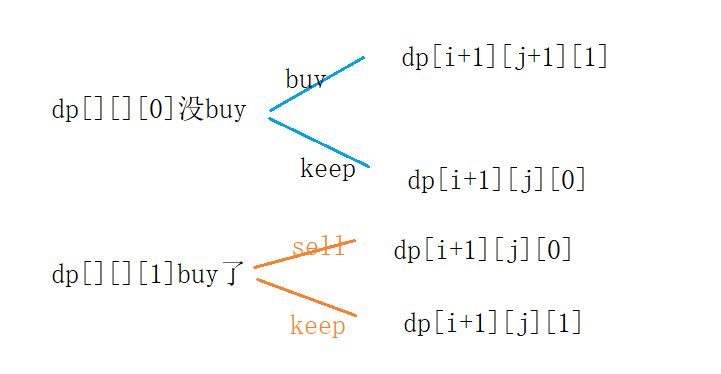
From this, we deduce our formula: the value of dp represents profit

d p [ i ] [ j ] [ 0 ] = m a x ( d p [ i − 1 ] [ j ] [ 0 ] , d p [ i − 1 ] [ j ] [ 1 ] + p r i c e s [ i ] ) dp[i][j][0] = max( dp[i-1][j][0], dp[i-1][j][1] + prices[i]) dp[i][j][0]=max(dp[i−1][j][0],dp[i−1][j][1]+prices[i])

d p [ i ] [ j ] [ 1 ] = m a x ( d p [ i − 1 ] [ j ] [ 1 ] , d p [ i − 1 ] [ j − 1 ] [ 0 ] − p r i c e s [ i ] ) dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]) dp[i][j][1]=max(dp[i−1][j][1],dp[i−1][j−1][0]−prices[i])

Note the initial state, that is, when i-1 may not exist and j-1 may not exist in the transition.
i == 0: dp[0][][1] = -prices[i] / / indicates initial purchase
j == 0: dp[][0][1] = -inf / / indicates impossible

 int maxProfit(vector<int>& prices) {
        int dp[100005][3][2] = {0};
        int inf = 1000000000;
    
        for(int i=0;i<prices.size();i++){
            for(int k=0;k<=2;k++){                   
                //In the middle, I-1 and k-1 do not exist
                if( k==0 ){
                    dp[i][k][1] = -inf;
                    continue;
                }
                if(i==0){
                    dp[i][k][1] = -prices[i]; 
                    continue;
                }
                dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+prices[i]);
                dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i]);
            }
        }
        return dp[prices.size()-1][2][0];
    }