preface

Graph theory has always been my biggest headache - 2021 / 9 / 4

Now I finally don't have a headache

After grinding on dijkstra for a day, I finally realized him completely

On graph theory

Graph theory has always been the final topic in the competition, and it is also a difficult point
In the popularity group, graph theory is generally the storage and shortest path

The first graph we contact should be a tree. The tree is a kind of graph. Its extended bfs is also the shortest path: the shortest path without edge weight, so graph theory is broad and profound

On path relaxation

For example, the distance from Xiaoming to Xiaogang's house is 100m, that from Xiaogang to Xiaohong's house is 50m, and that from Xiaoming to Xiaohong's house is 300m. How many meters is the shortest distance from Xiaoming to Xiaohong's house?

It's very simple. It takes 150 meters to transfer from Xiaogang's house to Xiaohong's house,
This is relaxation. On the basis of the original long journey, "detour" makes the journey shorter

Storage of drawings

adjacency matrix

Advantages: easy to understand
Disadvantages: space and time are very limited

Thought and demonstration

Adjacency matrix is the simplest storage method
To save a graph is to save the relationship between vertices
The adjacency matrix is like the following table:

\	v1	v2	v3
v1	0	∞	∞
v2	∞	0	∞
v3	∞	∞	0

(I also studied Markdown for this form)
As indicated, the adjacency matrix is based on a two-dimensional array to express the relationship between v1, v2 and v3 edges. If there is a connection, there will be a value. If there is no connection, there will be no value.

Code implementation adjacency matrix storage

#include <iostream>
#define INF 0x3f3f3f3f 	// Inf refers to infinity, in the range of int 
using namespace std;
const int N=1e3;	//Because of the space problem, the adjacency matrix can only be stored to 1000 
int n,m;	//n vertices, m edges
int arcs[N][N]; 
int main(){
	cin>>n>>m;
	cin>>u>>v>>w;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			arcs[i][j]=INF; 
		}
	}
	for(int i=1;i<=m;i++){	//Input of m vertices 
		cin>>u>>v>>w;
		arcs[u][v]=w;
		arcs[v][u]=w;
	}
}

On the shortest path of adjacency matrix (Floyd)

Can adjacency matrix be the shortest path
Adjacency matrix has a special shortest path algorithm: Floyd
Floyd relaxes the edges based on the adjacency matrix

With concrete implementation, we can imitate the above relaxation
Pseudo code:
v1->v2=min(v1->v2,v1->v3+v3->v2);
That's about it
How should the code be implemented

Code implementation Floyd shortest path

#include <iostream>
#define INF 0x3f3f3f3f 	// Inf refers to infinity, in the range of int 
using namespace std;
const int N=1e3;	//Because of the space problem, the adjacency matrix can only be stored to 1000 
int n,m;	//n vertices, m edges
int arcs[N][N]; 
int main(){
	cin>>n>>m;
	cin>>u>>v>>w;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			arcs[i][j]=INF; 
		}
	}
	for(int i=1;i<=m;i++){	//Input of m vertices 
		cin>>u>>v>>w;
		arcs[u][v]=w;
		arcs[v][u]=w;
	}
	
	//Relaxed edge 
	for(int k=1;k<=n;k++){	//Xiao Gang's house 
		for(int i=1;i<=n;i++){	//Xiaoming family 
			for(int j=1;j<=n;j++){	//Xiaohong family 
				int w1=acrs[i][j];	//Xiao Ming goes directly to Xiao Hong's house
				int w2=acrs[i][k]+arcs[k][j];	//Xiaoming went to Xiaohong's house from Xiaogang's house 
				acrs[i][j]=min(acrs[i][j],acrs[i][k]+acrs[k][j]);	//See which way is closer 
			}
		}
	}
}

Adjacency table

Advantages: space saving
Disadvantages: vector is nlongn (basically negligible)

Thought and demonstration

The previous adjacency matrix wastes a lot of space. Some points are not connected at all, but they will be expressed on the adjacency matrix, which is very wasteful. How to optimize it

Can we say that the v1 array stores the vertices and distances connected to it

Adjacency table is to improve adjacency matrix and waste space, so in order to save space as much as possible, we can use vector array

But the array can only store one number

So we can use struct to represent the number connected to it and the corresponding distance
That is, a structure vector array

Code implementation adjacency table storage diagram

#include <iostream>
#include <vector>
using namespace std;
const int N=1e4+10;
int n,m;	//n vertices, m edges 
struct node {	
	int to,w;	//Next vertex and distance 
};
vector<node>edge[N];	//vector array storage relationship 

void add(int u,int v,int w) {	//Connecting two vertices u, v, the distance is w 
	edge[u].push_back({v,w});
//	edge[v].push_back({u,w}); 	//  If it's an undirected graph, add this paragraph 
}

int main() {
	cin>>n>>m;
	int u,v,w;	//There is a path from point u to point v, and the path length is w 
	for(int i=1;i<=m;i++){
		cin>>u>>v>>w;
		add(u,v,w);	//connect 
	}
	return 0;
}

On the shortest path of adjacency table (dijkstra)

This algorithm is nicknamed DJ Godzilla by our community
It's also one of the nightmares

The Floyd algorithm above has the shortest path, and the time complexity is n^ 3. The time complexity of dijkstra is n^ 2 and nlogn, so it is much more efficient than Floyd. Of course, efficient is also a more complex implementation,

Let's continue to follow Floyd's thought, or relax on the original basis

This relaxation is interesting. It is an edge relaxation. If you relax, this edge will have a fixed value. It's very vague. I'll borrow a picture from other bloggers

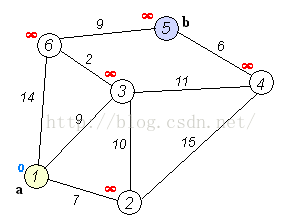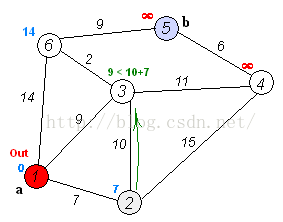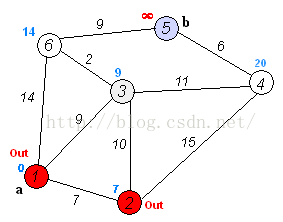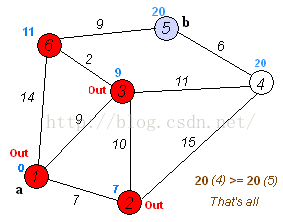
This picture comes from chart

This picture is the clearest one I have found

Each time, the program will select the point with the shortest distance from the starting point, relax the point connected with it, and then determine the value of this point (that is, the red in the figure). After determining each point, it will end

The code implements the shortest path of the lead table (dijkstra) (n^2)

#include <iostream>
#include <vector>
#include <cstring>
#include <string>
#define INF 0x3f3f3f3f 	// Represents infinity 
using namespace std;
const int N=1e4+10;
int n,m;	//There are n vertices and m edges 
struct node {
	int to,w;	//The next point and distance connected to him 
};
bool vs[N];	//Whether the vs judgment point has been determined
int d[N];	//The current distance from each point to the starting point	 
vector<node>edge[N];

void add(int u,int v,int w) {	//Connecting point u and point v 
	edge[u].push_back({v,w});
//	edge[v].push_back({u,w}); 	 This paragraph needs to be added to the undirected graph 
}

int main() {
	while(cin>>n>>m&&n!=0&&m!=0) {	//Multiple case output 
		int u,v,w;	//The distance between point u and point v is w 
		for(int i=0; i<m; i++) {
			cin>>u>>v>>w;
			add(u,v,w);
		}
		for(int i=1; i<=n; i++) {	//All the points have not been determined at present 
			vs[i]=0;
		}
		for(int i=1; i<=n; i++) {	//All points are now infinitely away from the starting point 
			d[i]=INF;
		}
		d[1]=0;	//The distance between the starting point and yourself is 0 
		int x;	//Record the shortest point to the starting point 
		for(int i=1; i<=n; i++) {	//n vertices 
			x=0,m=INF;	 
			for(int j=1; j<=n; j++) {	//Find the point closest to the starting point 
				if(!vs[j]&&d[j]<=m) {
					m=d[j];	//Refresh minimum 
					x=j;	//record 
				}
			}
			if(m==INF) {	//If the current minimum value is infinity, it means that other points are not connected with the starting point and can exit directly 
				break;
			}
			vs[x]=1;	//Determine the value of this point found so far 
			for(int j=0; j<edge[x].size(); j++) {	//Relax all the points connected to x
//				The distance from the point connected to x directly to the starting point, and the distance to x + the distance from X to the point connected to X 
				d[edge[x][j].to]=min(d[edge[x][j].to],d[x]+edge[x][j].w);
			}
		}
		cout<<d[n]<<endl;
		memset(d,0,sizeof(d));
		memset(edge,0,sizeof(edge));
	}

	return 0;
}

ending

I'm afraid of graph theory because I know nothing about graph theory
I'm different now

This blog post is original, except for the picture