Storage and traversal of ordinary trees

Posted by MindOverBody on Tue, 15 Feb 2022 11:26:55 +0100

Pre knowledge: the concept of tree and vector

In order to ensure the learning effect, please ensure that you have mastered the pre knowledge before learning this chapter!

Learning objectives

Understand the idea, implementation, advantages and disadvantages of several storage methods of tree
Master the code implementation of the storage method of the tree
Master two traversal methods of tree: first root traversal (DFS) and hierarchical traversal (BFS)

introduce

Obviously, the definition of {tree} is recursive, which is a recursive data structure. As a logical structure, tree is also a {hierarchical structure, which has the following two characteristics:

1) The root node of the tree has no precursor node, and all nodes except the root node have and only one precursor node.

2) All nodes in the tree can have zero or more successor nodes.

Storage with root tree

Father notation

In addition to the root node, other nodes have only one parent node. Therefore, we can store each tree edge on its child nodes in the form of: ii ， node's father is ， jj ， node, as shown in the figure below.

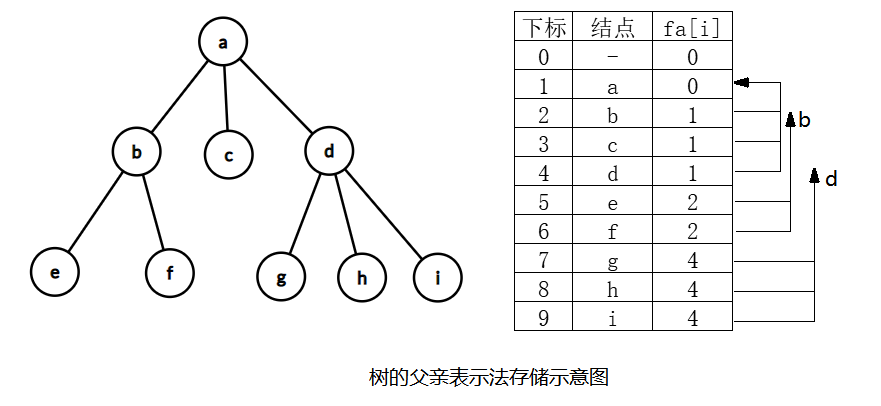
The basic implementation code of the storage structure of the parent representation is as follows:

int fa[N];
fa[a] = 0;     // Indicates that a is the root, or - 1 indicates that the parent node does not exist, depending on the writing method of the code
fa[x] = y;     // Connect X and y, and the parent node of node x is y

Copy

If the node information needs to be saved, it can be defined as a structure to realize:

struct node{
    int data;            // Node information, or other data types
    int father;          // Parent node number
}
node tree[N];            // Define a tree
void link(int x, int y)  // The parent node of x is y
{
    tree[x].father = y;  // Connect x and y
}

Copy

Advantages: save space, and for any node, you can easily find its parent node;

Disadvantages: finding child nodes is very troublesome and needs to traverse all nodes;

The father representation is the most space-saving, and the later learning "parallel search set" is to use this method to preserve the father son relationship on the tree.

Child representation

For each node, there is a data field and multiple pointer fields. The data field saves the data of the current node, and each pointer in the pointer field points to a child node, such as the following figure:

The example code of structure writing method is as follows:

struct node{
    int data;                // Node information, or other data types
    vector<int> children;      // All child node numbers
}
node tree[N];                // Define a tree
void link(int x, int y)      // The parent node of x is y
{
    tree[y].children.push_back(x);  // Connect x and y
}

Copy

Advantages: for any node, you can easily find all its child nodes;

Disadvantages: finding the parent node is very troublesome and needs to traverse all nodes;

Father child representation

Combining the advantages of the above two representation methods, each node not only saves its own information, but also saves the parent node and child node information of the current node. The example code is as follows:

struct node{
    int data;                // Node information, or other data types
    int father;              // Parent node number
    vector<int> children;      // Child node list
}
node tree[N];                // Define a tree
void link(int x, int y)      // The parent node of x is y
{
    tree[x].father = y;      // Connect x and y
    tree[y].children.push_back(x);  // Connect y and x
}

Copy

If you need to know the parent and child nodes of a node at the same time in the problem, you can use this writing method.

Child brother representation*

In the tree structure, nodes in the same layer are brother nodes to each other. For example, in the ordinary tree in the figure above, nodes A, B and C are brothers to each other, while nodes D, E and F are brothers to each other.

The child brother representation adopts a chain storage structure. The implementation idea of its storage tree is to start from the root node of the tree and store the child nodes and brother nodes of each node with a linked list in turn.

Therefore, the nodes in the linked list should contain the following three parts (as shown in the figure below):

The value of the node;
Pointer to child node;
Pointer to sibling node;

The example code is as follows:

struct node{
    int data;                // Node information, or other data types
    node* children;        // children
    node* brothers;      // Brothers
}

Copy

The following figure is the result of storing the tree in the above example using the child brother representation. It can be found that the ordinary tree represented by the child brother representation has been transformed into a binary tree for storage. Therefore, it can be concluded that any ordinary tree can be transformed into a binary tree through the child brother representation. In other words, Any ordinary tree has a unique binary tree corresponding to it.

Therefore, the representation of children's brothers can be used as the most effective method to convert an ordinary tree into a binary tree, which is often called "binary tree representation" or "binary linked list representation".

Storage method of graph with root tree*

A tree is actually a special kind of graph. We can regard a tree edge as a directed edge from the father to the son (or the son to the father). Therefore, the storage method of graph can also be used to store tree. The storage of graph includes adjacency matrix, adjacency list and chained forward star (special adjacency list). The specific methods will be learned later, and only a brief description will be given here.

adjacency matrix

Use a {n × nn × If the bool array of n  mpmp, mp[x][y]mp[x][y] is true, it means that there is a directed edge from X to y; otherwise, it means that there can be no such directed edge.

The storage code of adjacency matrix is as follows:

bool mp[N][N];
void link(int x, int y)
{
    mp[x][y] = 1;   // There are directed edges from x to y
}

Copy

Adjacency table

Similarly, we can use the adjacency table to store multiple tree edges connected by one point, as shown in the figure below.

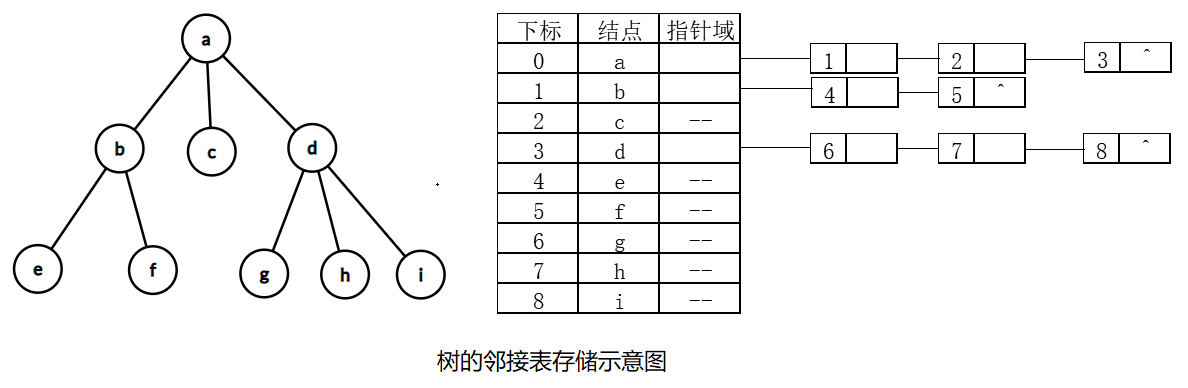
The storage code of adjacency table of STL Vector container vector using C + + is as follows:

vector<int> g[N];    // g[i] save and the out edge of node i

void link(int x, int y)  // Connect an edge from x to y. in the tree, x is the parent node of Y
{
    g[x].push_back(y);
}

Copy

Chain forward star*

In fact, the chained forward star is a statically established adjacency table. The time efficiency is  O(m)O(m), the space efficiency is  o (m), and the traversal efficiency is  o (m). mm  represents the number of edges. Chained forward star storage is suitable for all kinds of graphs, but it can not quickly query whether an edge exists, nor can it be convenient to sort the edges of a point.

The example code of chained forward star storage tree is as follows:

int cnt;            // Total number of edges
struct node{
    int to;         // Stores the number of the child that the current edge points to
    int next;       // Point to the next brother of the current son
} edge[N];          //
int head[N];        // The number of the last son of the storage node

void link(int x, int y)
{
    edge[cnt].to = y;
    edge[cnt].next = head[x];
    head[x] = cnt++;
}

Copy

Graph storage without root tree*

Because rootless trees have no definite roots, there is no clear distinction between father and son at the edge of the tree, so there is no clear direction. Therefore, the storage of rootless tree is generally stored in the way of undirected graph. When saving a drawing, for each edge connected, the corresponding two edges should be stored at the same time. The example code is as follows:

int cnt;            // Total number of edges
struct node{
    int to;         // Stores the number of the child that the current edge points to
    int next;       // Point to the next brother of the current son
} edge[N*2];
int head[N];        // head[i]: the number of the last son of node I

void link(int x, int y)
{
    edge[cnt].to = y;
    edge[cnt].next = head[x];
    head[x] = cnt++;
}

Copy

Traversal of tree

definition

Traversal of the tree refers to starting from the root node and accessing all nodes in the tree in a certain order, so that each node is accessed only once. Common traversal methods are: first root traversal (DFS) and hierarchical traversal (BFS).

preorder traversal

Traversal rules:

If the tree is empty, stop traversal;
If the tree is not empty, access the root node first, and then traverse all subtrees of the root node in turn.

It can be seen that root first traversal is a depth first traversal.

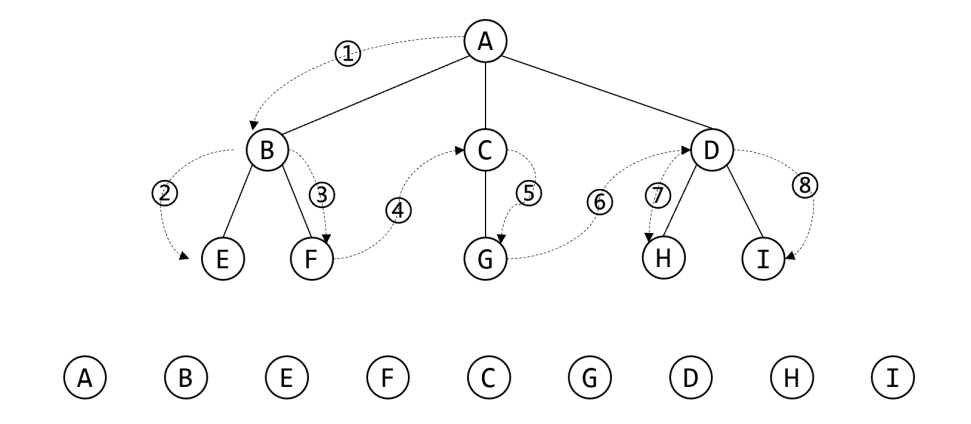
Code framework:

// Depth first traversal tree
void dfs(int root)
{
    // 1 - process the current node, such as output
    ......
    // 2 - expand the new node, that is, traverse all child nodes
    for(int i = 0; i < tree[root].son.size(); i++)
    {
        dfs(tree[root].son[i]);  // Child nodes into "function stack"
    }
}

Copy

level traversal

Traversal rules:

If the tree is empty, stop traversal.
If the tree is not empty, the access starts from the first layer of the tree, that is, the root node, and is accessed layer by layer from top to bottom. In the same layer, the nodes are accessed one by one from left to right.

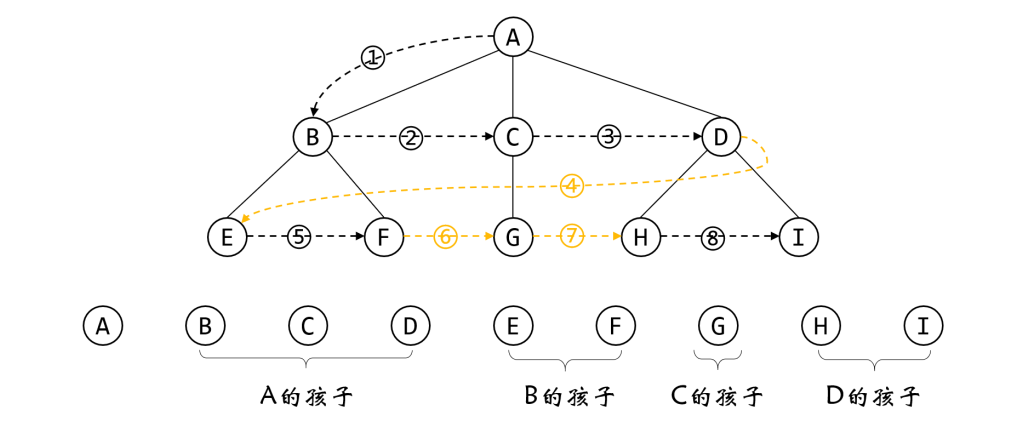
If a node is accessed first, its child nodes will also be accessed first. If the access itself is regarded as in and the access child nodes are regarded as made, the hierarchical traversal rules meet the first in, first out.

It can be seen that hierarchical traversal is a breadth first traversal.

Code framework:

void bfs(int root)
{
    queue<int> q;        // 1 - define queue
    q.push(root);        // 2 - root node join
    while(!q.empty())    // 3 - as long as the queue is not empty:
    {
        // (1) Take out the first node of the queue and process the current node, such as output
        int k = q.front();      
        q.pop();
        ......
        // (2) Expand the new node, that is, traverse all child nodes
        for(int i = 0; i < tree[k].son.size(); i++)
        {
            q.push(tree[k].son[i]);  // Child nodes join the queue
        }
    }
}

Copy

summary

1. There are many storage methods for trees. Each method has its own advantages and disadvantages. The comparison is as follows:

	Parent or child representation	Parent child representation	adjacency matrix	Adjacency table	Chain forward star
advantage	Easy to understand, minimum storage space consumption	Easy to understand	Simple implementation	The utility model has the advantages of simple implementation and small space consumption, and is suitable for various occasions	Small space consumption, suitable for all occasions
shortcoming	The amount of information stored is small and many operations are inconvenient	Save parent and child nodes at the same time, which consumes more space O(2n)O(2n)	Huge space consumption, O(n^2)O(n2), suitable for dense graphs	Need to master vector operation	It is difficult to understand and cannot quickly query edges and sort the outgoing edges of a point

2. The traversal of the tree deeply reflects the importance of depth first search and breadth first search. DFS and BFS are widely used in trees and must be mastered.