catalogue
II Storage of integers in memory
III Storage of floating point in memory
I data type

(1) Integer type: char, short, int, long
These types are also divided into signed and unsigned, such as signed char and unsigned char
Among them, short, int and long are unsigned by default in the compiler, and whether char is signed or unsigned by default depends on the compiler
The range of signed char is - 128 to 127, and the range of unsigned char is 0 to 255
(2) Floating point type: float, double, long double
(3) Construction type (custom type):
^Array type
^Structure type struct
^Enum type enum
^Union type union
(4) Pointer type
For example: int *p, char *str
(5) Empty type void
It is usually used for the return type, parameter and pointer type of a function
II Storage of integers in memory
(1) Original code, inverse code and complement code
1. The original code, inverse code and complement of positive integer are the same
Data is stored in memory as a complement
Calculation 1-1 Calculate with original code 1 Original code of:00000000 00000000 00000000 00000001 -1 Original code of:10000000 00000000 00000000 00000001 because CPU There is only adder in, so 1-1 Will be converted to 1+(-1) Calculation results:10000000 00000000 00000000 00000010 Convert to decimal-2 Calculate with inverse code 1 Inverse code of:00000000 00000000 00000000 00000001 -1 Inverse code of:11111111 11111111 11111111 11111110 Calculation results:11111111 11111111 11111111 11111111 Convert to decimal-1 Calculation with complement 1 Complement of: 00000000 00000000 00000000 00000001 -1 Complement of: 11111111 11111111 11111111 11111111 Calculation results:1 00000000 00000000 00000000 00000000 Because only 32 can be stored bit So it will be lost Convert to decimal 0
2. Three code conversion of negative integer:
Original code: directly translate the numerical value into binary in the form of positive and negative numbers.
Inverse code: the sign bit of the original code remains unchanged, and other bits are obtained by inverting the bit in turn
Complement: inverse code + 1 will get complement
Negative integer from complement to original
Method 1: subtract one from the complement, and then the sign bit remains unchanged, and the other bits are reversed by bit
Method 2: the complement symbol bit remains unchanged, the other bits are reversed by bit, and then one is added
#include<stdio.h>
int main()
{
unsigned int ch = -10;
//10000000 00000000 00000000 00001010
//11111111 11111111 11111111 11110101
//11111111 11111111 11111111 11110110
printf("%u",ch);
printf("%d",ch);
return 0;
}%u is to print unsigned number, which means that what you want me to print must be unsigned number, not unsigned number. I also think it is unsigned number
%d , is the signed number printed, which means that what you want me to print must be the signed number, not the signed number. I also think it is the signed number
Operation results: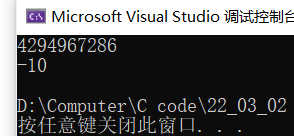
4294967286 is the complement of - 10
(2) Large and small end introduction
What big end and small end:
Large end (storage) mode means that the low order of data is saved in the high address of memory, while the high order of data is saved in the low address of memory;
Small end (storage) mode means that the low order of data is saved in the low address of memory, while the high order of data is saved in the high address of memory.

How to judge the big end and small end of the compiler
#include<stdio.h>
int x(int *a)
{
if (*a && 1 == 1)//Bitwise and the first byte with 1
{
return 1;
}
else
return 0;
}
int main()
{
int a = 0x01;//a's address
int ret=x(&a);
if (ret == 1)
printf("Small end");
else
printf("Big end");
return 0;
}(3) integral lifting
#include<stdio.h>
int main()
{
char a = -1;
// -1
//Original code: 1000000000000001
//Inverse code: 11111111111111111111111111111111111110
//Complement: 11111111111111111111111111111111111
//char has only one byte and can only store 11111111
//Because% d prints integer data and a is signed, and the sign bit is 1, a must first promote the integer and supplement 1 when promoting
//After lifting: 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111
signed char b = -1;//b is the same as a
unsigned char c = -1;
//Because c is an unsigned numeric character type, it is a positive number,% d. before printing, integer promotion shall be carried out, and 0 shall be supplemented during promotion
//11100000011: 111000000255
printf("a=%d,b=%d,c=%d\n", a, b, c);
return 0;
}Operation results:
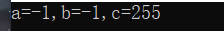
III Storage of floating point in memory
There are two representations of floating point numbers: 2.96, 2e3
Floating point storage rule
According to the international standard IEEE 754, any binary floating-point number V can be expressed in the following form:
(-1)^S * M * 2^E
(- 1)^s represents the sign bit. When s=0, V is a positive number; When s=1, V is negative.
M is a significant number, greater than or equal to 1 and less than 2. 2^E represents the exponential bit.
Convert the decimal system into binary system, and the first digit after the decimal point is 2 ^ - 1,2 ^ - 2
So convert 5.5 to binary to 101.1
Because 5.5 is an integer, S=0, M is 101.1, E is 2101.1, which is converted to 1.01 * 2 ^ 2
To sum up, 5.5 = (- 1) ^ 0 * 1.011 * 2 ^ 2
IEEE 754 stipulates:
For 32-bit floating-point numbers, the highest bit is sign bit s, the next 8 bits are exponent E, and the remaining 23 bits are significant digits M.
For 64 bit floating-point numbers, the highest bit is sign bit S, the next 11 bits are exponent E, and the remaining 52 bits are significant digits M.
IEEE # 754 # has some special provisions on the significant number # M # and index # E.
As mentioned earlier, 1 ≤ M < 2, that is, M ^ can be written as ^ 1 The form of xxxxxx , where , xxxxxx , represents the decimal part.
IEEE 754 stipulates that when saving M in the computer, the first digit of this number is always 1 by default, so it can be rounded off and only the following xxxxxx part is saved. For example, when saving # 1.01 # only save 01. When reading, add the first # 1 # to it. The purpose of this is to save 1 # significant digits.
Take the ^ 32 ^ bit floating-point number as an example, leaving M ^ only ^ 23 ^ bits. After rounding off the 1 ^ of the first bit, it is equal to saving ^ 24 ^ significant digits.
As for index E, the situation is more complicated.
First, E , is an unsigned integer (unsigned , int)
This means that if E is 8 bits, its value range is 0 ~ 255; If E is 11 bits, its value range is 0 ~ 2047. However, we know that E , in scientific counting can be negative,
Therefore, IEEE 754 stipulates that the real value of E must be added with an intermediate number when stored in memory. For E with ^ 8 ^ bits, this intermediate number
Is 127; For E of ^ 11 ^ the median is ^ 1023.
For example, E of 2 ^ 10 is 10, so when saving as a 32-bit floating-point number, it must be saved as 10 + 127 = 137, that is
10001001 .
The computer only stores the values of S, E and M.
#include<stdio.h>
int main()
{
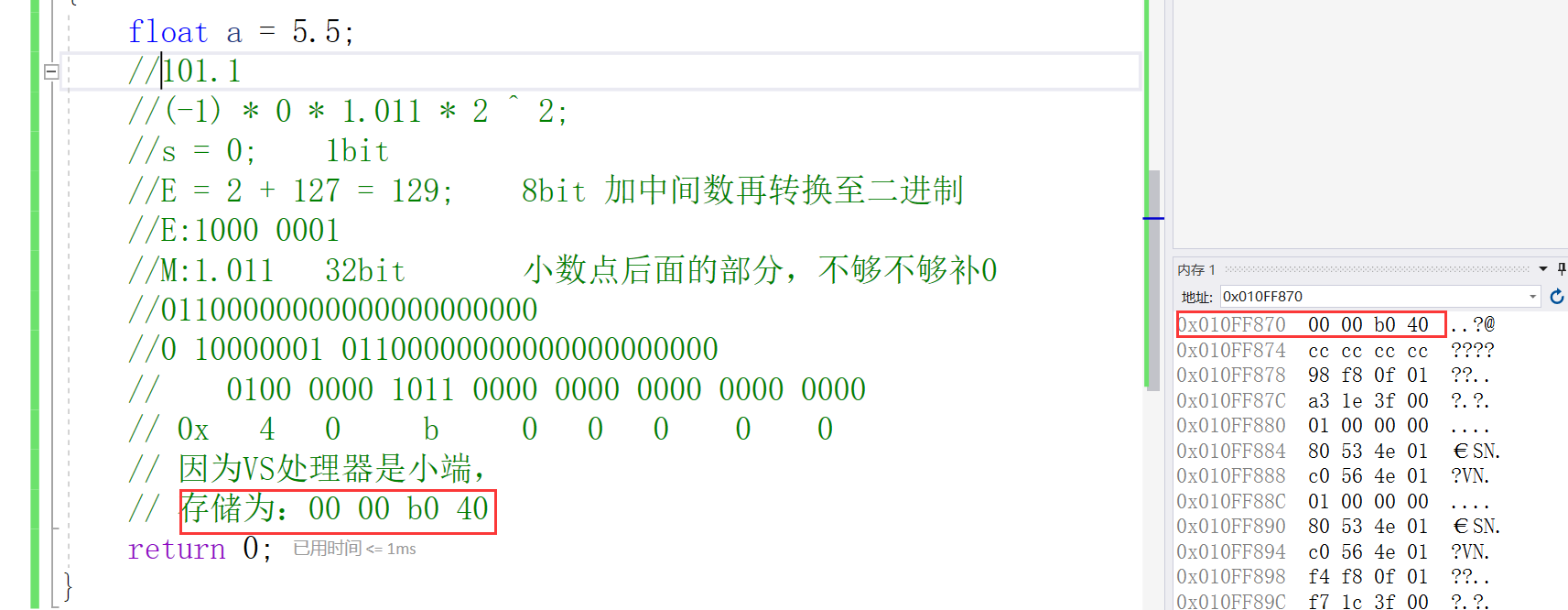
float a = 5.5;
//101.1
//(-1) * 0 * 1.011 * 2 ^ 2;
//s = 0; 1bit
//E = 2 + 127 = 129; 8bit plus the middle number and then converted to binary
//E:1000 0001
//M:1.011 32bit The part after the decimal point is not enough to make up 0
//01100000000000000000000
//0 10000001 01100000000000000000000
// 0100 0000 1011 0000 0000 0000 0000 0000
// 0x four 0 b 0 0 0 0 0 to hexadecimal.
// Because the VS processor is a small end,
// Stored as: 00 00 b0 40
return 0;
}
Index E can be extracted from memory in three cases:
E , not all , 0 , or not all , 1
At this time, the floating-point number is represented by the following rule, that is, the calculated value of index E minus 127 (or 1023) to obtain the real value, and then
The significant number M is preceded by the first 1 .
For example:
The binary form of 0.5 (1 / 2) is , 0.1. Since it is specified that the positive part must be , 1, that is, the decimal point is shifted to the right by , 1 , then
1.0 * 2 ^ (- 1), its order code is - 1 + 127 = 126, expressed as
01111110, and the mantissa of 1.0 is 0, the integer part is 0, and the complement of 0 to 23 bits of 00000000000000000000000000000 is binary
The system is expressed as:
0 01111110 00000000000000000000000
E , all 0
At this time, the exponent E of the floating point number is equal to 1-127 (or 1-1023), which is the real value,
The significant number , M , is no longer added with the first , 1, but , is restored to 0 The decimal of XXXXXX. This is done to represent ± 0 and a small number close to , 0 ,.
E ^ all are ^ 1
At this time, if the significant digits ^ M ^ are all ^ 0, it means ± infinity (the positive and negative depend on the sign bit ^ s);
Example:
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n The value of is:%d\n", n);
printf("*pFloat The value of is:%f\n", *pFloat);
*pFloat = 9.0;
printf("num The value of is:%d\n", n);
printf("*pFloat The value of is:%f\n", *pFloat);
return 0;
}
Operation results:
The inverse code of n is 00000000000000000000001001
So, printf ("the value of n is:% d\n", n); The value of / / N is: 9
Casts an integer to a single precision floating-point type.
*pFloat 0 00000000 00000000000000000001001
Because it is converted into floating-point number, it is extracted by floating-point number extraction.
E = -126, M = 0.00000000000000000001001, S = 0
Namely: (- 1) ^ 0 * 0.00000001001 * 2 ^ (- 126)
We know that%f stores 6 decimal places after the decimal point by default. Just one M is rounded to zero, not to mention multiplying by another
2^(-126)
printf("*pFloat value is:% f\n", * pFloat); / / * the value of pFloat is: 0.000000
* pFloat = 9.0;
Storage is stored in the form of floating point numbers.
9.0
1001.0
1.001 * 2^3
(-1)^0 * 1.001 * 2^3
S = 0
M = 1.001
E = 3 +127
0 10000010 00100000000000000000000
In case of integer printing, the computer regards it as complement.
0 is a sign bit and a positive number.
Positive number, original, inverse and complement are the same
And the above numbers are converted to decimal