Violence matching method

If the idea of violent matching is used, and assuming that str1 is now matched to position i and substring str2 is matched to position j, there are:

1. If the current character matches successfully (i.e. str1[i] == str2[j]), then I + +, j + +, continue to match the next character
2. If mismatch (i.e. STR1 [i]! = STR2 [J]), let i= i - (j - 1), j = 0; It is equivalent to I backtracking and J being set to 0 every time a match fails
3. If violence is used to solve the problem, there will be a lot of backtracking. Only move one bit at a time. If it does not match, move to the next bit and then judge, wasting a lot of time
4. Implementation of violence matching algorithm

package KMP;
// Implementation of violence matching algorithm
public class ViolenceMatch {
    public static void main(String[] args) {
        String str1 = "jaklsdjaowijdlkaj";
        String str2 = "jao";
        System.out.println(violenceMatch(str1, str2));
    }
    // Violence matching algorithm
    public static int violenceMatch(String str1, String str2){
        char[] s1 = str1.toCharArray();
        char[] s2 = str2.toCharArray();
        int s1Len = s1.length;
        int s2Len = s2.length;
        int i = 0, j = 0;
        while (i < s1Len && j < s2Len){
            if (s1[i] == s2[j]) {
                i++;
                j++;
            } else { // No match succeeded
                // If it fails, move i backward one bit forward and reset j to 0
                i = i - (j - 1);
                j = 0;
            }
        }
        if(j == s2Len){
            return i-j;
        }else {
            return  -1;
        }

    }
}

KMP

The KMP algorithm uses the previously judged information to save the length of the longest common subsequence in the pattern string through a next array. Each time, it finds the matching position through the next array, saving a lot of calculation time

The key of KMP is to find repeated substrings and common subsequences. Take "ABCDABD" as an example:

First, we get A, its prefix is not, its suffix is not so, and naturally there is no repeated common subsequence

Then we read a B and formed an "AB" string with the previous A. its prefix has {"a"} and suffix has {"B"}. Obviously, there is no repetition between prefix and suffix, so there is no repetition of common subsequence

After that, we read A C and formed an "ABC" string with the previous "AB". Its prefix has {"A", "AB"}, and its suffix has {"C", "BC"}. Obviously, neither prefix nor suffix is repeated, so there is no repeated common subsequence

Read on and read A D. it forms "ABCD" with the previous "ABC". Its prefix has {"A", "AB", "ABC"}, and its suffix has {"d", "CD", "BCD"}. Obviously, there is no repetition of prefix and suffix, so there is no repetition of common subsequence

Next, we continue to get an A and form an "ABCDA" string. Its prefix has {"a", "AB", "ABC", "ABCD"}, and its suffix has {"a", "DA", "CDA", "BCDA"}. At this time, we see that there is an "a" between the prefix and suffix, which is the repeated common subsequence between them. We mark a 1 at the current position

Next, continue reading and get B, which forms "ABCDAB". The prefix is {"A", "AB", "ABC", "ABCD", "ABCDA"}, and the suffix is {"B", "AB", "DAB", CDAB "," BCDA "}. We find that its prefix and suffix have A common subsequence, that is" AB ", so we mark the current position as 2 (because the length of" AB "is 2)

Next, continue to read and get D, which forms "ABCDABD". The prefix is {"A", "AB", "ABC", "ABCD", "ABCDA", "ABCDAB"}, and the suffix is {"d", "BD", "ABD", "DABD", CDABD "," BCDAD "}. We find that there is no common subsequence for its prefix and suffix

Here we get a table: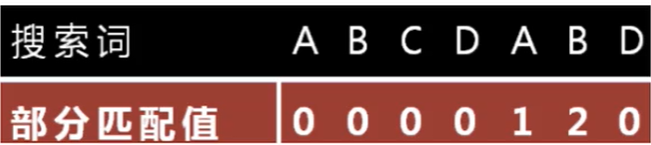

package KMP;

import java.util.Arrays;

// KMP
public class KMPAlgorithm {
    public static void main(String[] args) {
        String str1 = "BBC ABCDAB ABCDABCDABDE" ;
        String str2 = "ABCDABD";

        int[] next = kmpNext(str2);
        System.out.println(Arrays.toString(next));
        int index = kmpSearch(str1, str2, next);
        System.out.println(index);
    }

    // Gets a partial matching value of a string (substring)
    public static int[] kmpNext(String dest){
        // Create a next array and save some matching values
        int[] next = new int[dest.length()];
        next[0] = 0; // If dest has only one character, the matching value of that part is 0
        for (int i = 1, j = 0; i < dest.length() ;i++){
            while (j > 0 && dest.charAt(i) != dest.charAt(j)){
                // We need to get a new j from next[j-1]
                // We didn't launch until we found satisfaction
                j = next[j - 1];
            }
            // When this condition is met, the partial matching value is + 1
            if (dest.charAt(i) == dest.charAt(j)){
                j++;
            }
            next[i] = j;
        }
        return next;
    }
    // search algorithm 
    public  static  int kmpSearch(String str1, String str2, int[] next){
        for (int i = 0, j = 0; i < str1.length(); i++) {
            // We need to consider when two are not equal
            if(j > 0 && str1.charAt(i) != str2.charAt(j)){
                j = next[j - 1];
            }
            if(str1.charAt(i) == str2.charAt(j)){
                j++;
            }
            if(j == str2.length()){
                return i - j + 1;
            }
        }
        return -1;
    }
}