Suffix Automaton

Title Description

Logu P3804

Core ideas

Consider how to find the number of occurrences of substrings

Conclusion: Number of substrings =|endpos(substr)|

That is, the number of substrings that occur is actually the number of elements in the endpos(substr) collection

Perceptual understanding as follows:

As shown in the figure above, set the original string to a b c a abca abca, we want to ask for the number of substrings a, the original string can see that substring a appears twice at a glance. But when we look at endpos, e n d p o s ( " a " ) = [ 1 , 4 ] endpos("a")=[1,4] endpos("a")=[1,4], the number of elements in this set is 2, which just indicates that substring a appears twice.

Next, consider how you can find the size of an endpos set.

Note here that the endpos collection is actually only related to the suffix link link in the suffix automaton, so when we draw, we just need to establish the edge that contains the link.

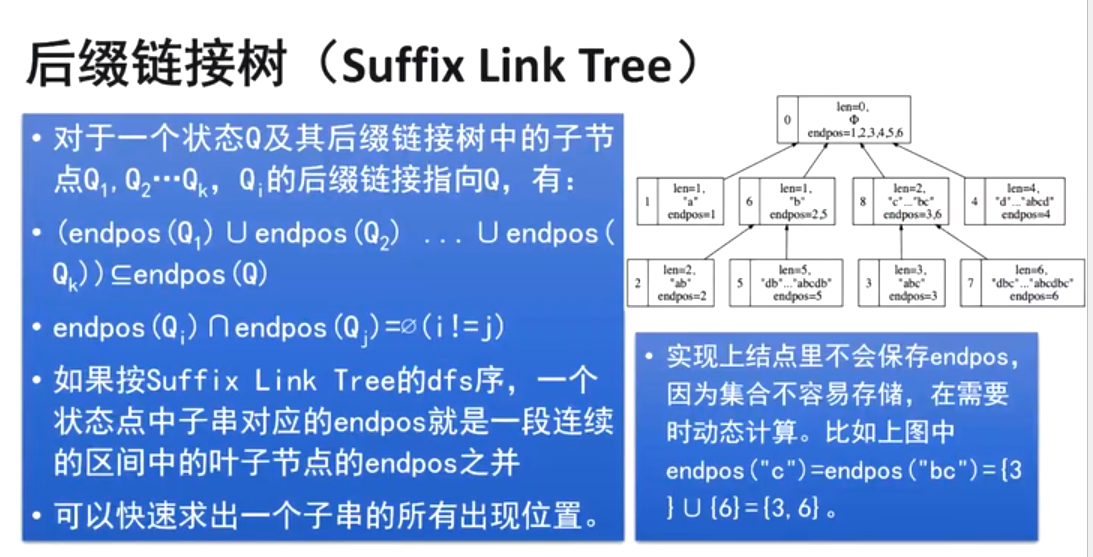
As shown in the figure above, we find a property: the union of leaf node endpos constitutes the element in their parent node endpos. However, be aware that it is possible that the parent node has its own unique elements. So to calculate the size of endpos[u], first calculate the size of its own unique element endpos[u], then calculate the element size of its child nodes endpos[v], then add up and you get the state node u u The size of the endpos collection of u ∣ e n d p o s ( u ) ∣ |endpos(u)| ∣endpos(u)∣

Although in the suffix automaton, we refer to the suffix link edge from the child node to the parent node, in this topic, we construct a directed edge from the parent node to the child node. Why? So when we do dfs, we recurse from the root node to the leaf node, and then we count the leaf nodes v v endpos collection size of v e n d p o s ( v ) endpos(v) endpos(v), then it will be added back to its parent node u u u, then the parent node can be calculated u u endpos collection size of u e n d p o s ( u ) endpos(u) endpos(u)

Code

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
//N is the number of state nodes in the suffix automaton to be doubled M is the total number of edges in the graph when only link suffix links are established
const int N = 2e6+10,M = N;
//tot records the state node in the suffix automaton initialized to root node 1
//Last records the last status node
int tot = 1, last = 1;
struct Node
{
    int len;    //Record the length of the largest string in the string formed by this state node
    int link;   //Suffix Links
    int ch[26]; //Like a child in a trie tree
}node[N];
char str[N];
//The endpos collection ans is the answer
LL endpos[N], ans;  
int h[N], e[M], ne[M], idx;

//Suffix Auto Template
void extend(int c)
{
    //Use p to record the last status node first
    //Then, because a character c comes in, a state transition is needed
    // So assign a number tot to the node np that is transferred
    int p = last, np = last = ++ tot;
    //A string ending at tot is itself a prefix
    endpos[tot] = 1;
    //Since np is transferred from p to the past by adding a new character c, this length+1
    node[np].len = node[p].len + 1;
    //Traverse nodes along the suffix link of p If the traversed node p has no children c
    //Then create a suffix link for np to node[p].ch[c] is equivalent to
    //The node p is moved to np by the character c
    for (; p && !node[p].ch[c];p = node[p].link)
        node[p].ch[c] = np;
    //Following the suffix link to the root node is still not found
    //Then the np suffix link is the root node
    if (!p)
        node[np].link = 1;
    else
    {
        int q = node[p].ch[c];  //Find c child node q of state node p
        //np finds q along the suffix link and finds that np wants a string in q that can be suffixed adjacent
        //Then nq can draw a suffix link to q
        if (node[q].len == node[p].len + 1)
            node[np].link = q;
        else
        {
            //Divide q into q and nq
            int nq = ++ tot;
            //nq is cloned from q, but nq contains a string that is pulled from Q and suffixed by np
            node[nq] = node[q], node[nq].len = node[p].len + 1;
            //Quote a suffix link to nq before splitting
            //Quote a suffix link from the newly opened state node np to nq
            node[q].link = node[np].link = nq;
            //Go back and forth along the suffix link of p to quote a suffix link to the nq at all the nodes traversed
            for (; p && node[p].ch[c] == q; p = node[p].link)
                node[p].ch[c] = nq;
        }
    }
}

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int v=e[i];
        dfs(v);
        //The endpos of the current state node u is equal to its own unique endpos[u] plus the endpos[v] of its child node
        //For example, u={1,2,3,4,5} v1={1,2}, v2={3,4} is unique to {5}
        //So the number of elements in the endpos set of u is its own unique {5} plus |v1|+|v2|
        //There are five elements, endpos[u], with five elements
        endpos[u] += endpos[v];
    }
    //Number of occurrences is not 1
    if (endpos[u] > 1) 
        ans = max(ans, endpos[u] * node[u].len);
}

int main()
{
    scanf("%s", str+1);
    for (int i = 1; str[i]; i ++ )
        extend(str[i] - 'a');
    memset(h, -1, sizeof h);
    //Although a suffix link in a suffix automaton leads from a child node to a parent node
    //But we're building edges from parent to child because
    //When we dfs, we recurse from the parent node to the child node and then count the endpos value of the child node
    //This adds up to the endpos of its parent node when backtracking, which satisfies the nature of "the parent is the union of its children"
    for (int i = 2; i <= tot; i ++ )
        add(node[i].link, i);
    dfs(1); //Start deep search from the root node of the suffix state machine
    printf("%lld\n", ans);

    return 0;
}