B
subject
Use n-1 roads to link n cities. Each city has its own value ai. When building roads, it will lose the value of gcd(ai,aj). What is the minimum loss value
Unlike before, random numbers are generated, and the data is large

thinking
At first, I thought that the minimum spanning tree would time out, but I couldn't think of another way, so I..
If you directly type the table or try, you will find that when n is very large, the result is n-1 (probably because of the distribution law of prime numbers. With the increase of numbers, prime numbers will increase, and gcd is easy to appear 1)
Then, after the table is printed, the minimum spanning tree is used before 1000, and after 1000, it can be directly output in n-1
It should also be noted that when L=R, it also directly outputs (n-1) * L
code
#include <bits/stdc++.h>
#define maxx 201100
#define inf 0x3f3f3f3f
typedef long long ll;
using namespace std;
int n, L, R, a[maxx];
unsigned long long seed;
//create
unsigned long long xorshift()
{
unsigned long long x = seed;
x ^= x << 13;
x ^= x >> 7;
x ^= x << 17;
return seed = x;
}
int gen()
{
return xorshift() % (R - L + 1) + L;
}
int gcd(int a, int b)
{
while (b)
{
int t = b;
b = a % b;
a = t;
}
return a;
}
//kruskal
int fa[1100];
int cnt = 1;
struct edge
{
int from, to, l=999999999;
} e[1100];
bool cmp(edge e1, edge e2)
{
return e1.l < e2.l;
}
void add(int x, int y, int l)
{
e[cnt].from = x;
e[cnt].to = y;
e[cnt].l = l;
cnt++;
}
int findd(int x)
{
if (fa[x] != x)
{
fa[x]=findd(fa[x]);
}
return fa[x];
}
int kruskal()
{
for (int i = 1; i <= n; ++i)
{
fa[i] = i;
}
sort(e+1,e+cnt+1,cmp);
int ans = 0;
int nn=0;
for (int i = 1; i <= cnt; ++i)
{
int x = e[i].from;
int y = e[i].to;
int ll = e[i].l;
int fx = findd(x);
int fy = findd(y);
if (fx!=fy)
{
fa[fy] = fx;
ans+=ll;
nn++;
}
if (nn==n-1)
break;
}
return ans;
}
int main()
{
scanf("%d%d%d%llu", &n, &L, &R, &seed);
if (L == R)
{
cout << 1ll*(n - 1) * L << endl;
return 0;
}
if (n > 1000)
{
cout<<n-1<<endl;
return 0;
}
for (int i = 1; i <= n; ++i)
{
a[i] = gen();
// cout << a[i] << endl;
}
for (int i = 1; i <= n; ++i)
{
for (int j = i + 1; j <= n; ++j)
{
int len = gcd(a[i], a[j]);
// cout<<len<<endl;
add(i,j,len);
add(j,i,len);
}
}
int ans = kruskal();
cout<<ans<<endl;
return 0;
}
C
subject
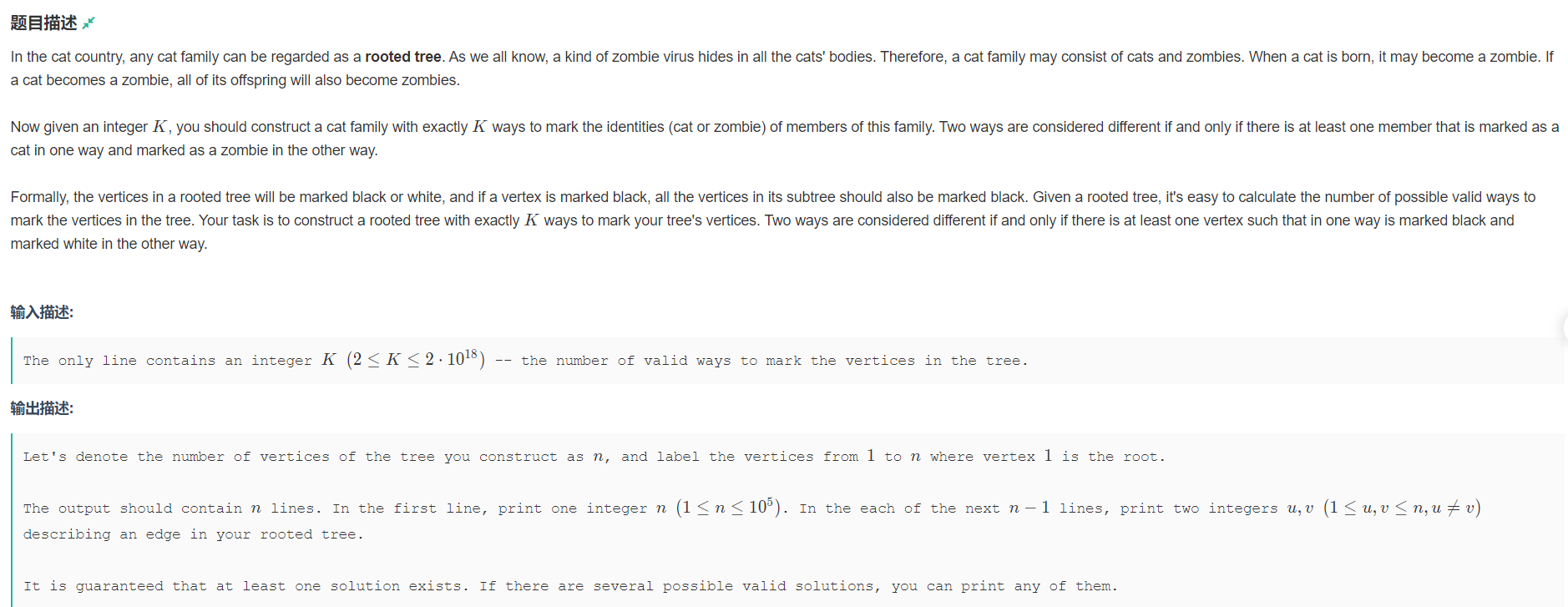
Construct a tree to meet k dyeing schemes
thinking
At the beginning, I thought that a direct string of nodes could meet the meaning of the question, but the range of n in the question is far less than the range of k, which is certainly not possible. So I used the least nodes to construct a tree that meets the conditions, and then found the law:
From odd to even: at root node + root node
From even to odd: pick up a node closest to the root node
I don't think I can see the solution. I can't think of it. Sobbing
code
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL k;
int main(){
cin>>k;
LL fa=1,id=1,tmp=k,cnt=1;
while(tmp>3){
if(tmp&1){
tmp/=2;
cnt+=2;
}
else{
tmp--;
cnt++;
}
}
if(tmp==3) cnt++;//Add one more point
cout<<cnt<<endl;
while(k>3){
if(k&1){//Odd number
k/=2;
id++;
cout<<fa<<" "<<id<<endl;//Left
id++;
cout<<fa<<" "<<id<<endl;//right
fa=id;
}
else{//Odd number
k--;
id++;
cout<<fa<<" "<<id<<endl;//right
fa=id;
}
}
if(k==3){
id++;
cout<<fa<<" "<<id<<endl;//Special judgment, even one on the right
}
}
D - Dyson Box
subject
Given a set of coordinates, place the blocks, and then move them all down or all to the left to find the perimeter of the figure after each placement
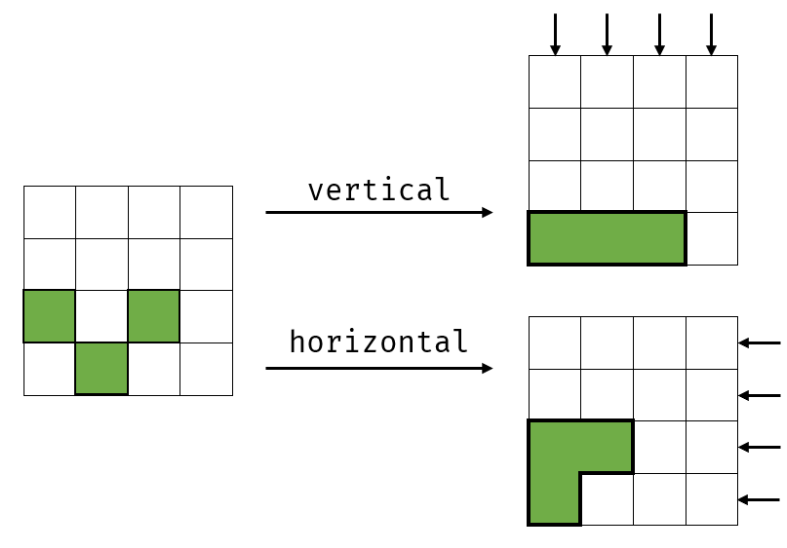
thinking
At first, the way to think about it was to put it once and find the law of each summation, but then it timed out. At first, I knew it was timed out, but I didn't want to think about other ideas, so I wasted some time.
The rule should be: the relationship between the circumference of each time and the circumference of the last time, so you don't have to calculate it every time~
code
#include <bits/stdc++.h>
#define maxx 200100
#define inf 0x3f3f3f3f
using namespace std;
int N;
int vx[maxx], vy[maxx];
int main()
{
cin >> N;
int sum1 = 0, sum2 = 0;
for (int i = 0; i < N; ++i)
{
int x, y;
cin >> x >> y;
//vertical
vx[x]++;
if (vx[x] > vx[x - 1] && vx[x] > vx[x + 1])
{
if (vx[x] == 1)
sum1 += 4;
else
sum1 += 2;
}
if (vx[x] <= vx[x - 1] && vx[x] <= vx[x + 1])
{
if (vx[x] != 1)
sum1 -= 2;
}
if (vx[x] <= vx[x - 1] && vx[x] > vx[x + 1])
{
if (vx[x]==1)
sum1 += 2;
}
if (vx[x] > vx[x - 1] && vx[x] <= vx[x + 1])
{
if (vx[x]==1)
sum1 += 2;
}
cout<<sum1<<' ';
//horizontal
vy[y]++;
if (vy[y] > vy[y - 1] && vy[y] > vy[y + 1])
{
if (vy[y] == 1)
sum2 += 4;
else
sum2 += 2;
}
if (vy[y] <= vy[y - 1] && vy[y] <= vy[y + 1])
{
if (vy[y] != 1)
sum2 -= 2;
}
if (vy[y] <= vy[y - 1] && vy[y] > vy[y + 1])
{
if (vy[y]==1)
sum2 += 2;
}
if (vy[y] > vy[y - 1] && vy[y] <= vy[y + 1])
{
if (vy[y]==1)
sum2 += 2;
}
cout<<sum2<<endl;
}
return 0;
}
H - Adventurer's Guild
subject
Two dimensional knapsack
thinking
At that time, I thought I didn't write because I didn't learn 2D backpack.. In fact, it's not difficult..
code
#include <bits/stdc++.h>
#define maxx 1100
#define inf 0x3f3f3f3f
typedef long long ll;
using namespace std;
int n, H, S;
ll f[maxx][maxx];
int main()
{
cin >> n >> H >> S;
ll ans = 0;
for (int i = 1; i <= n; ++i)
{
int h, s, w;
cin >> h >> s >> w;
for (int j = H; j > h; j--)
{
for (int k = S; k >= 0; k--)
{
if (j + k > h + s)
{
if (k < s) //stamina is not enough
{
f[j][k] = max(f[j][k], f[j - h - s + k][0] + w);
}
else
{
f[j][k] = max(f[j][k], f[j - h][k - s] + w);
}
}
}
}
}
cout << f[H][S] << endl;
return 0;
}
M - Matrix Problem
subject
Matrix C is obtained by the operation of matrices A and B. give matrix C and find a and B
Operation mode of AB: C is 1 only when all positions in AB are 1