Symmetric array problem
Generally, the array problem with symmetry can be solved by forward traversal and reverse traversal, such as 162 peak elements and 135 distribution elements
Distribute candy
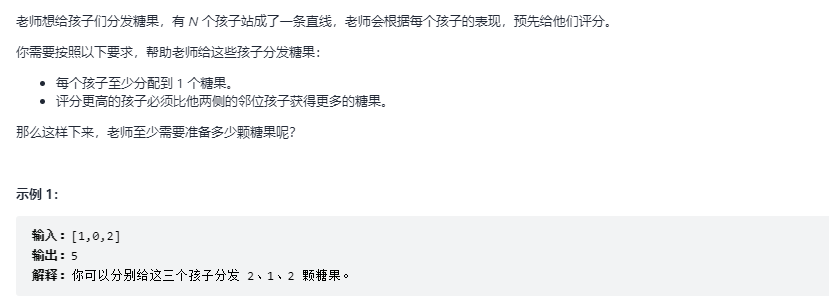
Use arrays Fill initializes all arrays to 1. During forward traversal, traverse the position from 1 to (n-1), and during reverse traversal, traverse the position from (n-2) to 0. When the current number is greater than the previous number, add 1 to the number of candy. Since the problem conditions require forward traversal and reverse traversal, the maximum value should be taken
public int candy(int[] ratings) {
int[] left = new int[ratings.length];
int[] right = new int[ratings.length];
Arrays.fill(left, 1);
Arrays.fill(right, 1);
for(int i = 1; i < ratings.length; i++)
if(ratings[i] > ratings[i - 1]) left[i] = left[i - 1] + 1;
int count = left[ratings.length - 1];
for(int i = ratings.length - 2; i >= 0; i--) {
if(ratings[i] > ratings[i + 1]) right[i] = right[i + 1] + 1;
count += Math.max(left[i], right[i]);
}
return count;
}Longest continuous sequence
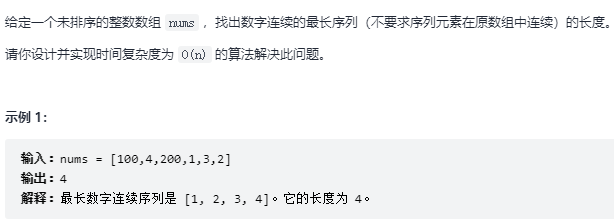
The hash table is used to solve this problem. Starting from the minimum number each time, it can ensure that duplicate results are not calculated. The minimum numbers in the above example are 1.100 and 200 respectively, so the results can be obtained as long as they are calculated three times
public int longestConsecutive(int[] nums) {
Set<Integer> num_set = new HashSet<Integer>();
for (int num : nums) {
num_set.add(num);
}
int longestStreak = 0;
for (int num : num_set) {
//Enter only when there is no smaller number than it, and ensure that each update sequence starts from the smallest
if (!num_set.contains(num - 1)) {
int cur = num;
int res = 1;
//The sequence length is continuously updated from the minimum value of a sequence
while (num_set.contains(cur + 1)) {
cur += 1;
res += 1;
}
longestStreak = Math.max(longestStreak, res);
}
}
return longestStreak;
}Verify that a sentence is a palindrome string

Verifying the palindrome string is very simple. Just use double pointers, but you need to omit symbols such as spaces. Therefore, you should pay attention to the problem that the array is out of bounds when the double pointer moves. At the same time, you should pay attention to the API of two characters: judge whether it is a letter or a number and turn it into lowercase letters
public boolean isPalindrome(String s) {
int n = s.length();
int left = 0, right = n - 1;
while (left < right) {
while (left < right && !Character.isLetterOrDigit(s.charAt(left))) {
++left;
}
while (left < right && !Character.isLetterOrDigit(s.charAt(right))) {
--right;
}
if (left < right) {
if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right))) {
return false;
}
++left;
--right;
}
}
return true;
}Different subsequences
115 questions

Using dynamic programming, dp[i][j] is defined as characters from i-1 to j-1. There are several schemes. When t is an empty string, that is, when j=0, the empty set is a subset of all strings, so it is considered as one. When s is an empty string, dp[0][j]=0 because it cannot match any value except the empty string;
There are only two cases of string matching: 1 is that the characters are equal and 2 is not equal; For this question, when equal, its state can be inherited from the upper left side and the upper side, and when unequal, it can only be inherited from the upper side; It can be understood that when two characters are the same, one character can be removed from the two strings at the same time, so as to inherit the result of the oblique upper corner. In any case, the result obtained by subtracting an s string can be inherited
For example: sasa and sa, when sas and sa are matched, s and a are not equal, so the case of sas and sa is equal to that of sa and sa. When sasa and sa are matched, a==a, it can inherit not only the result 2 of sas==s, but also the result 1 of sas and sa, so there are three kinds in total
| i\j | " " | r | a | b | b | i | t |
| " " | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| r | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| b | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| b | 1 | 1 | 1 | 2 | 1 | 0 | 0 |
| b | 1 | 1 | 1 | 3 | 3 | 0 | 0 |
| i | 1 | 1 | 1 | 3 | 3 | 3 | 0 |
| t | 1 | 1 | 1 | 3 | 3 | 3 | 3 |
public int numDistinct(String s, String t) {
int n1=s.length();
int n2=t.length();
//There are several schemes to represent the first i-1 character of s and the first j-1 character of t
int[][] dp = new int[n1 + 1][n2 + 1];
//When the two characters are equal, dp[i][j]=dp[i-1][j-1]+dp[i-1][j]
//When the two characters are not equal, dp[i][j]=dp[i-1][j]
//base
for (int i = 0; i < n1 + 1; i++) {
dp[i][0]=1;//An empty set is a subset of all strings
}
//You cannot match any string when you are an empty string
for (int i = 1; i < n2 + 1; i++) {
dp[0][i]=0;
}
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if(s.charAt(i-1)==t.charAt(j-1)){
dp[i][j]=dp[i-1][j]+dp[i-1][j-1];
}else{
dp[i][j]=dp[i-1][j];
}
}
}
return dp[n1][n2];
}Maximum path sum of binary tree
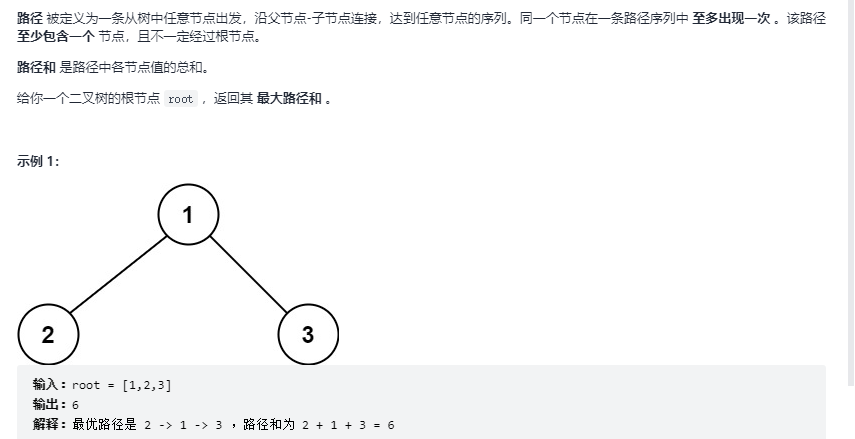
The problem of binary tree needs to distinguish what each node needs to do. Each time it reaches a node, it has three choices for the path. Stop at the node, go to its left child node and go to its right child node
We provide a depth traversal method to return the contribution that the current node can provide to the father; The maximum path provided by a subtree is equal to its own value + the contribution of the left subtree + the contribution of the right subtree; A node can provide the greatest contribution to the parent node, either from the left subtree to itself or from the right subtree to itself. If the contribution is less than 0, it will be discarded directly
int res =Integer.MIN_VALUE;
//Using pre order traversal, there are three choices for each node: stop at the current node, go to the left node and go to the right child node
public int maxPathSum(TreeNode root) {
dfs(root);
return res;
}
private int dfs(TreeNode root) {
if(root==null)return 0;
int left=dfs(root.left);
int right=dfs(root.right);
//The maximum path provided inside a subtree is equal to the maximum path provided by the left subtree and + the maximum path provided by the right subtree and + the current value
res =Math.max(res,root.val+left+right);
//Calculate the maximum contribution that the current node can provide to the father
int max=Math.max(root.val+left,root.val+right);
//If the current contribution is less than 0, discard all directly
return Math.max(max, 0);
}Fill the right pointer of the binary tree
116 - fill the right pointer of the perfect binary tree
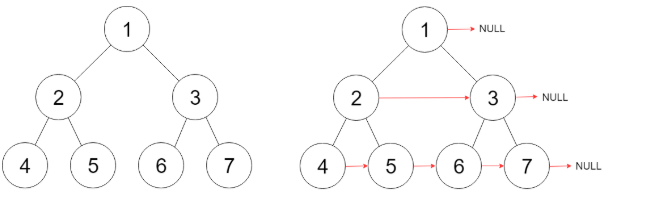
Using depth limited traversal, because it is a perfect binary tree, the condition in the while loop can be a left pointer or a right pointer. For each dfs, it needs to connect its left and right nodes, and then let its left child node move to the right and its right child node move to the left to continue the loop
public Node connect(Node root) {
dfs(root);
return root;
}
private void dfs(Node root) {
if(root==null)return;
Node left=root.left;
Node right=root.right;
while (left!=null){
left.next=right;//The left pointer points to the right pointer
left=left.right;//The left pointer moves to the right
right=right.left;//The right pointer moves to the left
}
//Recursively call left and right nodes
dfs(root.left);
dfs(root.right);
}117 imperfect binary tree filling right pointer
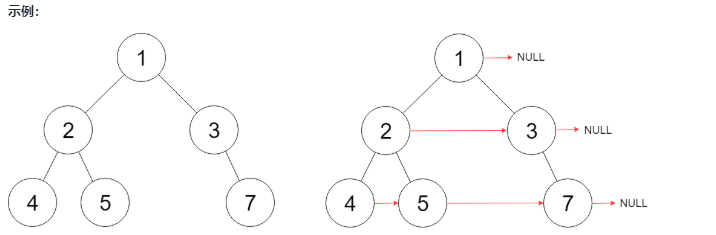
bfs traversal with limited breadth is mainly used here. The framework of bfs is as follows
public void levelOrder(TreeNode tree) {
if (tree == null)
return;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(tree);//It is equivalent to adding data to the end of the queue
while (!queue.isEmpty()) {
//The poll method is equivalent to removing elements from the queue header
TreeNode node = queue.poll();
System.out.println(node.val);
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
}Relying on this framework, it is easy to write the following code to connect each node during sequence traversal
public Node connect(Node root) {
if (root == null)
return root;
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
//Number of each floor
int levelCount = queue.size();
//Previous node
Node pre = null;
for (int i = 0; i < levelCount; i++) {
//Out of the team
Node node = queue.poll();
//If pre is empty, it means that the node node is the first in this line,
//No previous node points to him, otherwise let the previous node point to him
if (pre != null) {
pre.next = node;
}
//Then make the current node the previous node
pre = node;
//If the left and right child nodes are not empty, they will join the team
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
}
return root;
}
The efficiency of the above algorithm is not high. Because the queue is added, it is not necessary to use the queue. You can directly use the next node with the connection number of the previous layer, treat each row as a linked list, and use the linked list of the previous layer to complete the pointer connection of the next row. After completing the connection of the previous layer, cur will be re assigned to the head node of the layer to prepare for the operation of the next row
public Node connect(Node root) {
if (root == null)
return root;
//cur we can think of it as a linked list of each layer
Node cur = root;
while (cur != null) {
//When traversing the current layer, in order to facilitate operation, it is displayed in the next layer
//Add a dummy node in front of the layer (note that this is access
//The nodes of the current layer, and then string the nodes of the next layer)
Node dummy = new Node(0);
//pre indicates the previous node accessing the next layer node
Node pre = dummy;
//Then start traversing the linked list of the current layer
while (cur != null) {
if (cur.left != null) {
//If the left child node of the current node is not empty, let the pre node
//next points to him, that is, string it together
pre.next = cur.left;
//Then update the pre
pre = pre.next;
}
//Similarly, refer to the left subtree
if (cur.right != null) {
pre.next = cur.right;
pre = pre.next;
}
//Continue to the next node in this row
cur = cur.next;
}
//After concatenating the next layer into a linked list, let it assign a value to cur,
//Continue the cycle until cur is empty
cur = dummy.next;//Skip to next line operation
}
return root;
}Sequence traversal of binary tree
It is also called breadth first traversal. Generally, a queue structure is used to help us carry out sequence traversal. Similar questions are 102103107
General sequence traversal
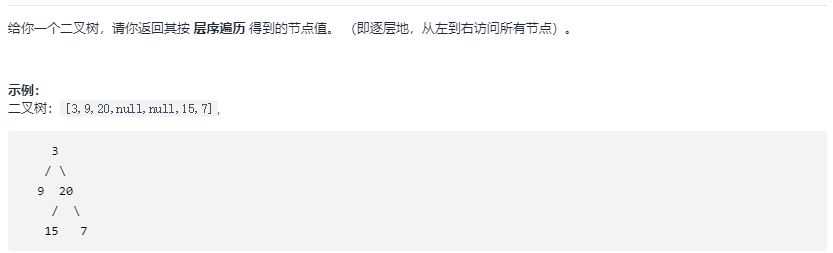
It belongs to the most basic sequence traversal framework. Add the sequence traversal list after the for cycle, and fill the list with data in the for cycle
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res=new ArrayList<>();
//Tools to help us get the hierarchy
ArrayDeque<TreeNode> queue = new ArrayDeque<>();
if(root!=null)queue.add(root);//Add root
while (!queue.isEmpty()){
int n=queue.size();
//Finally, add the list of res
List<Integer> level=new ArrayList<>();
//Dequeue all nodes of the current layer and add the nodes of the next layer to the queue
for (int i = 0; i < n; i++) {
TreeNode node=queue.poll();//Pop up current node
level.add(node.val);//Add all nodes of the current layer
//Join left and right nodes
if(node.left!=null) queue.add(node.left);//The nodes entering the queue for the first time are the nodes of the second layer
if(node.right!=null)queue.add(node.right);
}
res.add(level);
}
return res;
}Zigzag sequence traversal

A variable count is used to determine whether we are currently adding nodes from the tail or from the head
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res=new LinkedList<>();
//Tools to help us get the hierarchy
ArrayDeque<TreeNode> queue = new ArrayDeque<>();
if(root!=null)queue.add(root);//Add root
int count=0;
while (!queue.isEmpty()){
int n=queue.size();
//Finally, add the list of res
LinkedList<Integer> level=new LinkedList<>();
//Dequeue all nodes of the current layer and add the nodes of the next layer to the queue
for (int i = 0; i < n; i++) {
TreeNode node=queue.poll();//Pop up current node
if(count%2==0)level.add(node.val);
else level.addFirst(node.val);
//Join left and right nodes
if(node.left!=null) queue.add(node.left);//The nodes entering the queue for the first time are the nodes of the second layer
if(node.right!=null)queue.add(node.right);
}
count++;
res.add(level);
}
return res;
}Bottom up sequence traversal
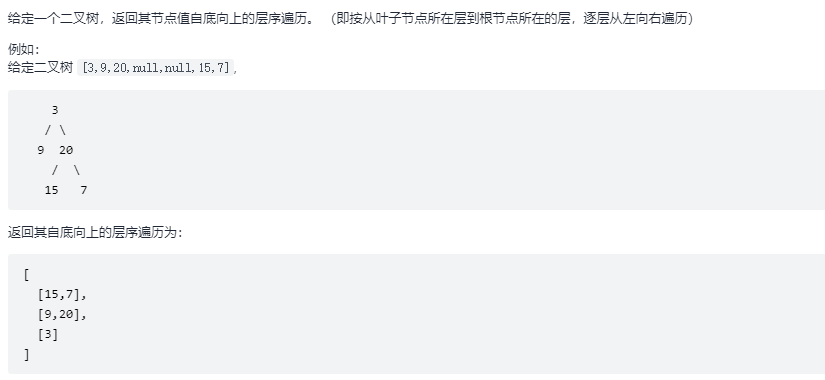
It can be easily solved by using the api of Collections. LinkedList can also be used instead of arraylist for header insertion (arraylist header insertion adds additional overhead)
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> res=new ArrayList<>();
if(root==null)return res;
Deque<TreeNode> deque=new ArrayDeque<>();
deque.addLast(root);
while (!deque.isEmpty()){
int n=deque.size();
ArrayList<Integer> list= new ArrayList<>();
for (int i = 0; i < n; i++) {
TreeNode pop = deque.pop();
list.add(pop.val);
if(pop.left!=null)deque.add(pop.left);
if(pop.right!=null)deque.add(pop.right);
}
res.add(list);
}
Collections.reverse(res);
return res;
}Path summation problem of binary tree
112 and 113
Determine whether there is a path sum
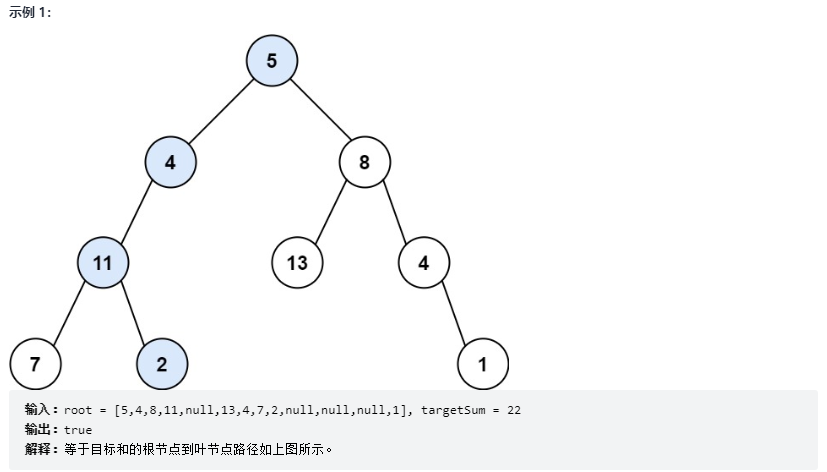
If the termination condition is root==null, it must not succeed at this time. return false directly
For each node, if the node is a leaf node, you need to judge whether its value is consistent with the reduced sum value
If it is not a leaf node, you need to continue looking for results in the left or right subtree
public boolean hasPathSum(TreeNode root, int sum) {
//The last node was not found
if(root == null){
return false;
}
//If it is already a leaf node, check whether the current value is equal to sum
if(root.left == null && root.right == null){
return root.val == sum;
}
//As long as one side on the left and right succeeds
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}Find the path sum
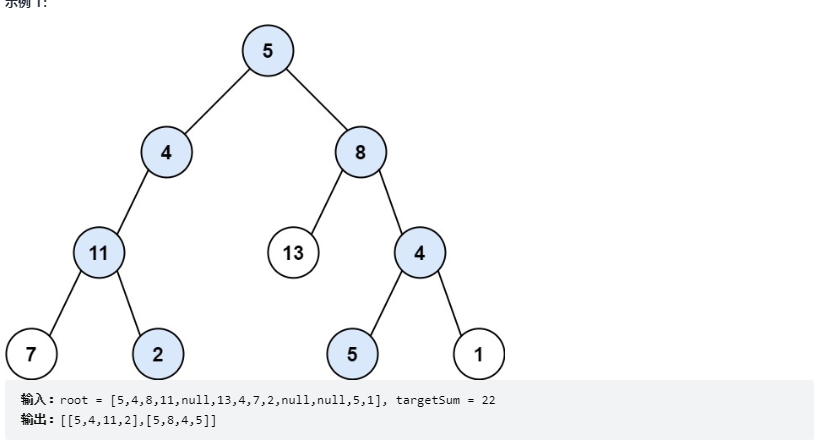
The set requiring specific values is basically done by backtracking algorithm, and the results are added only at the leaf node
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res=new ArrayList<>();
Deque<Integer> path=new ArrayDeque<>();
dfs(root,targetSum,path,res);
return res;
}
private void dfs(TreeNode root, int targetSum, Deque<Integer> path, List<List<Integer>> res) {
if(root==null)return;
path.add(root.val);
if(root.left==null&root.right==null){
if(targetSum==root.val){
res.add(new ArrayList<>(path));
}
}
dfs(root.left,targetSum-root.val,path,res);
dfs(root.right,targetSum-root.val,path,res);
path.removeLast();
}Determine whether it is a balanced binary tree
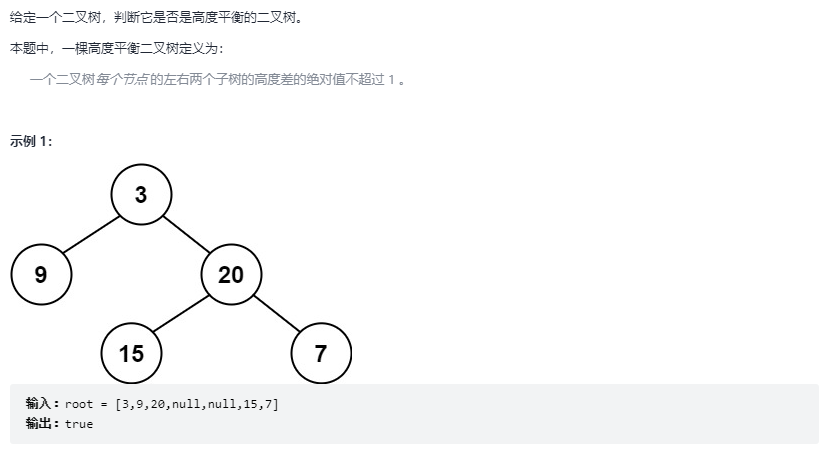
The topic has been very clear. Its definition is that the height difference between two subtrees cannot exceed 1. For each node, it is to calculate the height difference between the left subtree and the right subtree, < = 1 returns true;
This problem uses the postorder traversal method of traversing the left and right roots to make it calculate from bottom to top, because once one does not meet the requirements, it should return - 1 directly, and - 1 will be passed to the last function to make return false
The definition of the height function is to return the height of the modified subtree. As long as the final result is not - 1, it means that the operation has not found that the height difference of the subtree is greater than 1
public boolean isBalanced(TreeNode root) {
return height(root) !=-1;
}
//Postorder traversal from bottom to top
public int height(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = height(root.left);
int rightHeight = height(root.right);
if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
return Math.max(leftHeight, rightHeight) + 1;
}
}Determine whether it is a symmetric binary tree

Using depth first traversal, dfs returns whether the two nodes are symmetrical
public boolean isSymmetric(TreeNode root) {
if(root==null)return true;
return dfs(root.left,root.right);
}
private boolean dfs(TreeNode left, TreeNode right) {
if(left==null&&right==null)return true;
if(left==null||right==null)return false;
if(left.val!=right.val)return false;
return dfs(left.left,right.right)&&dfs(left.right,right.left);
}Binary search tree
Also known as BST tree
Convert an ordered array into a binary search tree
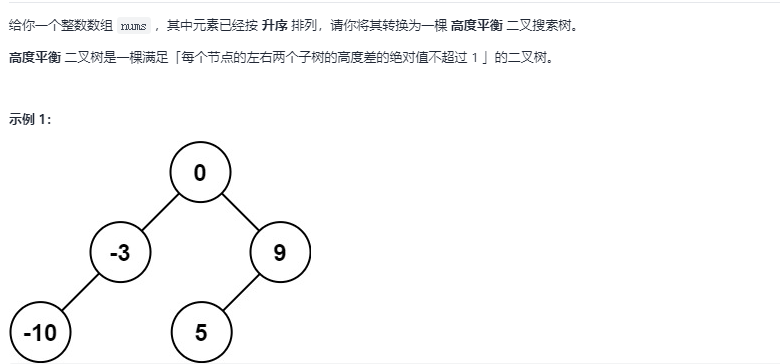
Find the midpoint recursion and build the left subtree and right subtree
public TreeNode sortedArrayToBST(int[] nums) {
return helper(nums,0,nums.length-1);
}
private TreeNode helper(int[] nums, int left, int right) {
if(left>right)return null;
int mid=(left+right)>>1;
TreeNode node = new TreeNode(nums[mid]);
node.left=helper(nums,left,mid-1);
node.right=helper(nums,mid+1,right);
return node;
}Binary search tree with ordered linked list to height balance

Because it is an ordered linked list, the point can be used as the node of the binary search tree, and the fast and slow pointer method is used to find the midpoint of the linked list
In the process of building a binary search tree, let's break the linked list and make it just divided into two parts. If it is an odd linked list, the front will be short and the back will be long, and then recursively call the left child node and the right child node. Because we start from the midpoint, it must be highly balanced
public TreeNode sortedListToBST(ListNode head) {
if(head == null)return null;
if(head.next == null)return new TreeNode(head.val);
//slow points to the current midpoint and pre points to the precursor of the midpoint
ListNode slow = head, fast = head, pre = head;
while(fast != null && fast.next != null){
pre = slow;
slow = slow.next;
fast = fast.next.next;
}
//right points to the successor of the midpoint
ListNode right = slow.next;
//Break the linked list (the core of this problem)
pre.next = null;
TreeNode root = new TreeNode(slow.val);
root.left = sortedListToBST(head);//Build left tree
root.right = sortedListToBST(right);//Build right tree
return root;
}Determine whether it is the same tree
This question is very similar to judging whether it is a symmetric binary tree, except that it is not the left and right nodes, but the following nodes of the two trees
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q == null) return true;
else if (p == null || q == null) return false;
if (p.val != q.val) return false;
return isSameTree(p.right, q.right) && isSameTree(p.left, q.left);
}Determine whether it is a binary search tree
To judge the binary search tree, it is necessary to verify the nature of the binary search tree all the time, whether the root node is larger than the left subtree node and whether the root node is smaller than the right subtree node, and use two variables min and max to record the minimum and maximum values respectively;
For the left node, the root node is the maximum value. The minimum value does not need to be managed and can be directly inherited from the upper function. On the contrary, it is the same for the right node
//Is it a reasonable bst? Since bst requires that all nodes are smaller than the nodes of the right subtree, two nodes min and max are added for comparison
boolean isValidBST(TreeNode node) {
return isValidBST(node, null, null);
}
boolean isValidBST(TreeNode node, TreeNode min, TreeNode max) {
if (node == null) return true;
if (min != null && node.val <= min.val) return false;
if (max != null && node.val >= max.val) return false;
//Compare whether the node on the left is smaller and larger than the current minimum node
return isValidBST(node.left, min, node) && isValidBST(node.right, node, max);
}Check whether a number exists through BST
Find a number. Just find it according to the property that the left is small and the right is large of the binary tree. When root==null, it means that the number does not exist
//Check whether a number exists through BST
boolean isInBST(TreeNode root, int target) {
if (root == null) return false;
if (root.val == target) return true;
if (root.val > target) return isInBST(root.left, target);
else return isInBST(root.right, target);
}Insert a number through BST
The special feature of inserting a number is that you need to find an empty position return, a new node value, and then insert it recursively through the function
//Insert a number through BST
TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) return new TreeNode(val);//Find an empty location and insert a new node
//In general, existing elements are not inserted into BST
if (root.val < val) root.right = insertIntoBST(root.right, val);
if (root.val > val) root.left = insertIntoBST(root.left, val);
return root;
}Delete a number through BST
If this child node is found:
- There are three situations to delete a binary search tree node: if the node
- Both child nodes are empty or have only one child node: directly use this child node to replace its own position
- If the current node has left subtree and right subtree: you need to find the largest left subtree or the smallest right subtree to replace your position
If the current value is greater than the target value, a delete recursive call is made from the left subtree
If the current value is less than the target value, a delete recursive call is made from the right subtree
//Delete a number in BST
TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return null;
if (root.val == key) {
//It happens to be the end node, and both child nodes are empty. If you directly delete this node or have only one non empty child node, you can use it to directly replace your own position
if (root.left == null) return root.right;
if (root.right == null) return root.left;
//If the current node has left subtree and right subtree
TreeNode minNode=getMin(root.right);
root.val=minNode.val;//Switching node
//Delete the node whose value has been replaced
root.right=deleteNode(root.right,minNode.val);
}else if(root.val>key)root.left=deleteNode(root.left,key);
else root.right=deleteNode(root.right,key);
return root;
}
//Get the largest node in the left subtree or the smallest node in the right subtree to replace yourself (here, use the smallest node in the right subtree)
TreeNode getMin(TreeNode node){
while (node.left!=null) node=node.left;
return node;
}Restore binary search tree
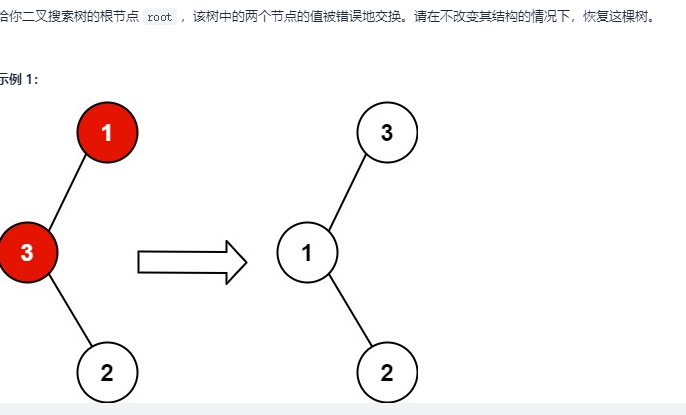
Add the nodes of the binary search tree in the way of medium order traversal. The array of values is arranged in ascending order. The difficulty of this problem is how to determine the two exchanged nodes. Find the x and Y nodes in this way. First find the first node that does not meet the ascending order, locate it in x, then find the last node that does not meet the ascending order, define it as y, and then exchange the position
List<TreeNode> res;
public void recoverTree(TreeNode root) {
res=new ArrayList<>();
helper(root);
TreeNode x=null;
TreeNode y=null;
//Scan the traversal results to find out the nodes x and y that may have wrong node exchange
for (int i = 0; i < res.size() - 1; i++) {
if(res.get(i).val>res.get(i+1).val){
y=res.get(i+1);//Find the last node that does not satisfy ascending order
if(x==null){
x=res.get(i);//Lock the first node that does not satisfy ascending order
}
}
}
//If xy is not empty, exchange two node values
if(x!=null&&y!=null){
int temp=x.val;
x.val=y.val;
y.val=temp;
}
}
private void helper(TreeNode root) {
if(root==null)return;
helper(root.left);
res.add(root);
helper(root.right);
}