The initial brush force deduction starts from the foundation, and the double pointer method is widely used in basic problems.

LeetCode 27, 977, 15 and 18 are the problems I have done in recent days, which can be well solved by double pointer method:

27:

It is equivalent to dividing the array into two parts: the first part is the valid part, which is not equal to the number of Val, and the latter part is the invalid part, which is equal to the number of val. finally, return the length of the previous part, and directly enter the code:

class Solution {
    public int removeElement(int[] nums, int val) {
        int j = nums.length - 1;
        for (int i = 0; i <= j; i++) {
            if (nums[i] == val) {
                swap(nums, i--, j--);
            }
        }
        return j + 1;
    }
    void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

Note the explanation of the stem:

977:

Because the given array is in non incremental order, and the array returned after square is also in non incremental order, that is, the maximum value after square is either at the head and tail of the parameter array. At this point, the idea of double pointers can be used to place a pointer at the head and tail of the array for operation.

There is a clear moving picture in the code Capriccio:

class Solution {
    public int[] sortedSquares(int[] nums) {
        int r=nums.length-1;
        int l=0;
        int []res=new int[r+1];
        int index=res.length-1;//You cannot make index=0 here
        //Because we can only determine that the maximum number after square is at both ends, we must put the result upside down in this way
        while(l<=r)
        {
            if(nums[l]*nums[l] > nums[r]*nums[r])
            {
                res[index--]=nums[l]*nums[l];
                l++;
            }
            else{
                res[index--]=nums[r]*nums[r];
                r--;
            }
        }
        return res;
    }
}

15:

At the beginning, I wanted to use the hash method, but I gave up after trying. It seems that the two finger acupuncture method is more concise:

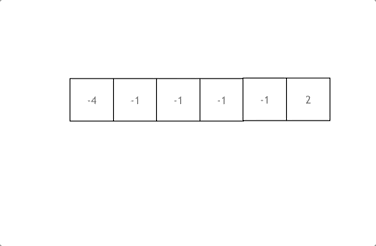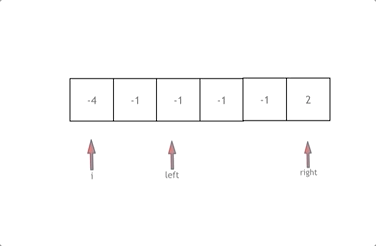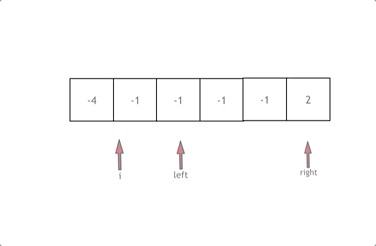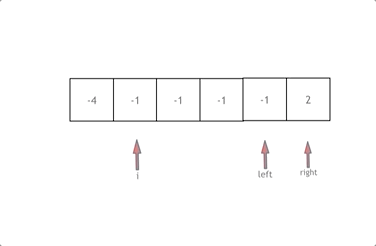
The general idea is: first sort the array, and then loop for. i starts from the subscript 0. At the same time, define a subscript left at the position of i+1 and a subscript right at the end of the array.

When num [left] + num [right] + num [i] > 0, it indicates that the sum of three numbers is too large, and the right subscript should move to the left, so as to make the sum of three numbers smaller< Similarly, move the left subscript at 0.

When num [left] + num [right] + num [i] = 0, it is not all right. Because the number of repeated occurrences cannot be included, further optimization operations are needed.

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List <List<Integer>> result= new ArrayList<>();
        for(int i=0;i<nums.length;i++)
        {
            if (i > 0 && nums[i] == nums[i - 1])
                continue;//Because the answer does not contain repetition, you will jump out of this cycle when you encounter the previously traversed number

            int left=i+1;
            int right=nums.length-1;
            while(left<right)
            {
                int sum=nums[left]+nums[right]+nums[i];
                if(sum>0)
                    right--;
                else if(sum<0)
                    left++;
                //When sum is 0
                else{
                    result.add(Arrays.asList(nums[left],nums[right],nums[i]));
                    while (right > left && nums[right] == nums[right - 1]) right--;
                    while (right > left && nums[left] == nums[left + 1]) left++;
                    //The above is to prevent the inclusion of duplicate figures
                    left++;right--;
                }
            }
        }
        return result;
    }
}

18:

This question is a copy of the previous one. The ideas used are the same:

The double pointer solution of the sum of three numbers is a for loop with num[i] as the determined value, and then there are left and right subscripts in the loop as double pointers. Find num[i] + num [left] + num [right] = = 0.

The double pointer solution of the sum of four numbers is a two-layer for loop. Num [k] + num [i] is the determined value. There are still left and right subscripts in the loop as double pointers. Find out the case where num [k] + num [i] + num [left] + num [right] = = target. The time complexity of the sum of three numbers is O(n2), and the time complexity of the sum of four numbers is O(n3).

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        Arrays.sort(nums);
        List<List<Integer>> result=new ArrayList<>();
        for(int i=0;i<nums.length;i++)
        {
            if(i>0 &&nums[i]==nums[i-1])
                continue;
            for(int j=i+1;j<nums.length;j++)
            {
                if(j>i+1 &&nums[j]==nums[j-1])
                    continue;
                int left=j+1;
                int right=nums.length-1;
                while(left<right)
                {
                    int sum=nums[i]+nums[j]+nums[left]+nums[right];
                    if(sum>target)
                        right--;
                    else if(sum<target)
                        left++;
                    else{                                
                      result.add(Arrays.asList(nums[left],nums[right],nums[i],nums[j]));
                        while(right>left &&nums[right]==nums[right-1]) right--;
                        while(right>left &&nums[left]==nums[left+1]) left++;
                        left++;right--;
                    }
                }
            }
        }
        return result;
    }
}

reference material: Code Capriccio