Summary of dynamic programming of leetcode 3
1 - house raiding
Title Link: Title Link stamp here!!!
Idea: the idea of this question is not difficult, but we need to pay attention to the details.
Recurrence formula: DP [i] = max (DP [I-1], DP [I-2] + num [i])
class Solution {
public int rob(int[] nums) {
if(nums.length==1){
return nums[0] ;
}
if(nums.length==2){
return Math.max(nums[0],nums[1]) ;
}
int [] dp = new int [nums.length] ;
dp[0] = nums[0] ;
dp[1] = Math.max(nums[0],nums[1]) ;
for(int i=2; i<nums.length; i++){
dp[i] = Math.max(dp[i-1], nums[i]+dp[i-2]) ;
}
return dp[nums.length-1];
}
}
2 - house raiding II
Title Link: Title Link stamp here!!!
Idea: the difference between this question and the first question is that the anti-theft system has become a ring, and the recursive formula remains unchanged, except that you can only choose one of the first and last.
class Solution {
public int rob(int[] nums) {
if(nums.length==1){
return nums[0] ;
}
if(nums.length==2){
return Math.max(nums[0],nums[1]) ;
}
return Math.max(f(nums,0,nums.length-1),f(nums,1,nums.length)) ;
}
public int f(int []nums, int begin, int end){
int [] dp = new int [end-begin+1] ;
dp[begin] = nums[begin];
dp[begin+1] = Math.max(nums[begin],nums[begin+1]) ;
for(int i=begin+2; i<end; i++){
dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]) ;
}
return dp[end-1] ;
}
}
3-bit count
Title Link: Title Link stamp here!!!
Idea: the main formula is found recursively, as follows:
dp[2i] = dp[i] ;
dp[2i+1] = dp[i]+1;
class Solution {
public int[] countBits(int n) {
if(n==0){
return new int []{0} ;
}
int [] dp = new int [n+1] ;
dp[0] = 0 ;
dp[1] = 1 ;
for(int i=0; i<=n/2; i++){
dp[2*i] = dp[i] ;
if(2*i+1<=n)
dp[2*i+1] = dp[i]+1;
}
return dp ;
}
}
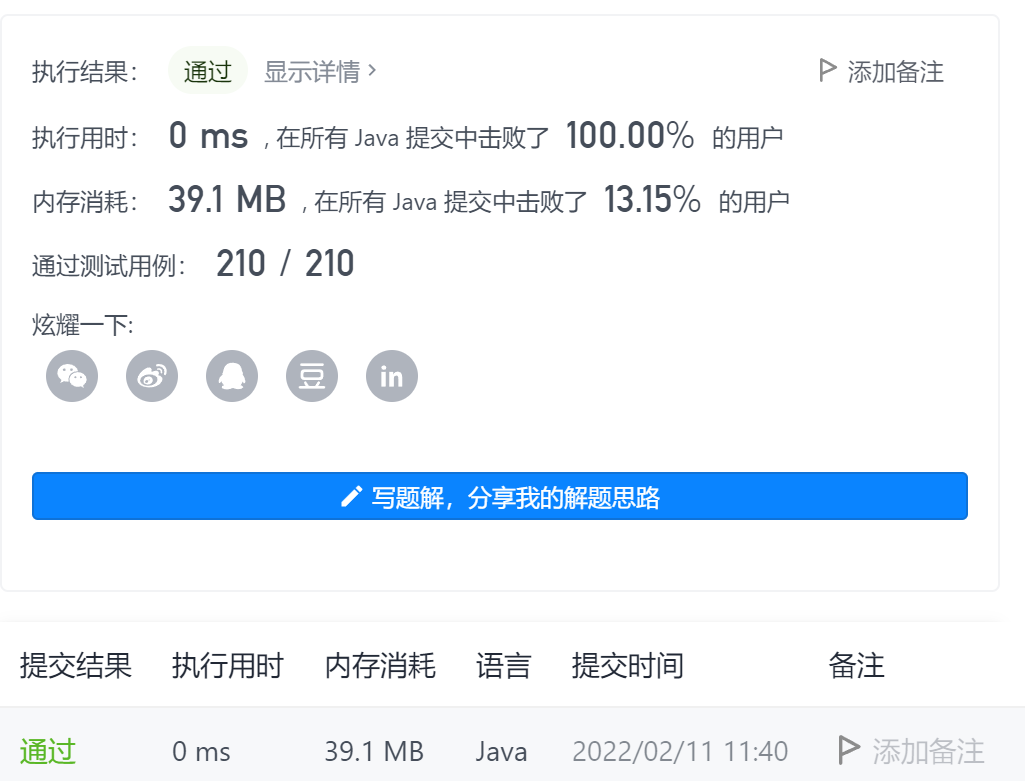
4 - the best stock trading period, including the freezing period
Title Link: Title Link stamp here!!!
Train of thought: sell[i] means that the last operation is the maximum profit at the time of sale as of day I;
buy[i] indicates that as of day I, the last operation is the maximum gain at the time of purchase;
cool[i] refers to the maximum profit when the last operation is the freezing period as of day I;
Recurrence formula:
sell[i] = max(buy[i-1]+prices[i], sell[i-1]) (the first item means selling on day I, and the second item means freezing on day I)
buy[i] = max(cool[i-1]-prices[i], buy[i-1]) (the first item means to buy on day I, and the second item means to freeze on day I)
cool[i] = max(sell[i-1], buy[i-1], cool[i-1])
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==1){
return 0 ;
}
int [] sale = new int [prices.length] ;
int [] buy = new int [prices.length] ;
int [] coll = new int [prices.length] ;
buy[0] = -prices[0] ;
for(int i=1;i<prices.length; i++){
sale[i] = Math.max(sale[i-1],buy[i-1]+prices[i]) ;
buy[i] = Math.max(buy[i-1],coll[i-1]-prices[i]) ;
coll[i] = Math.max(Math.max(coll[i-1],buy[i-1]),sale[i-1]) ;
}
return sale[prices.length-1] ;
}
}
Idea 2:
f[i][0]: represents the maximum profit of holding shares
f[i][1]: represents the maximum profit that does not hold shares but is in the freezing period
f[i][2]: represents the maximum profit that does not hold shares and is not in the freezing period
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==1){
return 0 ;
}
int [][] f = new int [prices.length][3] ;
f[0][0] = -prices[0] ;
for(int i=1;i<prices.length; i++){
f[i][0] = Math.max(f[i-1][0],f[i-1][2]-prices[i]) ;
f[i][1] = f[i-1][0] + prices[i] ;
f[i][2] = Math.max(f[i-1][2],f[i-1][1]) ;
}
return Math.max(f[prices.length-1][1],f[prices.length-1][2]) ;
}
}
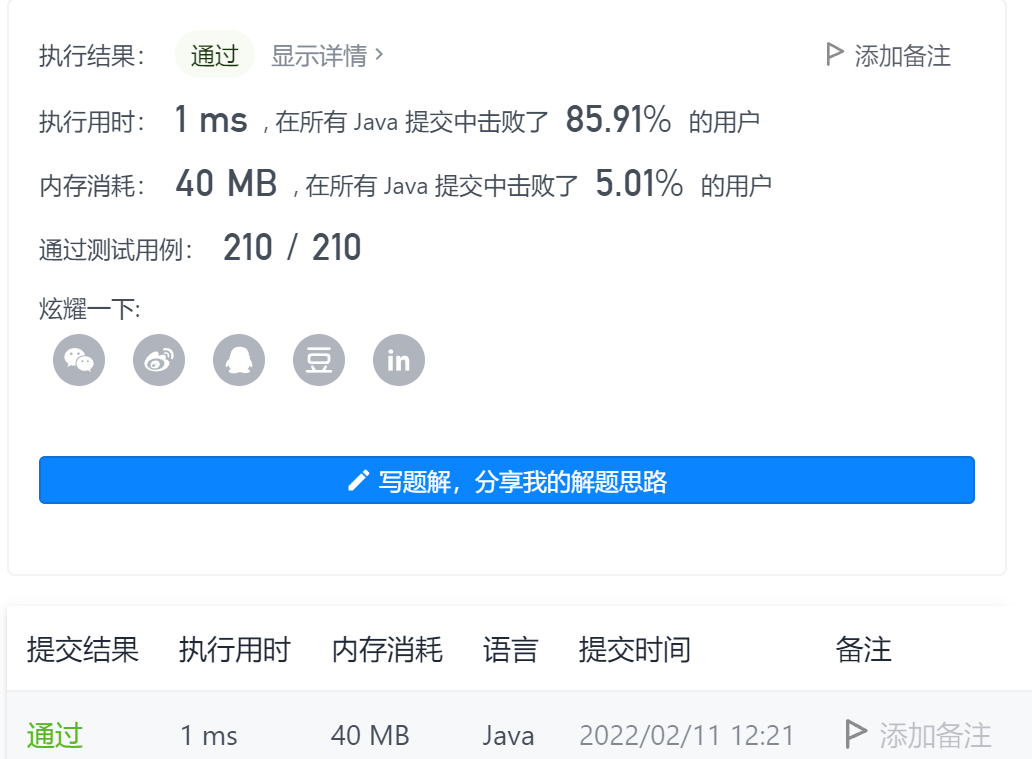
5 - design priority for operation expression
Title Link: Title Link stamp here!!!
Idea: divide and conquer method: if the current string is all numbers, you can return numbers without operation.
Otherwise, you need to find the current symbol, recursively calculate the left half and right half, and then calculate the final result according to the symbol.
class Solution {
public List<Integer> diffWaysToCompute(String expression) {
List<Integer> list = new ArrayList<>() ;
if(isDigits(expression)){
list.add(Integer.parseInt(expression)) ;
return list ;
}
for(int i=0; i<expression.length(); i++){
if(expression.charAt(i)=='+' || expression.charAt(i)=='-' || expression.charAt(i)=='*'){
List<Integer> left = diffWaysToCompute(expression.substring(0,i)) ;
List<Integer> right = diffWaysToCompute(expression.substring(i+1)) ;
char op = expression.charAt(i) ;
for(int j : left){
for(int k : right){
if(op=='+'){
list.add(j+k) ;
}else if(op=='-'){
list.add(j-k) ;
}else if(op=='*'){
list.add(j*k) ;
}
}
}
}
}
return list ;
}
public boolean isDigits(String expression){
for(int i=0; i<expression.length(); i++){
if(!Character.isDigit(expression.charAt(i))){
return false ;
}
}
return true ;
}
}
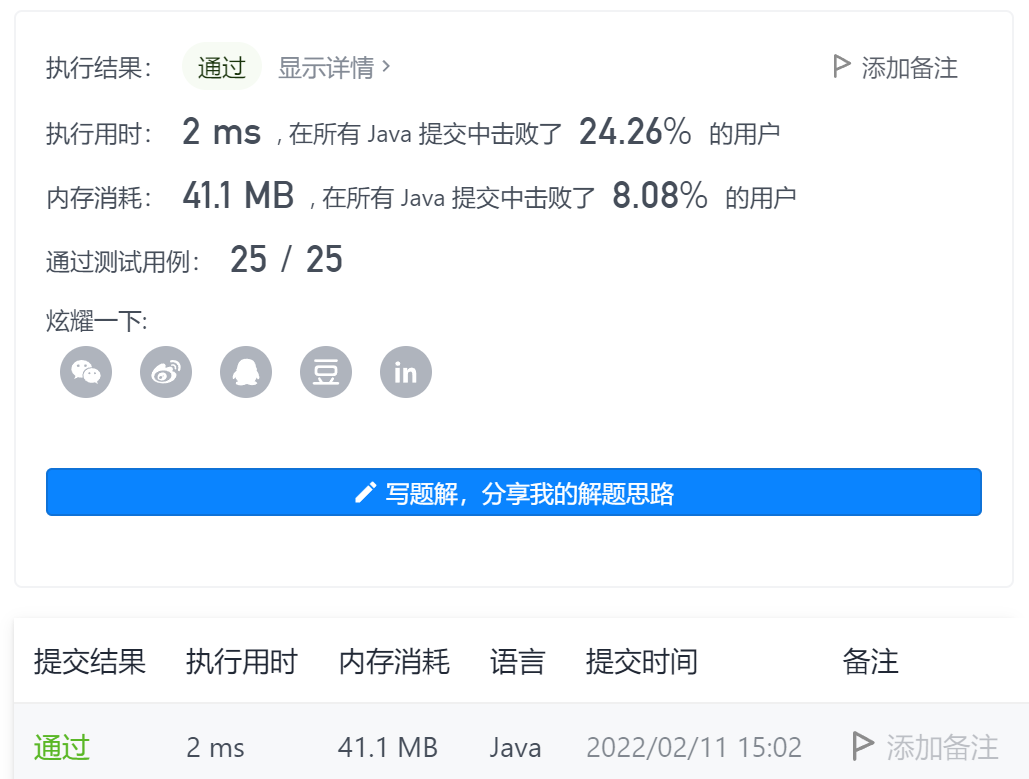
6-integer split
Title Link: Title Link stamp here!!!
Idea: dynamic programming
dp[i]: represents the maximum product of positive integers after splitting positive integer I into the sum of at least two positive integers.
There are two situations:
First, if i is split into i and i-j and i-j does not continue to split, the current value is j*(i-j)
Second, if i is split into i and i-j and i-j continues to split, the current value is j*dp[i-j]
Find out the maximum value of the j-th position in each round.
dp[n] represents the maximum product of positive integers after splitting the positive integer n into the sum of at least two positive integers.
class Solution {
public int integerBreak(int n) {
int [] dp = new int [n+1] ;
for(int i=2; i<=n; i++){
int curMax = 0;
for(int j=1; j<i; j++){
curMax = Math.max(curMax,Math.max(j*(i-j),j*dp[i-j])) ;
}
dp[i] = curMax ;
}
return dp[n] ;
}
}
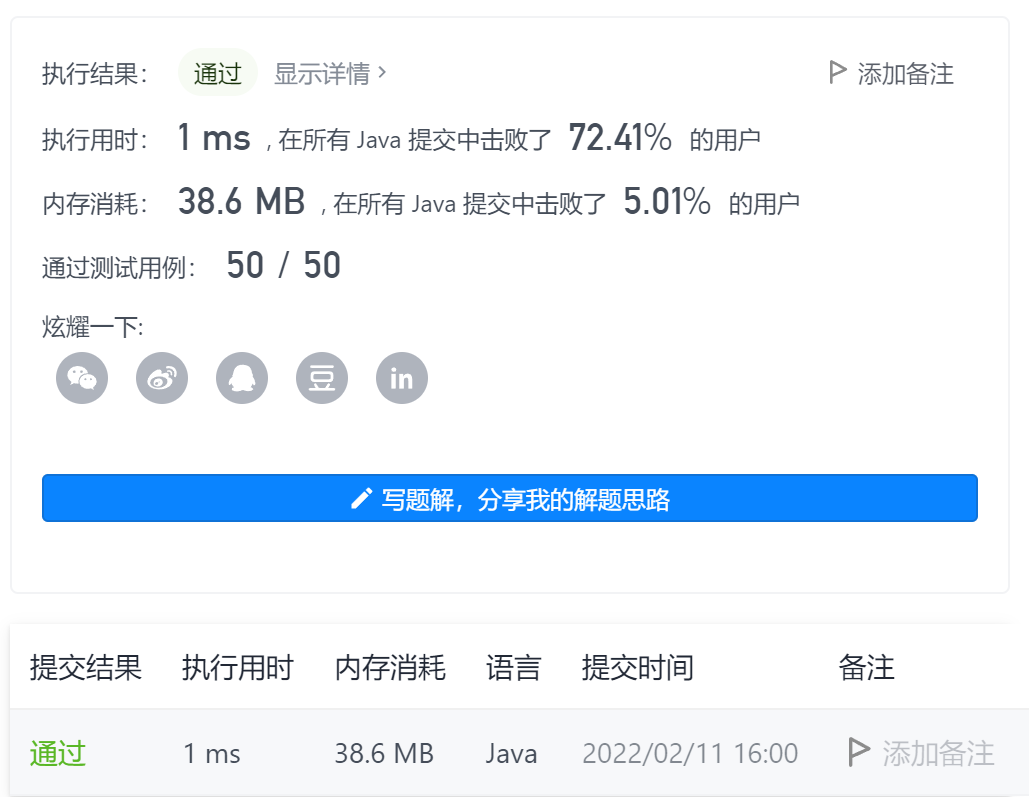
7 - calculate the number of different digits
Title Link: Title Link stamp here!!!
Idea 1: recursive method.
All bits are different
The first 9 choices
There are 9 choices in the second place (because there is one more 0, there are 9 choices in all)
The third place is 8 kinds... And then decrease in turn
How many different numbers of all n digits can be obtained
Add the number of his junior to the returned count
return count+countNumbersWithUniqueDigits(n-1);
class Solution {
public int countNumbersWithUniqueDigits(int n) {
if(n==0){
return 1 ;
}
if(n==1){
return 10 ;
}
int j = 9 ;
int cnt = 9 ;
for(int i=1;i<n; i++){
cnt *= j ;
j -- ;
}
return countNumbersWithUniqueDigits(n-1) + cnt ;
}
}
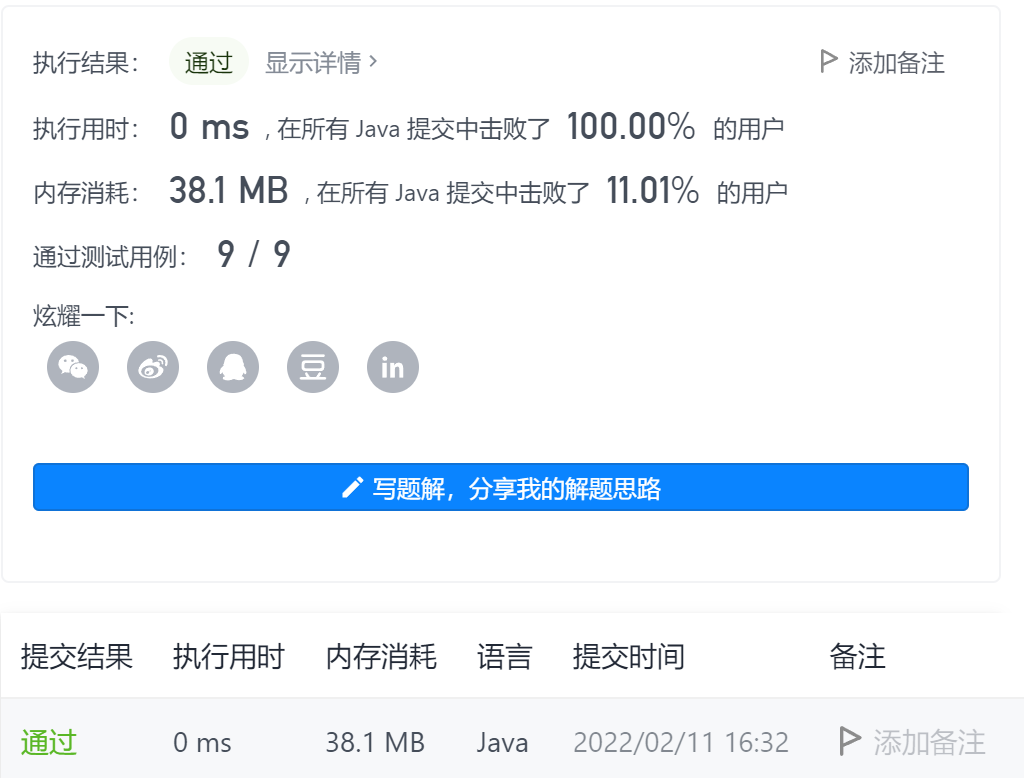
Idea 2: dynamic programming
class Solution {
public int countNumbersWithUniqueDigits(int n) {
if(n==0){
return 1;
}
int [] dp = new int [n+1] ;
dp[0] = 1 ;
dp[1] = 10;
for(int i=2; i<=n; i++){
dp[i] = dp[i-1] + (dp[i-1]-dp[i-2])*(10-(i-1));
}
return dp[n] ;
}
}
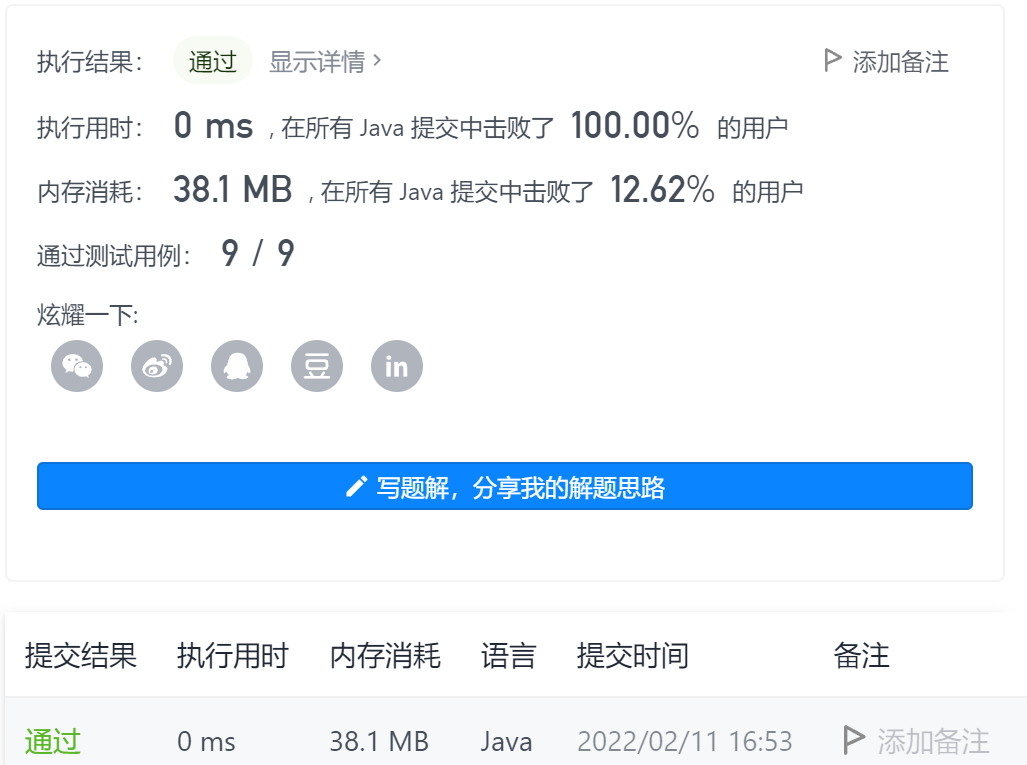
8-judgment subsequence
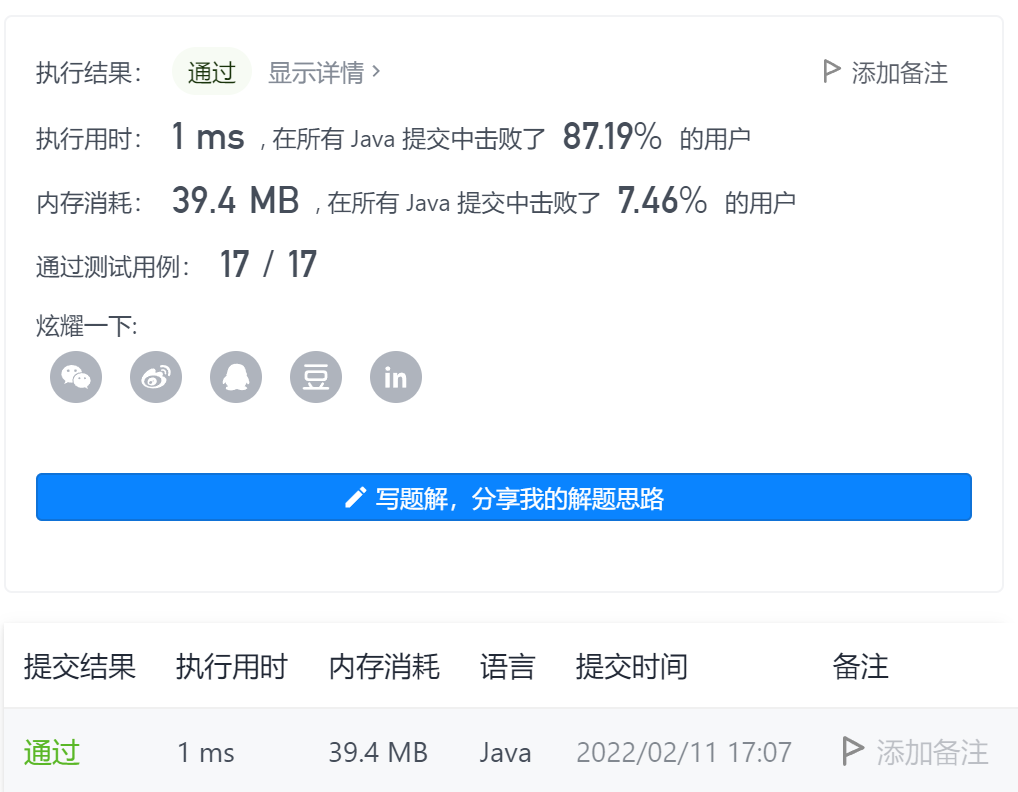
Title Link: Title Link stamp here!!!
Idea 1: Double finger acupuncture.
class Solution {
public boolean isSubsequence(String s, String t) {
int ls = 0, lt = 0 ;
while(ls<s.length() && lt<t.length()){
if(s.charAt(ls)==t.charAt(lt)){
ls ++ ;
}
lt ++ ;
}
return ls==s.length() ;
}
}
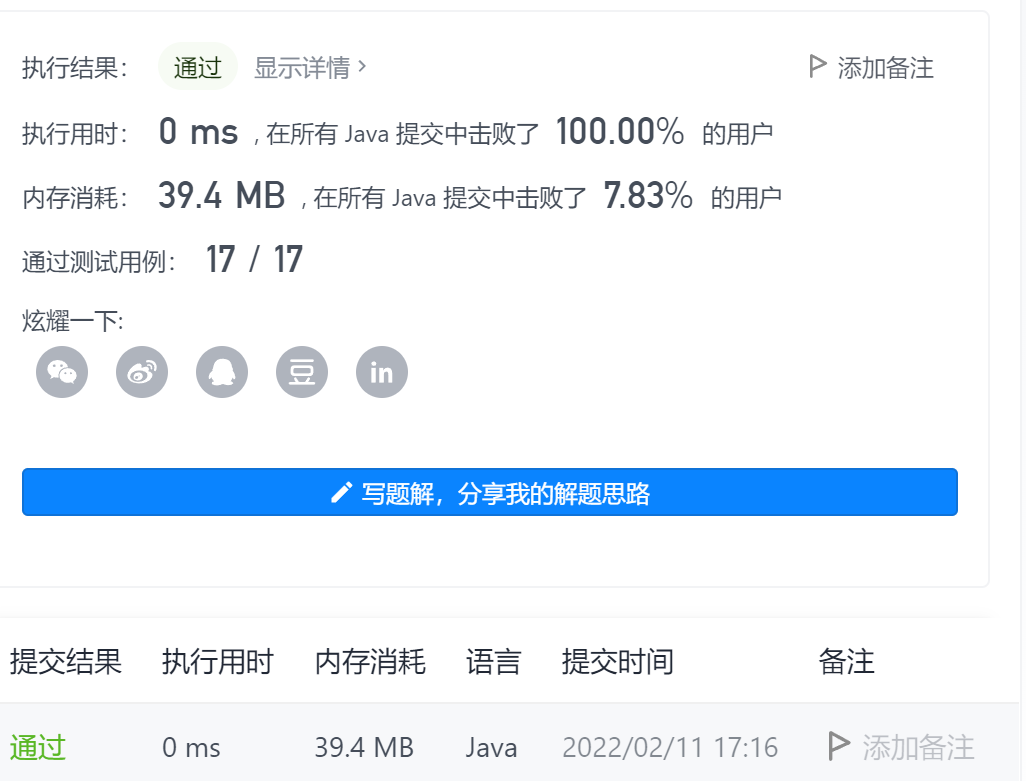
Ha ha, ha ha, ha ha
class Solution {
public boolean isSubsequence(String s, String t) {
int idx = -1 ;
for(char c : s.toCharArray()){
idx = t.indexOf(c,idx+1) ;
if(idx==-1){
return false ;
}
}
return true ;
}
}
9-arithmetic sequence division
Title Link: Title Link stamp here!!!
Idea: regular questions.
This problem mainly needs to find its law. Starting from a small example and observing carefully, we will find that when the whole array is (1, 2, 3, 4, 5, 6), we first take out the first three, (1, 2, 3), the number of equal difference sequences is 1, (1, 2, 3, 4), the number of equal difference sequences is 3, (1, 2, 3, 4, 5), the number of equal difference sequences is 6, and the number of equal difference sequences of (1, 2, 3, 4, 5, 6) is 10, By analogy, we can easily find that adding a number to an arithmetic sequence will add 1 to each increment if it still maintains the characteristics of the arithmetic sequence. If the newly added number does not form an arithmetic sequence with the original sequence, set the increment to 0, then continue the cycle and execute the above logic It can be found that this problem is quite simple as long as we find the law.
class Solution {
public int numberOfArithmeticSlices(int[] nums) {
int add = 0 ;
int res = 0 ;
for(int i=2; i<nums.length; i++){
if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]){
res += (++add) ;
}else{
add = 0 ;
}
}
return res ;
}
}
10-partition and subset
Title Link: Title Link stamp here!!!
If the sum of all the elements in the knapsack is true, it is required to return half of the elements in the knapsack. Otherwise, it is required to return the sum of all the elements in the knapsack, which is equal to 1-false The difference between this problem and the traditional "0-1 knapsack problem" is that the traditional "0 - − 1 knapsack problem" requires that the sum of the weight of the selected items cannot exceed the total capacity of the knapsack. This problem requires that the sum of the selected numbers is exactly equal to half of the sum of the elements of the whole array.
Judge whether the array can be divided according to the length n of the array. If n < 2, it is impossible to split the array into two subsets of elements and equal, so false is returned directly.
Calculate the element sum and maximum element max of the whole array. If sum is an odd number, it is certainly impossible to divide the array into two equal subsets and return false. If the maximum value Max is greater than sum/2, return false
Next, define dp array. dp[i][j] indicates that several positive integers (which can be 0) are selected from the [0,i] subscript range of the array. Whether there is a selection scheme so that the sum of the selected positive integers is equal to j. Initially, all elements in dp are false.
Initialize dp array
dp[i][0]=true
dp[0][nums[0]]=true
The recursive expression is as follows:
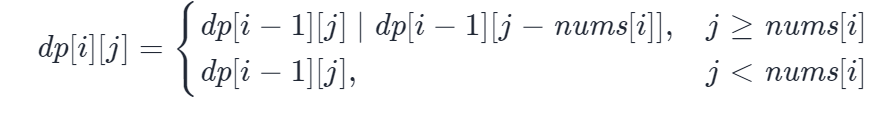
class Solution {
public boolean canPartition(int[] nums) {
int n = nums.length ;
if(n<2){
return false ;
}
int max = 0,sum=0 ;
for(int i=0; i<n; i++){
max = Math.max(max,nums[i]) ;
sum += nums[i] ;
}
int target = sum / 2 ;
if(sum%2!=0 || max>target){
return false ;
}
boolean [][] dp = new boolean [n][target+1] ;
dp[0][nums[0]] = true ;
for(int i=0; i<n; i++){
dp[i][0] = true ;
}
for(int i=1; i<n; i++){
int num = nums[i] ;
for(int j=1; j<=target; j++){
if(j>=num){
dp[i][j] = (dp[i-1][j] | dp[i-1][j-num]) ;
}else{
dp[i][j] = dp[i-1][j] ;
}
}
}
return dp[n-1][target] ;
}
}