It took weeks of intermittent practice and imitation to implement the top ten sorting algorithms using JavaScript code.

There are dynamic and static picture demonstrations of each algorithm. When you see the picture, you can implement it according to the idea of the picture first.

 

The text link in github, Click to see

Two-year front-end learning notes: https://github.com/zhangyachang/Notes Welcome to a star

 

 

Explanation of Sorting Algorithms

1. Bubble Sort 　　1. Algorithmic description   2. Algorithmic Description and Implementation 3. Demonstration of Bubble Sorting Motion Diagram

2. Selection Sort   1. Introduction to Algorithms    2. Algorithmic description and Implementation    3. Select Sort Motion Diagram Demonstration

3. Insertion Sort     1. Brief Introduction of Algorithms     2. Description and Implementation of Algorithms    3. Demonstration of Insert Sort Motion Map

4. sorted sort (Shell Sort)     1. Brief Introduction of Algorithms     2. Algorithmic description and Implementation   3., sort diagram

5. Merge Sort     1. Brief Introduction of Algorithms      2. Algorithmic description and Implementation     3. Demonstration of Merge and Sort Motion Diagram

6. Quick Sort    1. Brief Introduction of Algorithms     2. Algorithmic description and Implementation    3. Demonstration of Quick Sorting Motion Map

7. Heap Sort     1. Brief Introduction of Algorithms     2. Algorithmic description and Implementation     3. Demonstration of Heap Sorting Motion Diagram

8. Counting Sort     1. Brief Introduction of Algorithms     2. Algorithmic description and Implementation    3. Demonstration of Counting and Sorting Motion Diagram

9. Bucket Sort     1. Brief Introduction of Algorithms     2. Algorithmic description and Implementation     3. Barrel Sorting Diagram

Radix Sort     1. Brief Introduction of Algorithms     2. Algorithmic description and Implementation    3. Postscript of Demonstration of Cardinal Sorting Motion Map

 

Explanation of Sorting Algorithms

1. Definition of ranking

Sort a sequence of objects according to a key word

Input: n Numbers: a1,a2,a3,...,an Output: n Numbers Arrangement: a1',a2',a3',...,an', make a1'<=a2'<=a3'<== an'.

The image point is to sit in rows, adjust seats, stand behind high stations, and stand in front of low ones.

2. Explanation of terminology for evaluating algorithms

Stability: if a is in front of B and a=b, A is still in front of B after sorting; instability: if a is in front of B and a=b, a may appear behind B after sorting;

Internal sorting: All sorting operations are done in memory; External sorting: because the data is too large, the data is placed on disk, and sorting can be carried out through data transmission between disk and memory;

Time complexity: The time taken to execute an algorithm. Spatial complexity: The amount of memory required to run a program.

3. Summary of Sorting Algorithms Pictures

 

 

 

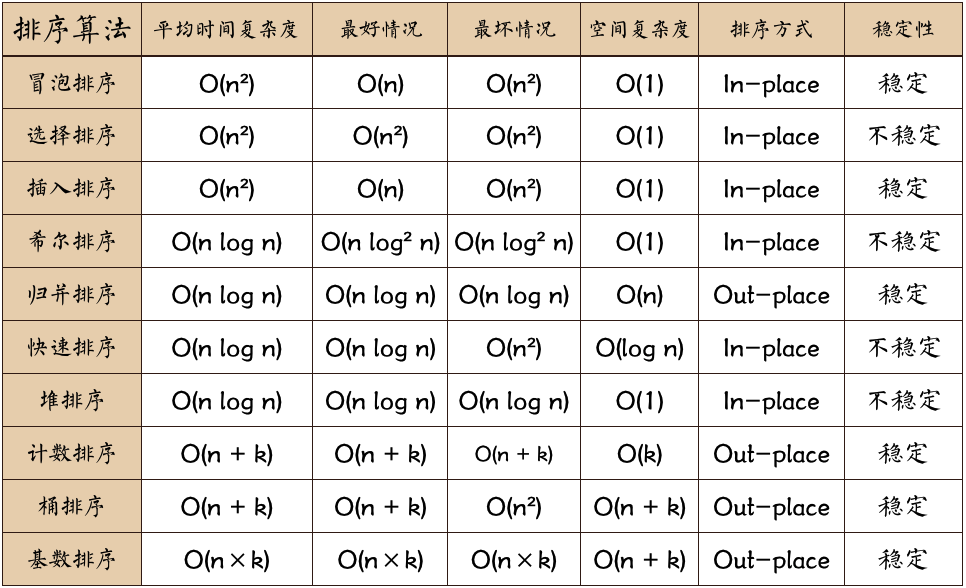
n: Number of k buckets of data size in-place: occupy constant memory, do not occupy extra memory Out-place: occupy additional memory.

 

 

 

1. Bubble Sort

Okay, let's start with the first sorting algorithm, bubble sorting. I think it's the first sort algorithm that many people have come into contact with.

1. Algorithmic Description

Bubble sorting is a simple sorting algorithm. It repeatedly visits the columns to be sorted, compares two elements at a time, and swaps them if their order is wrong. The job of visiting a sequence is to repeat until no exchange is needed, that is to say, the sequence has been sorted. The algorithm's name comes from the fact that smaller elements float slowly to the top of the sequence by swapping.

2. Algorithmic description and Implementation

The specific algorithm is described as follows.

• <1>. Compare adjacent elements. If the first one is bigger than the second one, exchange the two.

• <2>. Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end, so that the last pair of elements should be the largest number.

• Repeat the above operations for all elements except the last one.

• Repeat steps 1-3 until the sorting is complete.

JavaScript code implementation:

function bubbleSort(arr) {
  let len = arr.length;

  for (let i = 0; i < len; i++) {
    for (let j = 0; j < len - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {  // Two-to-two comparison of adjacent elements
        let tmp = arr[j];         // Element exchange
        arr[j] = arr[j + 1];
        arr[j + 1] = tmp;
      }
    }
  }

  return arr;
}

let arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(bubbleSort(arr));
// [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

Improved Bubble Sorting: Set a flag variable post to record the location of the last swap in each sorting. Since the records after the post position have been exchanged in place, it is only necessary to scan to the post position for the next sorting.

The improved algorithm is as follows.

function bubbleSort2(arr) {
  let i = arr.length - 1;
  while (i > 0) {
    let pos = 0;
    for (let j = 0; j < i; j++) {
      if (arr[j] > arr[j + 1]) {
        pos = j; // Record last modification location
        let tmp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = tmp;
      }
    }
    i = pos;
  }
  return arr;
}
​
​
let arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
// let arr = [10, 9, 8, 7, 6, 5, 4, 3, 2, 0, 1];
console.log(bubbleSort2(arr));

In traditional bubble sorting, only one maximum or minimum value can be found in each sorting operation. We consider that two final values (maximum and minimum) can be obtained by using forward and backward bubble twice in each sorting operation, so that the number of lie in sorting can be reduced by almost half.

The improved sorting algorithm is implemented as follows

function bubbleSort3(arr) {
  var low = 0;
  var high = arr.length - 1;
  var tmp, j;
  console.time('2.Improved Bubble Sorting Time-consuming');
  while (low < high) {

    for (j = low; j < high; j++) {
      // Here's the highest order.
      if (arr[j] > arr[j + 1]) { // Forward Bubble, Find the Largest
        tmp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = tmp;
      }
    }
    high--;

    for (j = high; j > low; j--) { // Reverse bubbling to find the smallest
      if (arr[j] < arr[j - 1]) {
        tmp = arr[j];
        arr[j] = arr[j - 1];
        arr[j - 1] = tmp;
      }
    }
    low++;
  }
  console.timeEnd('2.Improved Bubble Sorting Time-consuming');
  return arr;
}


var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(bubbleSort3(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

 

 

 

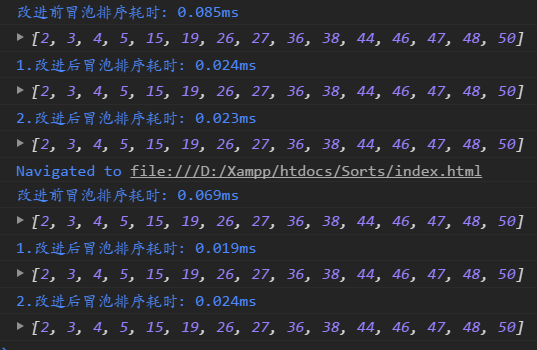
From the graph, it can be seen that the improved bubble sorting obviously has lower time complexity and shorter time-consuming.

3. Demonstration of Bubble Sorting Motion Diagram

 

algorithm analysis

• Best case: T(n) = O(n) When the data of the input value is in positive order (they are all in positive order, why should they be in order for Mao?)

• Worst case: T(n) = O(n2) When the input data is in reverse order (horizontal slot, I directly reverse order is not the end...).

• Average: T(n) = O(n2)

 

2. Selection Sort

One of the most stable sorting algorithms (stability is not stability at algorithm level), because whatever data goes in is the time complexity of O(n). So when using it, the smaller the data, the better. The only advantage may be that it doesn't take up extra memory space. In theory, the choice of sorting is probably the most common sorting method that ordinary people think of.

1. Brief Introduction of Algorithms

Selection-sort is a simple and intuitive sorting algorithm. Its working principle: first, find the smallest (large) element in the unsorted sequence and store it in the starting position of the sorting sequence, then continue searching for the smallest (large) element from the remaining unsorted elements, and then place it at the end of the collating sequence. And so on, until all elements are sorted out.

2. Algorithmic description and Implementation

The direct selection sorting of n records can obtain ordered results through n-1 direct selection sorting. The specific algorithm is described as follows:

• Initial state: the disordered region is R[1,...n], and the ordered region is empty.

• <2>. At the beginning of the first sequence (i=1,2,3,4,...n-1), the current ordered region and the disordered region are R[1.i-1] and R(i.n.) respectively. The row sort selects the record R[k] with the smallest keyword from the current disordered region, and exchanges it with the first record R of the disordered region, so that R[1,...i] and R[i+1...n] become a new ordered region with an increase in the number of records and a new disordered region with a decrease in the number of records, respectively.

• The <3>.n-1 trip ends and the array is ordered.

 

JavaScript Code Implementation

// Selection sort
function selectionSort(arr) {
  var length = arr.length;
  var minIndex, tmp;
  console.time("Selection sort is time-consuming");
  for (var i = 0; i < length - 1; i++) {
    minIndex = i;
    for (var j = i + 1; j < length; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }
    tmp = arr[minIndex];
    arr[minIndex] = arr[i];
    arr[i] = tmp;
  }
  console.timeEnd("Selection sort is time-consuming");
  return arr;
}

var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(selectionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

3. Select Sort Motion Diagram Demonstration

algorithm analysis

• Best case: T(n) = O(n)

• Worst case: T(n) = O(n2)

• Average: T(n) = O(n2)

 

3. Insertion Sort

The insertion sort code implementation is simple and crude without bubble sorting and sorting, but its principle should be the easiest to understand, because anyone who plays poker should be able to understand seconds. Of course, if you say that you never adjust the size of cards when you play poker, you probably won't have any interest in insertion sort algorithms in your life.

1. Brief Introduction of Algorithms

The algorithm description of Insertion-Sort is a simple and intuitive sorting algorithm. It works by constructing ordered sequences for unsorted data, and finding the corresponding positions and inserting them in the ordered sequence from the forward scan. Insertion sort is usually implemented by in-place sorting (that is, sorting only the extra space needed for O(1)). Therefore, in the process of backward forward scanning, a sorting element needs to be repeatedly pushed back to provide the insertion space for the newest elements.

2. Description and Implementation of Algorithms

Generally speaking, insertion sorting is implemented on array by in place. The specific algorithm is described as follows:

• <1>. Starting with the first element, the element can be considered sorted.

• <2>. Remove the next element and scan backwards and forwards in the sorted sequence of elements

• <3>. If the element (sorted) is larger than the new element, move the element to the next location

• Repeat step 3 until you find that the sorted element is less than or equal to the new element.

• After inserting the new element into the location,

• <6>. Repeat steps 2-5

 

JavaScript code implementation:

// This is my implementation. It feels like the code looks so long.
// Insertion sort
function insertionSort(arr) {

  console.log('Print this thing.', Object.prototype.toString.call(arr), Object.prototype.toString.call(arr).slice(8, -1) === 'Array');

  var length = arr.length;
  var tmp;
  console.time('Selection sort is time-consuming');
  for (var i = 0; i < length; i++) {
    let tmp = arr[i];
    for (var j = i; j >= 0; j--) {
      if (j === 0) {
        arr[0] = tmp;
        break;
      }

      if (tmp < arr[j - 1]) {
        arr[j] = arr[j - 1];
      } else {
        arr[j] = tmp;
        break;
      }
    }
  }
  console.timeEnd('Selection sort is time-consuming');
  return arr;
}
// 10 7 8

var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(insertionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

JavaScript Code Implementation

// Insertion sort
function insertionSort(arr) {
  if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array') {
    console.time('Insertion sort is time-consuming');
    for (var i = 1, length = arr.length; i < length; i++) {
      var key = arr[i];
      var j = i - 1;
      while (j >= 0 && arr[j] > key) {
        arr[j + 1] = arr[j];
        j--;
      }
      arr[j + 1] = key;
    }
    console.timeEnd('Insertion sort is time-consuming');
    return arr;
  } else {
    return `array is not an array`;
  }
}
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(insertionSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

Improved insert sorting: Binary lookup for locating insert locations

function binaryInsertionSort(arr) {
  if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array') {
    console.time('Bipartite insertion sort is time-consuming');
    var length = arr.length;
    for (var i = 1; i < length; i++) {

      var left = 0;
      var key = arr[i];
      var right = i - 1;

      while (left <= right) {
        var middle = parseInt((left + right) / 2);
        if (key < arr[middle]) {
          right = middle - 1;
        } else {
          left = middle + 1;
        }
      }

      for (var j = i - 1; j >= left; j--) {
        arr[j + 1] = arr[j]
      }
      arr[left] = key;
    }
    console.timeEnd('Bipartite insertion sort is time-consuming');
    return arr;
  } else {
    throw new Error('arr is not arr');
  }
}

Improvement of comparison before and after

 

 

 

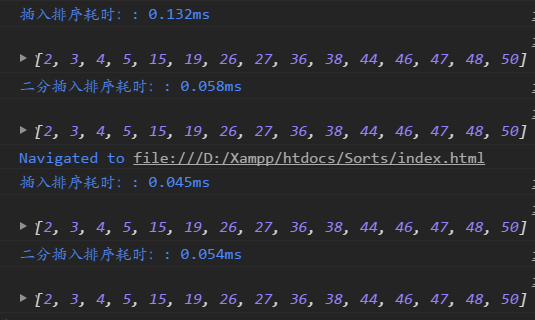
3. Demonstration of Insert Sort Motion Diagram

algorithm analysis

• Best case: Input arrays are sorted in ascending order. T(n) = O(n)

• Worst case: Input arrays are sorted in descending order. T(n) = O(n2)

• Average: T(n) = O(n2)

4. sorted sort (Shell Sort)

Sheel invented in 1959: the first sorting algorithm to break through O(n^2); an improved version of simple insertion sorting; it differs from insertion sorting in that it gives priority to elements farther away. Sorting is also called narrowing incremental sort.

1. Brief Introduction of Algorithms

The core of Hill sorting is the setting of interval sequences. It can not only set the interval sequence in advance, but also dynamically define the interval sequence. The algorithm for dynamically defining interval sequences is proposed by Robert Sedgewick, co-author of Algorithms (4th edition).

2. Algorithmic description and Implementation

Firstly, the whole sequence of records to be sorted is divided into several subsequences for direct insertion and sorting.

• <1>. Select an incremental sequence t1, t2,..., tk, where ti > tj, tk = 1

• <2>. Sequences are sorted k times according to the number of incremental sequences k.

• <3>. In each sorting, according to the corresponding incremental ti, the columns to be sorted are divided into several sub-sequences of length m, and the sub-tables are sorted directly by insertion. When the incremental factor is only 1, the whole sequence is treated as a table, and the length of the table is the length of the whole sequence.

JavaScript Code Implementation

function shellSort(arr) {
  console.log('Called the function method');

  var len = arr.length;
  var tmp;
  var gap = 1;
  console.time('Time consuming');
  while (gap < len / 5) { // Dynamic Definition of Interval Sequences
    gap = gap * 5 + 1;
    console.log('gap -------- ', gap);
  }
    
  // In this case, the insertion and sorting of each group of data is really impossible to write, I don't know. It's easy to think about it once.
    
  for (gap; gap > 0; gap = Math.floor(gap / 5)) {
    console.log('gap ===== >', gap);
    for (var i = 0; i < len; i++) {
      tmp = arr[i];
      for (var j = i - gap; j >= 0 && tmp < arr[j]; j -= gap) {
        arr[j + gap] = arr[j];
      }
      arr[j + gap] = tmp;
    }
  }
  console.timeEnd('Time consuming');
  return arr;
}

var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(shellSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

3., sort diagram

 

algorithm analysis

• Best case: T (n) = O (nlog2n)

• Worst case: T (n) = O (nlog2n)

• Average case: T(n) =O(nlog n)

5. Merge Sort

Like selection sort, merge sort performance is not affected by input data, but it performs much better than selection sort because it is always O(n log n) time complexity. The cost is additional memory space.

1. Brief Introduction of Algorithms

An efficient sorting algorithm based on merge operation is proposed for merge sorting. This algorithm is a very typical application of Divide and Conquer. Merge sort is a stable sort method. By merging the existing subsequences, the complete ordered sequence can be obtained, that is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one ordered table, it becomes a 2-way merge.

2. Algorithmic description and Implementation

The specific algorithm is described as follows:

• The input sequence with length n is divided into two sub-sequences with length n/2.

• The two subsequences were sorted by merging.

• <3>. Combine two sorted subsequences into one final sorting sequence.

JavaScript Code Implementation

// This idea is a bit difficult. It looks like the middle order traversal of the binary tree before.

function mergeSort(arr) { // Using a top-down recursive approach
  // console.log('mergeSort', arr);
  var length = arr.length;
  if (length < 2) {
    return arr;
  }

  var middle = Math.floor(length / 2);
  var left = arr.slice(0, middle);
  var right = arr.slice(middle);
  // console.log('mergeSort', 'left', left, 'right', right);

  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  var result = [];
  console.log('left', left, 'right', right);
  // console.time('merge sort time consuming');
  while (left.length && right.length) {
    if (left[0] <= right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }

  while (left.length) {
    result.push(left.shift());
  }

  while (right.length) {
    result.push(right.shift());
  }
  // console.timeEnd('merge sort time consuming');
  return result;
}


var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(mergeSort(arr));

3. Demonstration of Merge and Sort Motion Diagram

 

Algorithmic analysis:

• Best case: T(n) = O(n)

• Worst case: T(n) = O(nlogn)

• Average case: T(n) = O(nlogn)

 

6. Quick Sort

The name of quick sort is simple and crude, because when you hear the name, you know the meaning of its existence, that is, fast and efficient. It is one of the fastest algorithms to process large data.

1. Brief Introduction of Algorithms

The basic idea of quick sorting is to divide the records into two parts by one-time sorting, in which the keywords of one part of the records are smaller than the keywords of the other part. Then the two parts of the records can be sorted separately to achieve the order of the whole sequence.

2. Algorithmic description and Implementation

Quick sort uses divide and conquer to divide a list into two sub-list s. The specific algorithm is described as follows:

• <1>. Select an element from a sequence called pivot.

• <2>. Reordering sequence, all elements smaller than the benchmark value are placed in the front, and all elements larger than the benchmark value are placed behind the benchmark (the same can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called a Partition operation.

• <3>. recursive sorting ranks the subordinate columns of elements less than the base value and those of elements larger than the base value.

 

JavaScript code implementation:

// The core code of this is written by me, which is somewhat worse than it is. Its core principle is not understood. It is a little different from the following motion picture demonstration. The benchmark he chooses is the one on the right.
// Feeling is not the arrangement.

function quickSort(arr, left, right) {
  if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array' && typeof length === 'number' && typeof right === 'number') {

    // console.log('incoming array', JSON. stringify (arr),'left=>', left,'right==>', right);
    if (left < right) {
      var key = arr[left]; // Starting position
      var setPos = left + 1; // Location of Settings
      var tmp;
      for (var i = left + 1; i <= right; i++) {
        if (arr[i] < key) {
          tmp = arr[i]; // Exchange positions and place less than + 1 next time
          arr[i] = arr[setPos];
          arr[setPos] = tmp;
          setPos++;
        }
      }
      // Exchange key s with pos-1 after the loop completes
      arr[left] = arr[setPos - 1];
      arr[setPos - 1] = key;
      // console.log('every sort','current key value ==>', key,'sort completion current array ==>', JSON. stringify (arr)));

      quickSort(arr, left, setPos - 2);
      quickSort(arr, setPos, right);
      // console.log('arr=======>', arr);
    }
  } else {
    return 'array is not an Array or left or right is not a number!';
  }
  return arr;
}


var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
// var arr = [7, 3, 2, 10, 13, 8, 5];
console.log(quickSort(arr, 0, arr.length - 1));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

 

This algorithm is written without my normal thinking.

function quickSort(array, left, right) {
    console.time('1.Quick sort is time-consuming');
    if (Object.prototype.toString.call(array).slice(8, -1) === 'Array' && typeof left === 'number' && typeof right === 'number') {
        
        if (left < right) {
            var x = array[right], i = left - 1, temp;
            for (var j = left; j <= right; j++) {
                if (array[j] <= x) {
                    i++;
                    temp = array[i];
                    array[i] = array[j];
                    array[j] = temp;
                }
            }
            quickSort(array, left, i - 1);
            quickSort(array, i + 1, right);
        }
        console.timeEnd('1.Quick sort is time-consuming');
        return array;
        
    } else {
        return 'array is not an Array or left or right is not a number!';
    }
}

3. Demonstration of Quick Sorting Motion Map

 

The algorithm looks much simpler.

function quickSort(arr) {
  if (arr.length <= 1) { return arr };
  var pivoIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivoIndex, 1)[0]; // The one who will choose the order will be picked out.
  var left = [];
  var right = [];

  // Put the small one on the left and the big one on the right.
  for (var i = 0, len = arr.length; i < len; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  console.log('left', left, 'right', right);
  return quickSort(left).concat([pivot], quickSort(right));
}

var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
// var arr = [7, 3, 2, 10, 13, 8, 5];
console.log(quickSort(arr));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

 

Algorithmic analysis:

• Best case: T(n) = O(nlogn)

• Worst case: T(n) = O(n2)

• Average case: T(n) = O(nlogn)

 

7. Heap Sort

Heap sorting can be said to be a selective sort that uses the concept of heap to sort.

1. Brief Introduction of Algorithms

HeapSort (HeapSort) is a sort algorithm involved in utilizing the data structure of heap. The heap is a structure of almost complete binary tree, and it satisfies the nature of heap at the same time: that is, the key value or index of the child node is always less than (or greater than) its parent node.

 

2. Algorithmic description and Implementation

The specific algorithm is described as follows.

• <1>. The initial sequence of keywords to be sorted (R1, R2...Rn) is constructed into a large-top heap, which is the initial disordered region.

• Exchange the top element R[1] with the last element R[n], and then a new disordered region [R1,R2,...Rn-1] and a new ordered region (Rn) are obtained, which satisfies R[1, 2... n-1] < R[n];

• Since the new top R[1] may violate the nature of the heap after exchange, it is necessary to adjust the current disordered region (R1, R2...Rn-1) to a new heap, and then exchange R[1] with the last element of the disordered region to obtain a new disordered region (R1, R2...Rn-2) and a new ordered region (Rn-1, Rn). Repeat this process until the number of elements in the ordered region is n-1, then the whole ordering process is completed.

JavaScript code implementation:

/*
  Method description: heap sorting
  @param {Array} arr Array to be sorted
*/

function heapSort(arr) {
  console.log('Heap sort');


  console.log();
  if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array') {

    var heapSize = arr.length;
    var temp;

    console.log('Length of array to be sorted===>', heapSize);


    console.log('Styles of pre-construction stacks', JSON.stringify(arr));
    // Construction reactor
    for (var i = Math.floor(heapSize / 2) - 1; i >= 0; i--) {
      heapify(arr, i, heapSize);
    }
    console.log('Styles after heap initialization is complete', JSON.stringify(arr));

    // Now we need to put the biggest one in the last one, the last one in the first one, reduce the size of the heap one, and slowly put the biggest cycle up.
    console.time('Heap sorting is time-consuming');
    for (var j = heapSize - 1; j >= 1; j--) {
      temp = arr[0];
      arr[0] = arr[j];
      arr[j] = temp;
      heapify(arr, 0, --heapSize);
    }
    console.timeEnd('Heap sorting is time-consuming');
    return arr;
  } else {
    return 'array is not array';
  }
}

/*
  Building Reactors: Maintaining the Nature of Reactors
  @param {Array} arr array
  @param {Number} x Array subscript
  @param {Number} len Heap size
*/
function heapify(arr, x, len) {
  if (Object.prototype.toString.call(arr).slice(8, -1) === 'Array' && typeof x === 'number') {
    var l = 2 * x + 1; // Left subscript
    var r = 2 * x + 2; // Right subscript
    var largest = x; // The default maximum is the parent node
    var temp; // Intermediate Values for Exchange Data Storage

    // Find the maximum in a heap
    if (l < len && arr[l] > arr[largest]) {
      largest = l;
    }
    if (r < len && arr[r] > arr[largest]) {
      largest = r;
    }

    // If the largest is not the parent node, swap locations
    if (largest != x) {
      temp = arr[x];
      arr[x] = arr[largest];
      arr[largest] = temp;
      // Recursive search
      heapify(arr, largest, len);
    }
  } else {
    return 'arr is not an array or x is not a number';
  }
}


var arr = [91, 60, 96, 13, 35, 65, 46, 65, 10, 30, 20, 31, 77, 81, 22];
console.log(heapSort(arr));//[10, 13, 20, 22, 30, 31, 35, 46, 60, 65, 65, 77, 81, 91, 96]

3. Demonstration of Heap Sorting Motion Diagram

 

algorithm analysis

• Best case: T(n) = O(nlogn)

• Worst case: T(n) = O(nlogn)

• Average case: T(n) = O(nlogn)

8. Counting Sort

The core of counting sorting is to convert the input data values into keys and store them in additional open array spaces. As a sort of linear time complexity, counting sort requires that the input data must be an integer with a certain range.

1. Brief Introduction of Algorithms

Counting sort is a stable sorting algorithm. The counting sort uses an additional array C, where the number of elements whose median value of the array A to be sorted equals the number of elements of i. Then the elements in A are arranged in the correct position according to the array C. It can only sort integers.

 

2. Algorithmic description and Implementation

The specific algorithm is described as follows.

• Find the largest and smallest elements in the array to be sorted.

• <2>. The number of occurrences of elements with each value of i in an array is counted and stored in item i of array C.

• <3>. Accumulate all counts (starting with the first element in C, adding each item to the preceding one);

• Fill the target array backwards: Place each element I in item C(i) of the new array, and subtract C(i) by 1 for each element placed.

 

JavaScript Code Implementation

function countingSort(arr) {
  console.log('Counting sort');

  var len = arr.length;
  var B = [];
  var C = [];
  var min = max = arr[0];

  console.time('Counting sort is time-consuming');
  // Initialization Count Sorting
  for (var i = 0; i < len; i++) {
    min = min <= arr[i] ? min : arr[i];
    max = max >= arr[i] ? max : arr[i];
    C[arr[i]] = C[arr[i]] ? C[arr[i]] + 1 : 1;
  }
  console.log('After initialization ends', JSON.stringify(C));
  var k = 0;
  for (var j = min; j < max; j++) {
    C[j + 1] = (C[j + 1] || 0) + (C[j] || 0);
  }

  console.log('After the calculation is completed', JSON.stringify(C));
  console.log('After the calculation is completed arr', JSON.stringify(arr));
  // Now the subscript of C is the value, and the content of C is the number of values.
  debugger;
  for (var k = len - 1; k >= 0; k--) {
    console.log('C[arr[l] - 1]===>', C[arr[k]] - 1, 'arrk===>', arr[k]);
    B[C[arr[k]] - 1] = arr[k];
    C[arr[k]]--;
  }
  console.timeEnd('Counting sort is time-consuming');
  return B;
}
var arr = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];
console.log(countingSort(arr)); //[1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]

 

3. Demonstration of Counting and Sorting Motion Diagram

 

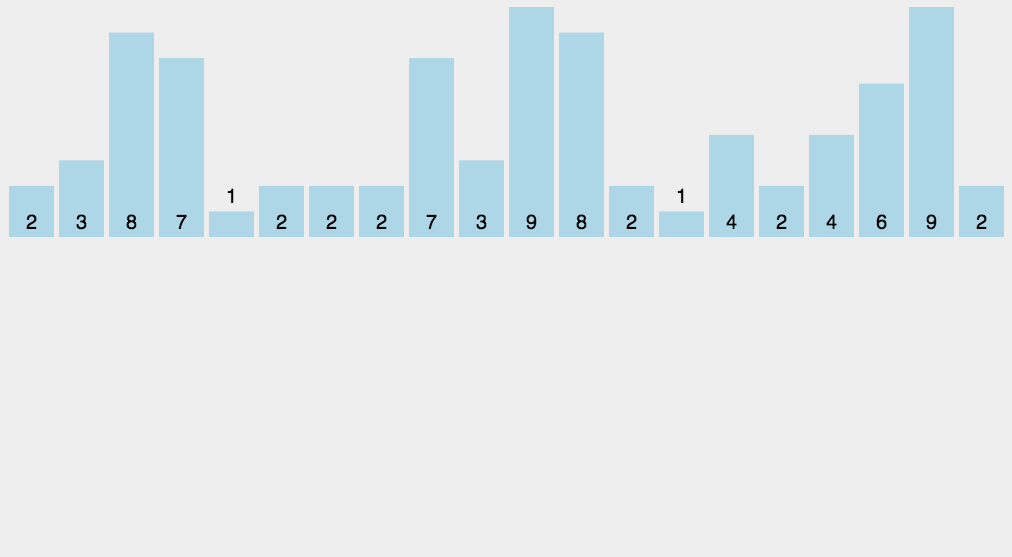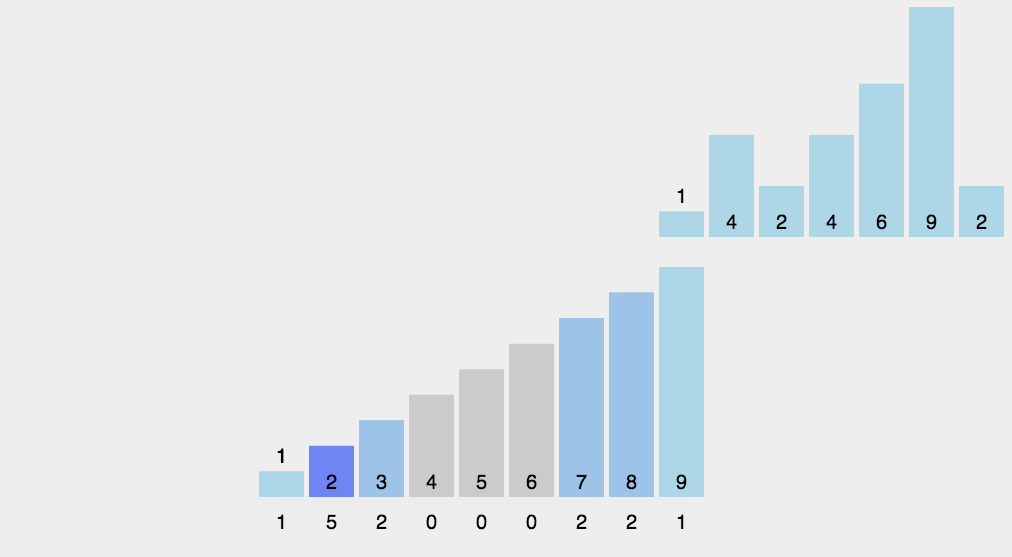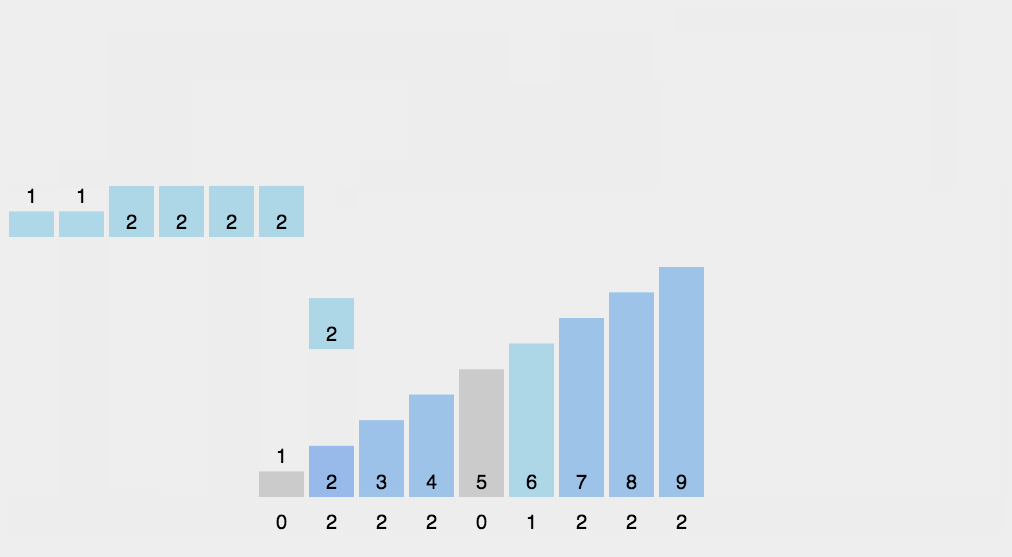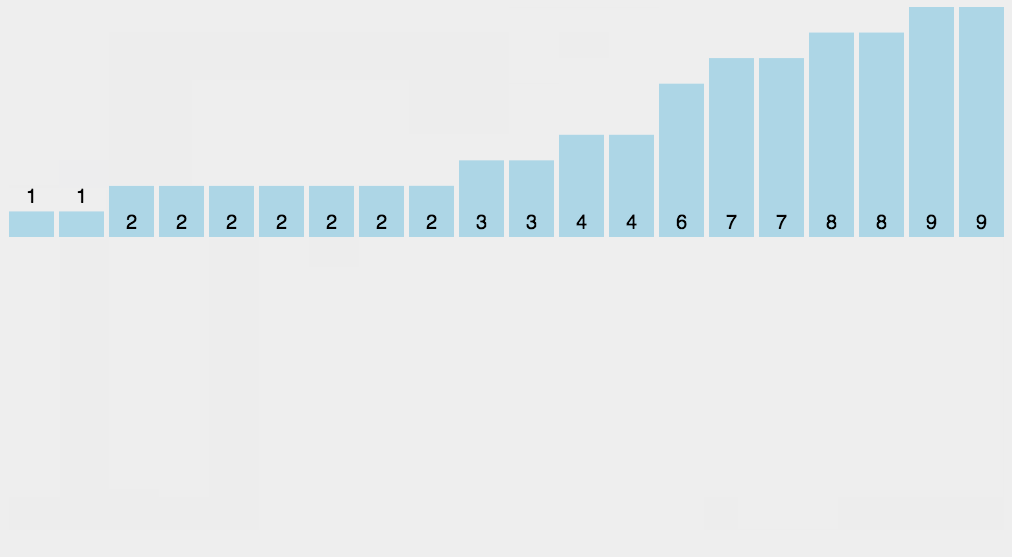
algorithm analysis

When the input element is an integer between N zeros and k, its run time is O(n + k). Counting sorting is not comparative sorting, and the sorting speed is faster than any comparative sorting algorithm. Since the length of the array C used for counting depends on the range of data in the array to be sorted (equal to the difference between the minimum value of the array to be sorted plus 1), counting sort requires a lot of time and memory for arrays with a large range of data.

 

• Best case: T(n) = O(n + k)

• Worst case: T(n) = O(n+k)

• Average case: T(n) = O(n+k)

 

9. Bucket Sort

Bucket sorting is an upgraded version of count sorting. It makes use of the mapping relationship of functions, and the key to its efficiency lies in the determination of the mapping function.

1. Brief Introduction of Algorithms

The working principle of Bucket sort is: assuming that the input data are evenly distributed, the data is divided into a limited number of barrels, and each bucket is sorted separately.

2. Algorithmic description and Implementation

The specific algorithm is described as follows:

• Set up a quantitative array as empty bucket.

• Traverse the input data and put the data one by one in the corresponding bucket.

• Sort each bucket that is not empty.

• <4>. Segmentation of sequenced data from non-empty buckets.

/*
  Method Description: Bucket Sorting
  @param {Array} array
  @param {Number} Quantity of barrels
*/

function bucketSort(arr, num) {
  if (arr.length <= 1) {
    return arr;
  }
  var len = arr.length;
  var buckets = [];
  var result = [];
  var min = max = arr[0];
  var regex = '/^[1-9]+[0-9]*$/';
  var space, n = 0;

  console.log('Sort length ===>', len);

  // Define the number of buckets
  num = num || (num > 1 && regex.test(num) ? num : 10);
  console.log('Bucket sorting is time-consuming');
  // Find the maximum and minimum
  for (var i = 0; i < len; i++) {
    min = (min <= arr[i]) ? min : arr[i];
    max = (max >= arr[i]) ? max : arr[i];
  }
  console.log('Maximum value===> max', max, 'minimum value===> min', min);

  space = (max - min + 1) / num;

  for (var j = 0; j < len; j++) {
    var index = Math.floor((arr[j] - min) / space);
    console.log(`The first ${j}Item value==> ${arr[j]} The index of the bucket is ${index}, space ===> ${space}`);
    if (buckets[index]) { // Non-empty bucket, insert sort
      var key = arr[j];
      var k = buckets[index].length - 1;
      while (k >= 0 && buckets[index][k] > key) {
        buckets[index][k + 1] = buckets[index][k];
        k--;
      }
      buckets[index][k + 1] = key;
    } else { // Empty bucket initialization
      buckets[index] = [];
      buckets[index].push(arr[j]);
    }
  }

  while (n < num) {
    result = result.concat(buckets[n]);
    n++;
  }
  console.log('Bucket sorting completed===>', buckets);
  return result;
}



var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(bucketSort(arr, 4));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

 

/*Method Description: Bucket Sorting
@param  array array
@param  num   Quantity of barrels*/
function bucketSort(array, num) {
    if (array.length <= 1) {
        return array;
    }
    var len = array.length, buckets = [], result = [], min = max = array[0], regex = '/^[1-9]+[0-9]*$/', space, n = 0;
    num = num || ((num > 1 && regex.test(num)) ? num : 10);
    console.time('Bucket sorting time');
    for (var i = 1; i < len; i++) {
        min = min <= array[i] ? min : array[i];
        max = max >= array[i] ? max : array[i];
    }
    space = (max - min + 1) / num;
    for (var j = 0; j < len; j++) {
        var index = Math.floor((array[j] - min) / space);
        if (buckets[index]) {   //  Non-empty bucket, insert sort
            var k = buckets[index].length - 1;
            while (k >= 0 && buckets[index][k] > array[j]) {
                buckets[index][k + 1] = buckets[index][k];
                k--;
            }
            buckets[index][k + 1] = array[j];
        } else {    //Empty bucket, initialization
            buckets[index] = [];
            buckets[index].push(array[j]);
        }
    }
    while (n < num) {
        result = result.concat(buckets[n]);
        n++;
    }
    console.timeEnd('Bucket sorting is time-consuming');
    return result;
}
var arr=[3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
console.log(bucketSort(arr,4));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

 

3. Barrel Sorting Diagram

 

 

algorithm analysis

The linear time O(n) is best used for bucket sorting. The time complexity of bucket sorting depends on the time complexity of sorting data between buckets, because the time complexity of other parts is O(n). Obviously, the smaller the bucket partition, the less data between buckets, and the less time it takes to sort. But the corresponding space consumption will increase.

• Best case: T(n) = O(n + k)

• Worst case: T(n) = O(n + k)

• Average: T(n) = O(n2)

 

Radix Sort

The cardinal sorting is also a non-comparative sorting algorithm. Each bit is sorted from the lowest bit. The complexity is O(kn), which is the length of the array, and k is the largest number of digits in the array.

 

1. Brief Introduction of Algorithms

When cardinality is sorted, it is sorted first according to the low position, then collected; then sorted by the high position, then collected; and then analogized to the highest position. Sometimes some attributes are prioritized, first by low priority, then by high priority. The last order is high priority first, high priority same low priority high priority first. The cardinal sorting is based on sorting separately and collecting separately, so it is stable.

 

2. Algorithmic description and Implementation

The specific algorithm is described as follows:

• Get the maximum number in the array and the number of digits.

• <2>.arr is the original array, and each bit is taken from the lowest bit to form the radix array.

• Count radix (using the characteristics of count sort applicable to small range numbers)

 

JavaScript Code Implementation

/*
  Cardinal sorting is applicable to:
    (1)The data range is relatively small and less than 1000 is recommended.
    (2)Each value should be greater than or equal to 0.
  
  @param {Array} arr Array to be sorted
  @param {Number} Maximum digit
*/
function radixSort(arr, maxDigit) {
  var mod = 10;
  var dev = 1;
  var counter = [];

  console.time('Cardinal sorting is time-consuming');
  for (var i = 0; i < maxDigit; i++ , mod *= 10, dev *= 10) {
    for (var j = 0, len = arr.length; j < len; j++) {
      var bucket = parseInt((arr[j] % mod) / dev);
      console.log('base===>', bucket);
      if (counter[bucket] == null) {
        counter[bucket] = [];
      }
      counter[bucket].push(arr[j]);
    }

    console.log('First Sort Completion===>', counter);
    // Rearrange the sorted items
    var pos = 0;
    for (var j = 0; j < counter.length; j++) {
      console.log('counter[j] ===>', 'j===>', j, counter[j]);
      if (counter[j] != null) {
        while ((value = counter[j].shift()) != null) {
          arr[pos++] = value;
        }
      }
    }
    console.log('First Sort Completion arr ===>', arr);
  }

  console.timeEnd('Cardinal sorting is time-consuming');
  return arr;
}

var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(radixSort(arr, 2)); //[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

 

3. Demonstration of Motion Map of Cardinal Sorting

algorithm analysis

• Best case: T(n) = O(n * k)

• Worst case: T(n) = O(n * k)

• Average: T(n) = O(n * k)

There are two ways to sort cardinality

• MSD Sorts from High

• LSD sort from low

 

Cardinal sorting vs counting sorting vs bucket sorting

All three methods use the concept of barrel, but there are obvious differences in the use of barrel.

1. Cardinal Sorting: Buckets are allocated according to the number of keys per digit.

2. Counting sort: each bucket stores only a single key value

3. Bucket sorting: each bucket stores a range of values

 

Epilogue

I feel that this sentence he said is very good, but also some of my feelings

The top ten sorting algorithms are concluded here. After bloggers concluded, there was only one feeling. Sorting algorithm was extensive and profound, and the algorithm that our predecessors had spent years or even a lifetime trying to figure out is worth our deliberation. Standing at the door of the ten algorithm is still in fear. As a primary school student, the blogger's summing up will inevitably be neglected.

 

 

This article has been referred to. https://github.com/zhangyachang/Sorts Yes, he writes very well.

If you read my article and learn something, I will be very happy.