No reprint!!!
The general activation function has the following properties:

• Nonlinear
  When the activation function is linear, a two-layer neural network can basically approximate all functions. However, if the activation function is an identical activation function, that is, f(x)=x, this property is not satisfied. Moreover, if the MLP uses an identical activation function, the whole network is equivalent to the single-layer neural network;

• Differentiability
  This property is reflected when the optimization method is based on gradient;

• Monotonicity
  When the activation function is monotone, the single-layer network can be guaranteed to be convex;

• f(x)≈x
  When the activation function satisfies this property, if the initialization of parameters is a small random value, the training of neural network will be very efficient; If this property is not satisfied, the initial value needs to be set in detail;

• Range of output values
  When the output value of the activation function is limited, the gradient based optimization method will be more stable, because the representation of features is more significantly affected by the limited weight; When the output of the activation function is infinite, the training of the model will be more efficient, but in this case, a smaller Learning Rate is generally required

Now let's introduce the current activation function:

Sigmoid function

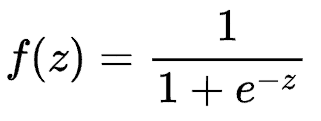
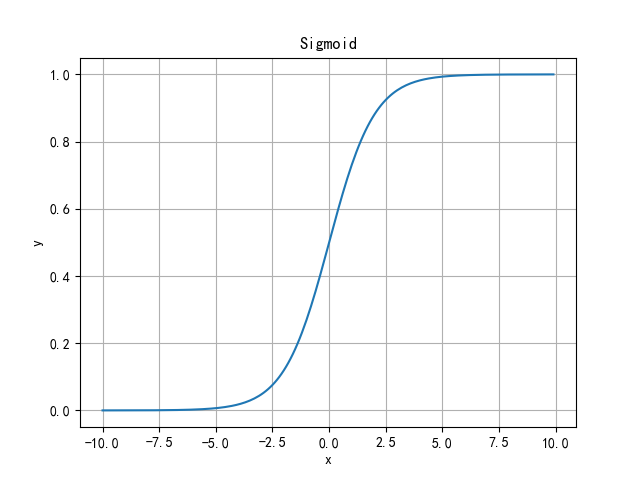
Features: it can transform the continuous real value of the input into the output between 0 and 1. In particular, if it is a very large negative number, the output is 0; If it is a very large positive number, the output is 1.
Disadvantages: the gradient disappears when the gradient is transferred backward in the depth neural network. The output of Sigmoid is not zero centered, which will cause the neurons in the latter layer to get the non-zero mean signal output from the upper layer as the input. Its analytic formula contains power operation, which will increase the training time.

H-Sigmoid function

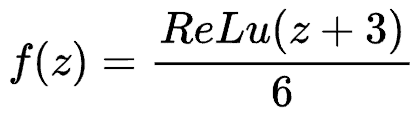
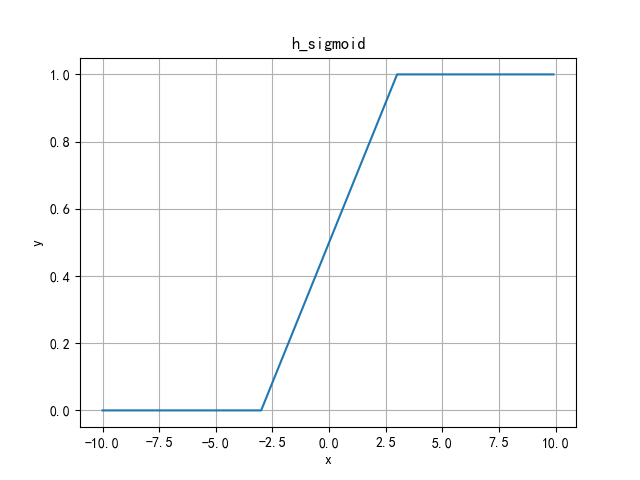
Since the exponential calculation of sigmoid function is particularly time-consuming, ReLU6*(x+3)/6 is used to approximate the substitution.

Tanh function

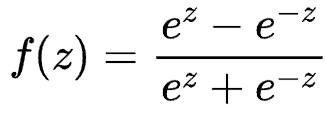
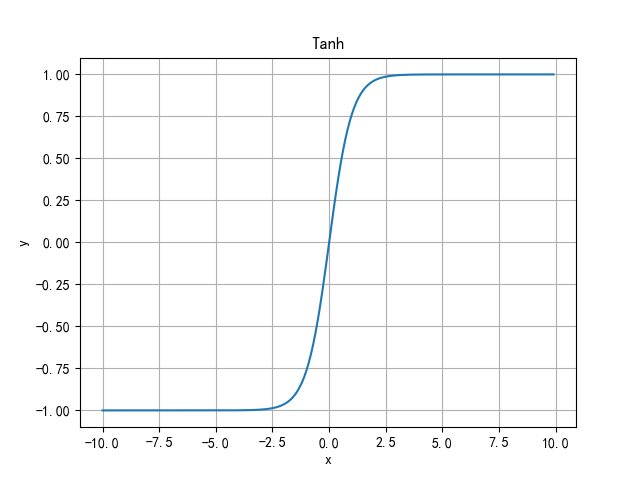
It solves the problem of non-zero centered output of Sigmoid function. However, the problem of gradient disappearance and power operation still exist.

ReLu function

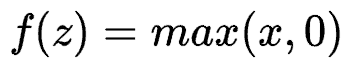
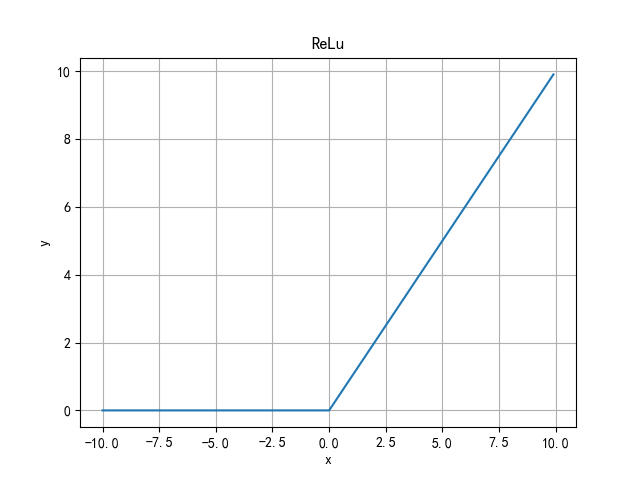
Advantages: when the input is positive, there is no gradient saturation problem. The calculation is much faster.
Disadvantages: neuron inactivation problem. When the input is negative, ReLU will completely fail. In the process of back propagation, if a negative number is input, the gradient will be completely zero. The ReLU function is also not a 0-centered function. The forward output is infinite. Function derivation is discontinuous.

Softplus function

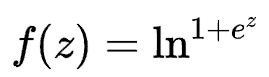
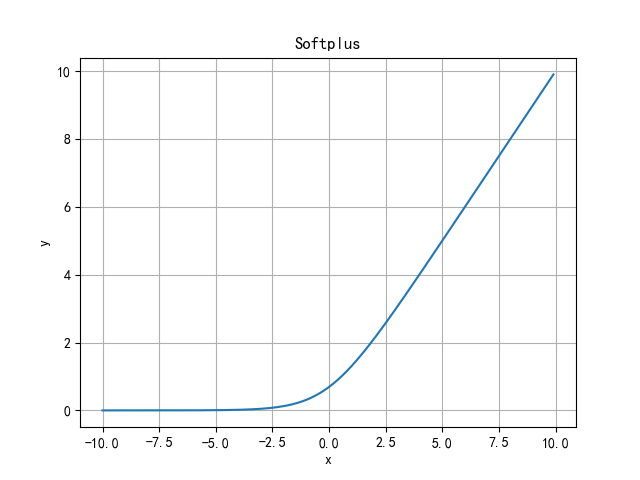
Softplus function can be regarded as the smoothing of ReLU function.

Leaky ReLu function

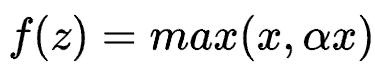
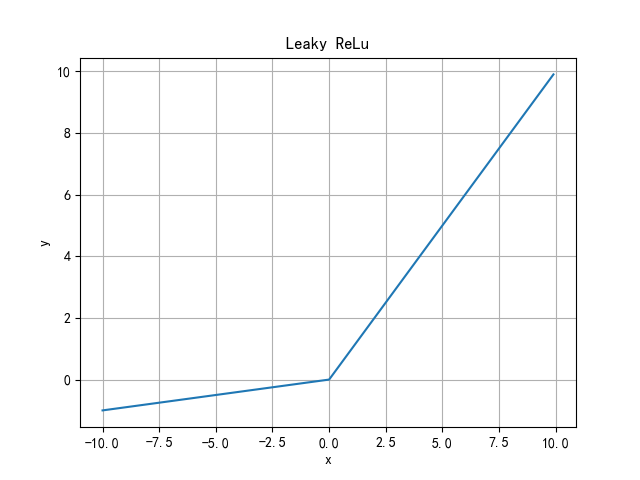
Leaky ReLU function adjusts the zero gradient (neuron inactivation) problem of negative value by giving a very small linear component to negative input. Helps to expand the scope of the ReLU function, usually α The value of is about 0.01. However, the forward output is still infinite. Function derivation is discontinuous.

PReLu(Parametric) function

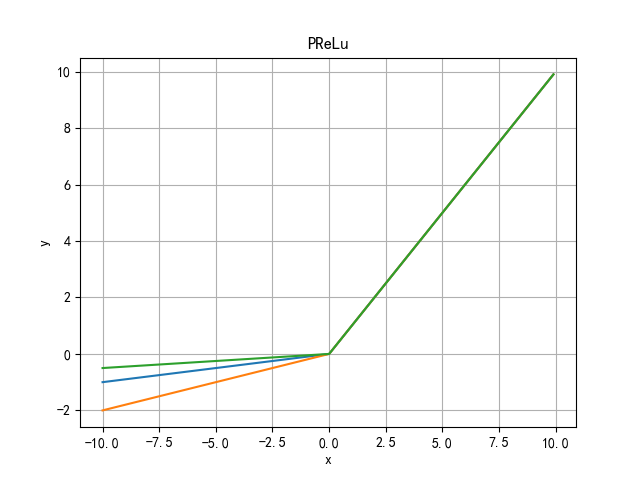
α Can learn

Randomized Leaky ReLu function

Randomized Leaky ReLU is a random version of Leaky ReLU( α Is a random selection). It was first proposed in the NDSB competition. The core idea is that in the process of training, α It is randomly selected from a Gaussian distribution N, and then corrected during the test (similar to the usage of Dropout). In the testing phase, all the α i take an average. NDSB champion α It is randomly selected from N(3,8).

ELU(Exponential Linear Units) function

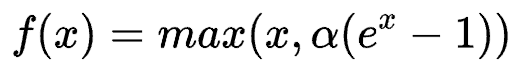
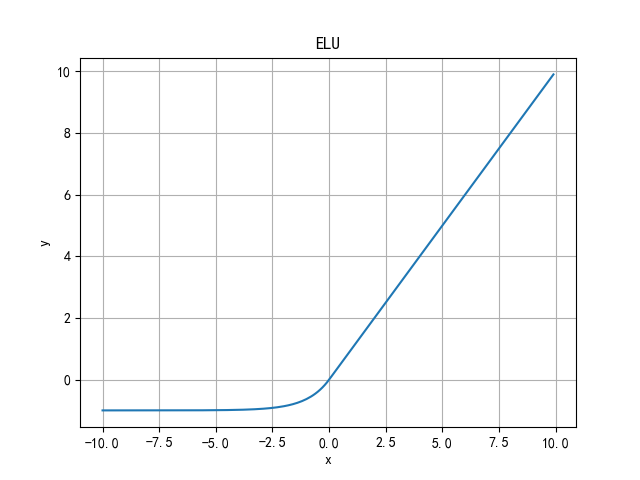
The calculation intensity of the ELU function is higher. Similar to Leaky ReLU, although it is better than ReLU in theory, there is no sufficient evidence in practice that ELU is always better than ReLU.

ReLu6 function

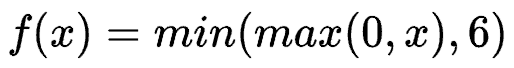
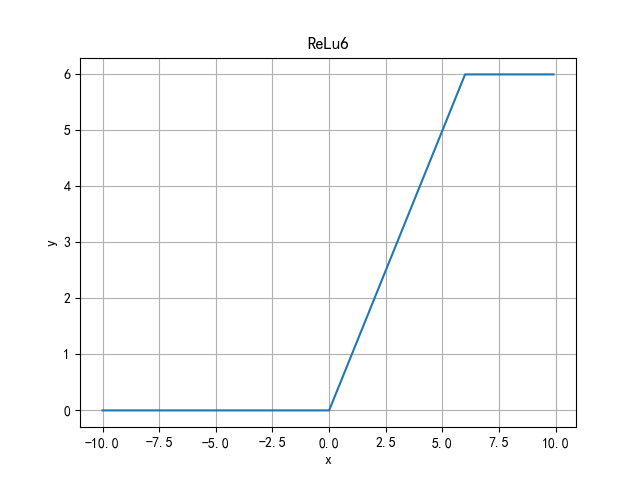
Limit the maximum value to 6 to solve the problem that the forward output of ReLu is infinite.

Swish function (SiLU)

Sigmoid Weighted Liner Unit(SiLU)

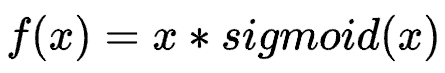
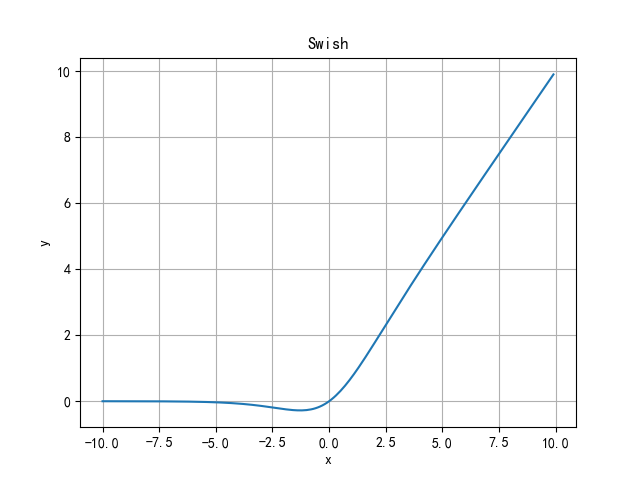
Swish's design is inspired by the use of the sigmoid function of gating. Sigmoid here is used as the automatic control door.

H-Swish function

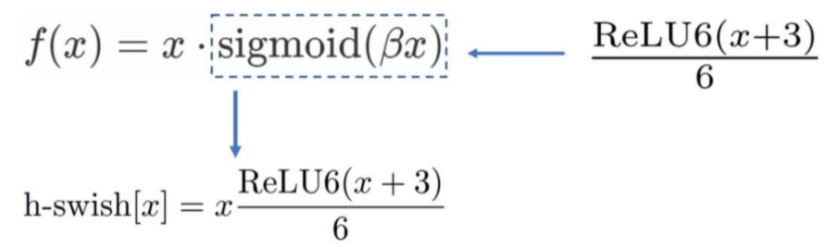
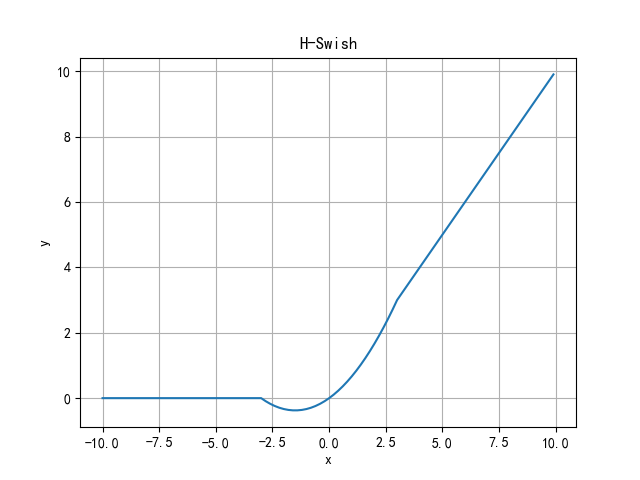
H-Swish as for Lightweight network The activation function appears in the ICCV 2019 published by Google MobileNet V3 Yes. In the Swish function, because the exponential calculation of sigmoid function is particularly time-consuming, it is not suitable for the network deployed on the mobile end. The author uses ReLU6*(x+3)/6 to approximately replace sigmoid and named it h-sigmoid.

Mish function

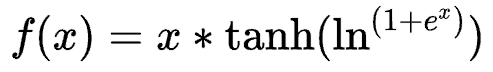
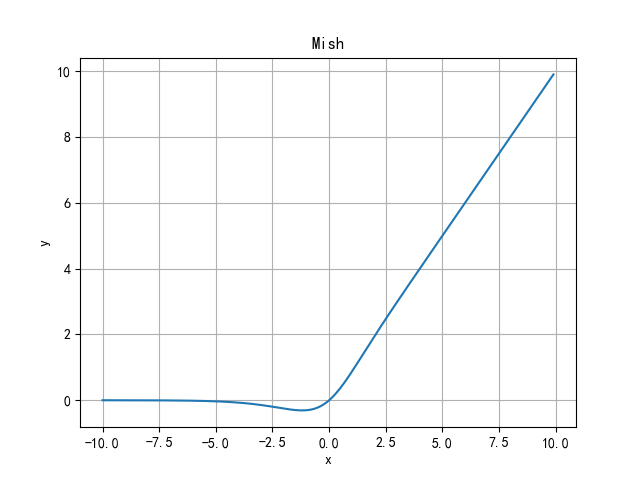
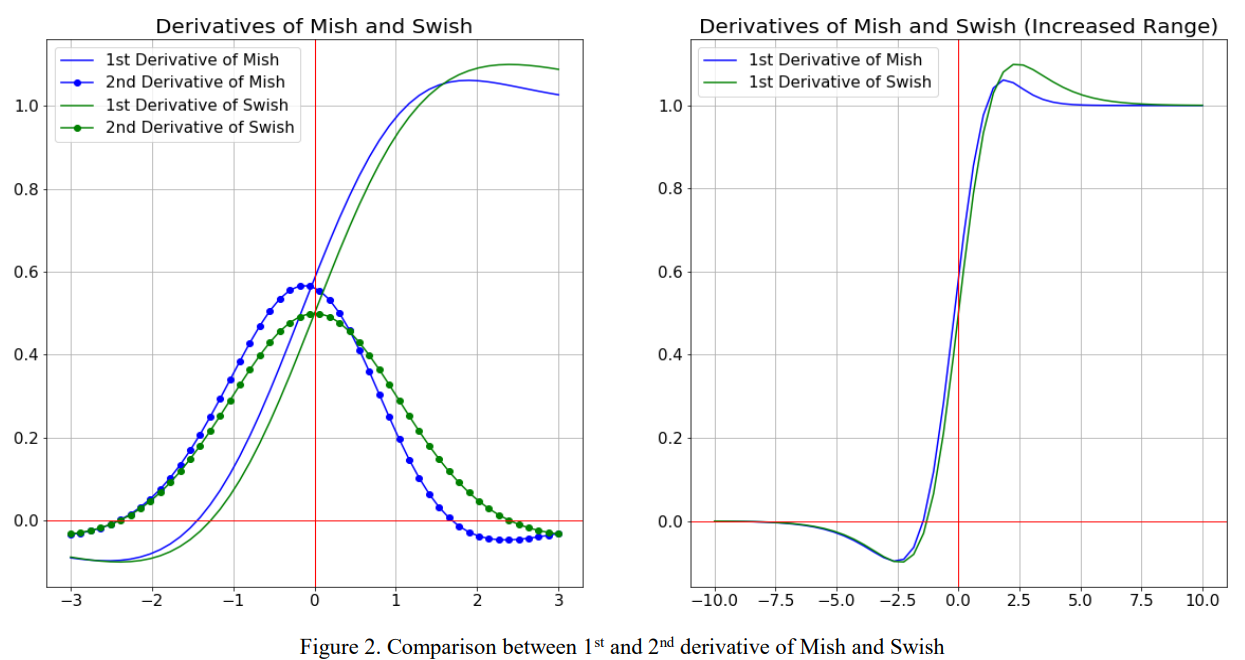
• No upper bound and lower bound: no upper bound is a characteristic required by any activation function, because it avoids gradient saturation that leads to a sharp decline in training speed. Therefore, speed up the training process. The lower bound attribute helps to achieve strong regularization effect (appropriate fitting model). (this property of Mish is similar to that of ReLU and Swish, and its range is [≈ 0.31, ∞).
• Nonmonotonic function: this property helps to maintain a small negative value, so as to stabilize the gradient flow of the network. Most commonly used activation functions cannot maintain negative values, so most neurons are not updated.
• Infinite order continuity and smoothness: Mish is a smooth function with good generalization ability and effective optimization ability of results, which can improve the quality of results. However, Swish and Mish are more or less similar in macro view.

class Mish(nn.Module):
    @staticmethod
    def forward(x):
        return x * F.softplus(x).tanh()


class MemoryEfficientMish(nn.Module):
    class F(torch.autograd.Function):
        @staticmethod
        def forward(ctx, x):
            ctx.save_for_backward(x)
            return x.mul(torch.tanh(F.softplus(x)))  # x * tanh(ln(1 + exp(x)))

        @staticmethod
        def backward(ctx, grad_output):
            x = ctx.saved_tensors[0]
            sx = torch.sigmoid(x)
            fx = F.softplus(x).tanh()
            return grad_output * (fx + x * sx * (1 - fx * fx))

    def forward(self, x):
        return self.F.apply(x)

Gaussian error linear element (GELUs)

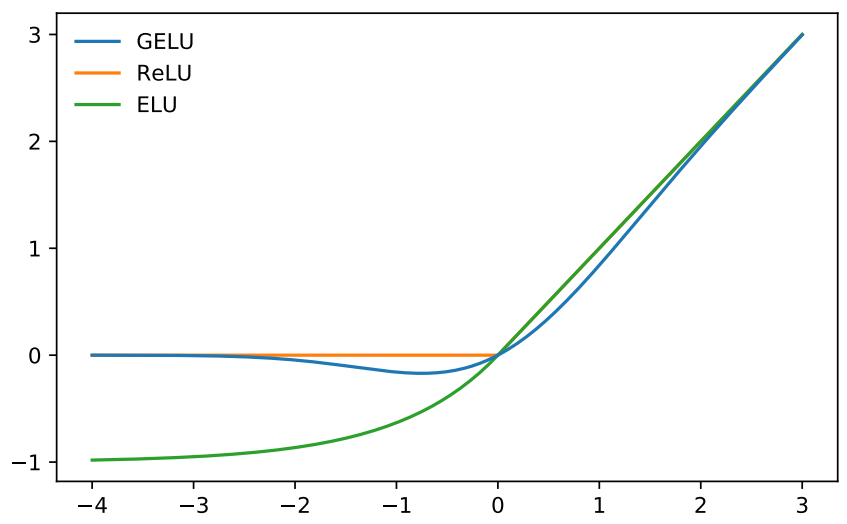
The important property of the model is nonlinearity. At the same time, for the generalization ability of the model, random regularization needs to be added, such as dropout (in fact, it is also a disguised random nonlinear activation).

Gaussian error linear element GELU The idea of stochastic regularity is introduced into activation, which is a probabilistic description of neuronal input. The cumulative distribution function of Gaussian distribution is to integrate the Gaussian function from left to right, and you will get an S-shaped curve.

Gaussian error linear unit activation function has been applied in recent Transformer models, including Google's BERT and OpenAI's GPT-2.

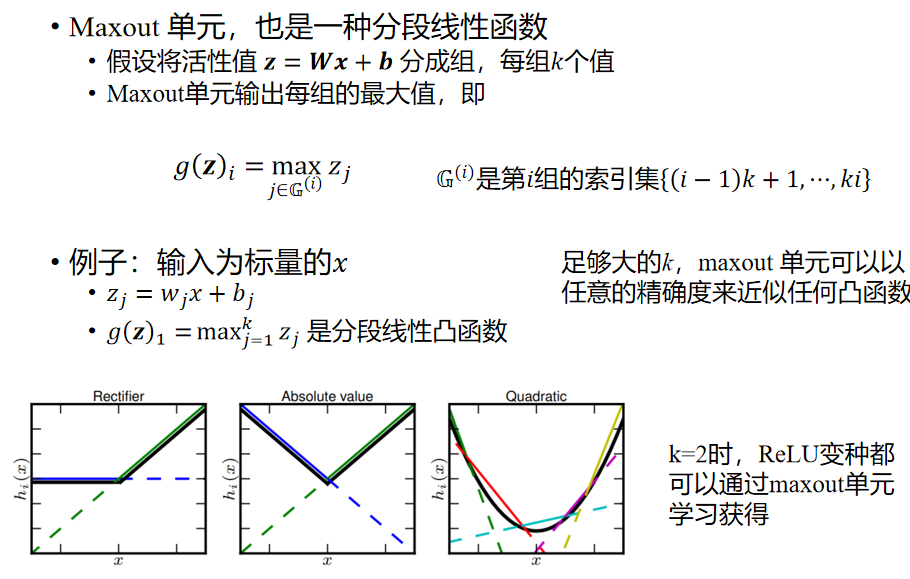
Maxout function

Maxout function comes from a document on ICML <Maxout Networks> , it can be understood as a layer of neural network, similar to pooling layer and convolution layer. We can also regard Maxout function as the activation function layer of the network. The central idea is to fit different functions by using linear functions.

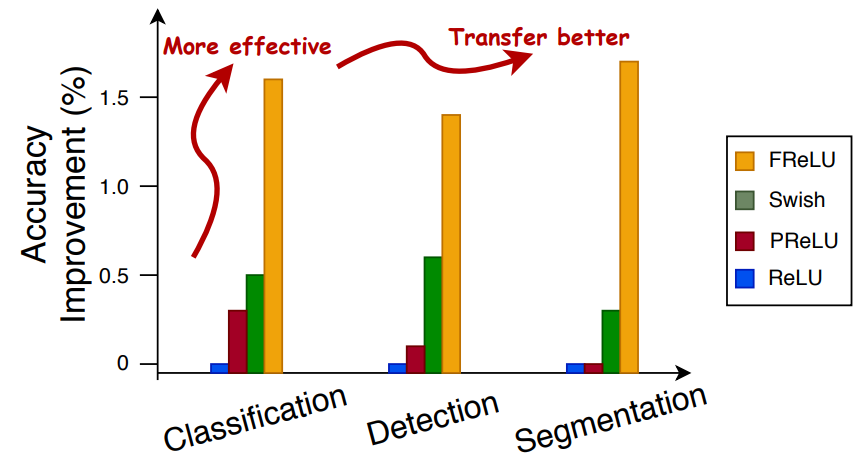
FReLU function

ECCV2020 A new activation function is proposed to realize pixel level spatial information modeling.

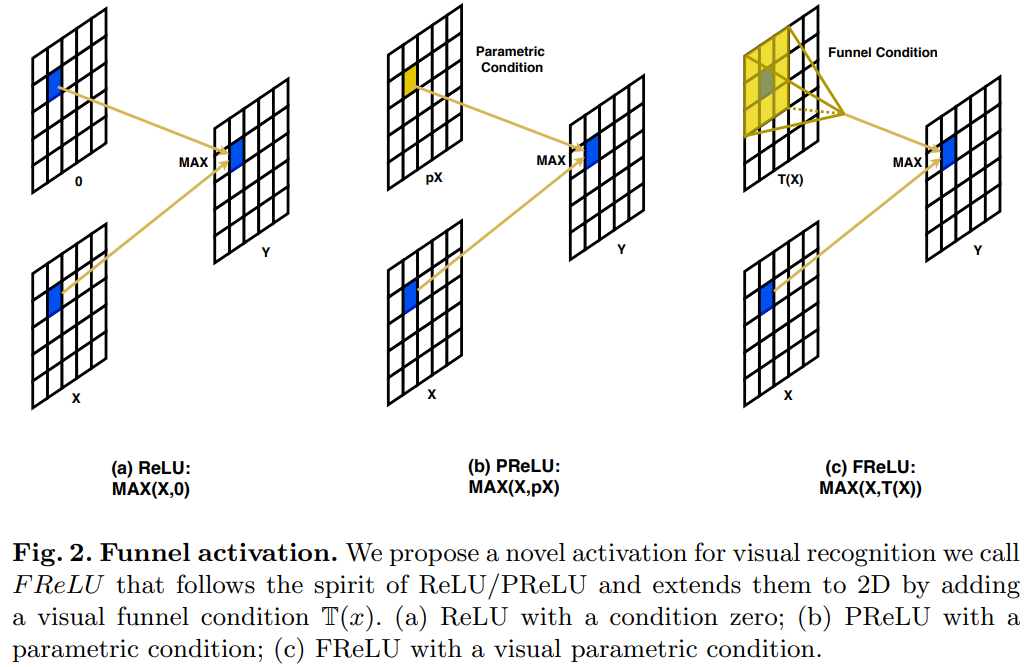
Implementation of T(x) using depth separable convolution DepthWise Separable Conv + BN

class FReLU(nn.Module):
    def __init__(self, c1, k=3):  # ch_in, kernel
        super().__init__()
        self.conv = nn.Conv2d(c1, c1, k, 1, 1, groups=c1, bias=False)
        self.bn = nn.BatchNorm2d(c1)

    def forward(self, x):
        return torch.max(x, self.bn(self.conv(x)))

AconC function

ACON (Activate Or Not) activates the function.
The essence of our commonly used ReLU activation function is a MAX function, and the smooth and differentiable variant of MAX function is called Smooth Maximum.

β Is a smoothing factor. When it approaches infinity, Smooth Maximum becomes the standard MAX function, and when β When it is 0, Smooth Maximum is an arithmetic average operation

Swish activation function is a smooth approximation of ReLU function, which is called ACON-A. The smoothing form can be extended to the ReLU activation function family (PReLU, leaky ReLU), a variant of ACON-B.

Finally, the most extensive form of ACON-C is proposed, that is, it can cover the previous or even more complex forms. In the code implementation, p1 and p2 use two learnable parameters to adapt and adjust.

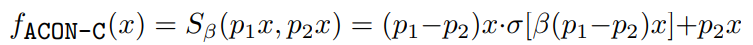
Meta-ACON

As mentioned earlier, the activation function of ACON series passes β To control whether neurons are activated( β Is 0, i.e. inactive). Therefore, we need to design a calculation for ACON β Adaptive function. The design space of adaptive function includes layer wise, channel wise and pixel wise, which correspond to layer, channel and pixel respectively.

class AconC(nn.Module):
    r""" ACON activation (activate or not).
    AconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x, beta is a learnable parameter
    according to "Activate or Not: Learning Customized Activation" <https://arxiv.org/pdf/2009.04759.pdf>.
    """

    def __init__(self, c1):
        super().__init__()
        self.p1 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.p2 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.beta = nn.Parameter(torch.ones(1, c1, 1, 1))

    def forward(self, x):
        dpx = (self.p1 - self.p2) * x
        return dpx * torch.sigmoid(self.beta * dpx) + self.p2 * x


class MetaAconC(nn.Module):
    r""" ACON activation (activate or not).
    MetaAconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x, beta is generated by a small network
    according to "Activate or Not: Learning Customized Activation" <https://arxiv.org/pdf/2009.04759.pdf>.
    """

    def __init__(self, c1, k=1, s=1, r=16):  # ch_in, kernel, stride, r
        super().__init__()
        c2 = max(r, c1 // r)
        self.p1 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.p2 = nn.Parameter(torch.randn(1, c1, 1, 1))
        self.fc1 = nn.Conv2d(c1, c2, k, s, bias=True)
        self.fc2 = nn.Conv2d(c2, c1, k, s, bias=True)
        # self.bn1 = nn.BatchNorm2d(c2)
        # self.bn2 = nn.BatchNorm2d(c1)

    def forward(self, x):
        y = x.mean(dim=2, keepdims=True).mean(dim=3, keepdims=True)
        # batch-size 1 bug/instabilities https://github.com/ultralytics/yolov5/issues/2891
        # beta = torch.sigmoid(self.bn2(self.fc2(self.bn1(self.fc1(y)))))  # bug/unstable
        beta = torch.sigmoid(self.fc2(self.fc1(y)))  # bug patch BN layers removed
        dpx = (self.p1 - self.p2) * x
        return dpx * torch.sigmoid(beta * dpx) + self.p2 * x

This is attached to the paper code