T1 5976. Check whether each row and column contain all integers

For a matrix of size n x n, if each row and column contains all integers from 1 to n (including 1 and N), the matrix is considered to be an effective matrix.

Give you an integer matrix of size n x n, please judge whether the matrix is a valid matrix: If yes, return true; Otherwise, false is returned.

 

 

Problem solving idea: set can be used for de duplication, but the maximum size of n is 100, so we can use array instead of set for de duplication. We just need to traverse each row and column without repeated numbers. If yes, false is returned. No, return true.  

The code and submission results are as follows:

class Solution {
    public boolean checkValid(int[][] matrix) {
        int len = matrix.length;        
        for(int row = 0 ; row < len ; row++){
            int rowN[] = new int[matrix.length+1];
            int colN[] = new int[matrix.length+1];
            for(int col = 0 ; col < len ; col++){
                if(rowN[matrix[row][col]] > 0){
                    return false;
                }else{
                    rowN[matrix[row][col]]++;
                }
                if(colN[matrix[col][row]] > 0){
                    return false;
                }else{
                    colN[matrix[col][row]]++;
                }     
            }            
        }
        return true;   
    }    
}

Summary: because array is used instead of set, the time consumption is reduced from 25ms to 4ms.  

T2 5977. Combine all 1 II with the minimum number of exchanges

Exchange is defined as selecting two different positions in an array and exchanging their values.

A ring array is an array in which the first element and the last element can be considered adjacent.

Give you a binary ring array nums, which returns the minimum number of exchanges required to gather all the 1s in the array at any position.

 

 

 

 

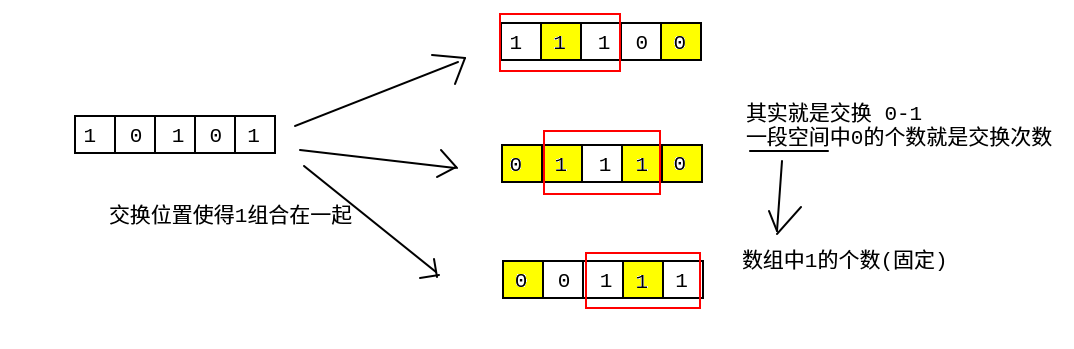
Problem solving idea: sliding window

① Traverse the array to get the number of number 1, which is the size of the window

② Move the sliding window from left to right in the array. The number of numbers 0 in each sliding window is the number of times to be exchanged, because we only need to exchange the number 0 with the number 1 outside the sliding window to meet the problem requirements.

③ The sliding window is moved to the end of the array, and it can be updated continuously for a minimum number of times in the process of moving.

 

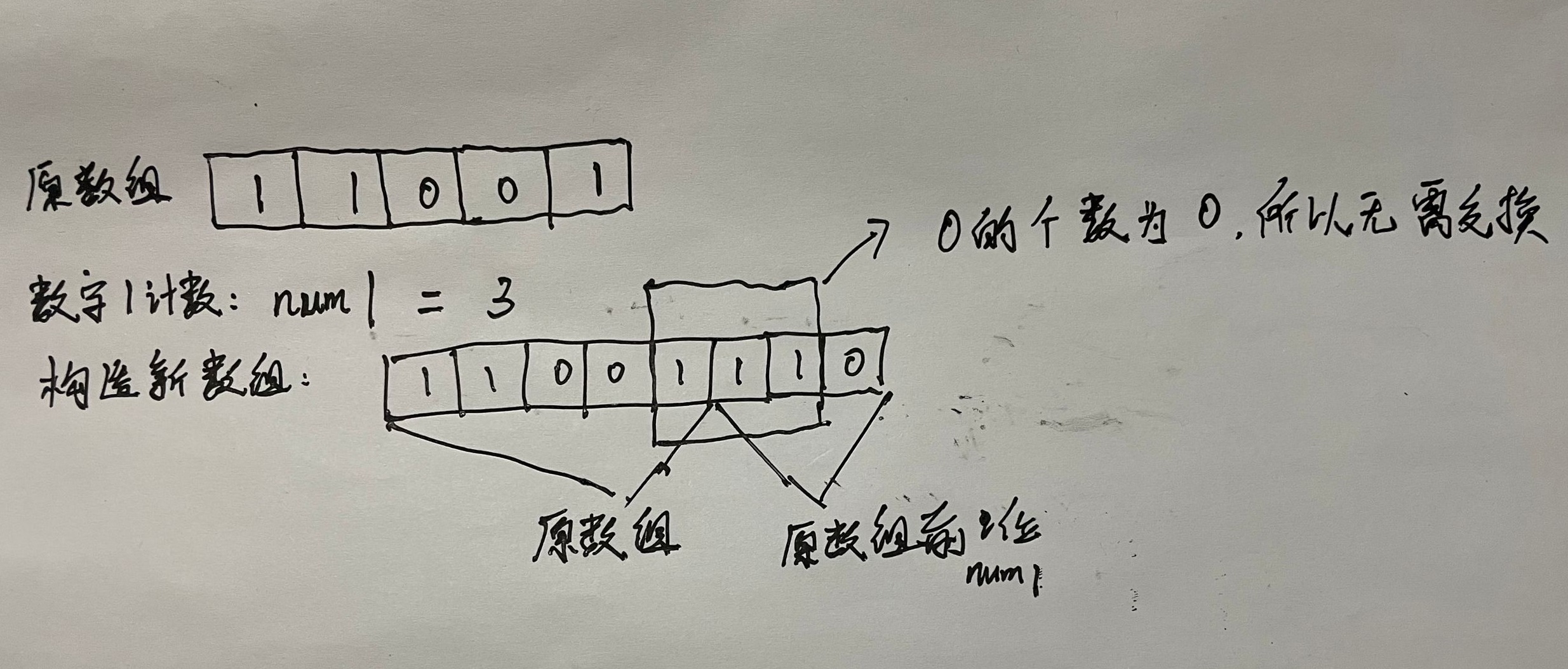
*According to the meaning of the question, the array is circular, so on the basis of the above methods, we can build an array with the length of the original array + the size of the sliding window (the number of digits 1). The new array is composed of the elements of the original array and the size of the sliding window in front of the original array.

Take example 3:

The code and submission results are as follows:

class Solution {
    public int minSwaps(int[] nums) {
        int num1 = 0;
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] == 1) {
                num1++;
            }
        }

        int lNum[] = new int[nums.length + num1];
        for (int i = 0; i < nums.length; i++) {
            lNum[i] = nums[i];
        }
        for(int i = 0 ; i < num1 ; i++){
            lNum[nums.length+i] = nums[i];
        }

        int cnt = 0;
        for(int i = 0; i < num1; i++) {
            if(lNum[i] == 1) {
                cnt++;
            }
        }
        int maxm = cnt;
        for(int i = 1; i <= lNum.length - num1; i++) {
            if(lNum[i-1] == 1) {
                cnt--;
            }
            if(lNum[i+num1-1] == 1) {
                cnt++;
            }
            maxm = Math.max(maxm, cnt);
        }
        return num1 - maxm;   
    }
}

T3 5978. Count the number of words that can be obtained by adding letters 

Give you two string arrays with subscripts starting from 0, startWords and targetWords. Each string consists of only lowercase English letters.

For each string in targetWords, check whether a string can be selected from startWords and perform a conversion operation. The result is equal to the current targetWords string.

The conversion operation is described in the following two steps:

Appends any lowercase letter that does not exist in the current string to the end of the current string.
For example, if the string is "abc", the letters'd ',' e ', or' y 'can be added to the end of the string, but' a 'cannot. If'd 'is appended, the result string is "abcd".
Rearrange the letters in the new string. You can rearrange the letters in any order.
For example, "abcd" can be rearranged to "acbd", "bacd", "cbda", and so on. Note that it can also be rearranged to "abcd" itself.
Find out how many strings in targetWords can be obtained by performing the above conversion operation from any string in startWords. Returns the number of such strings in targetWords.

Note: you can only verify whether the string in targetWords can be obtained by performing an operation on a string in startWords. The string in startWords ， does not actually change during this process.

 

 

Problem solving ideas: 1. State compression (I won't) 2. Sorting + hashset judgment

2. ① sort all elements of the startWords array and store them in hashset.

② traverse the targetWords array, sort each element, and then slide the window to intercept it, using set Contains () determines whether count + + exists, and then break jumps out of the sliding window loop to determine the next element of targetWords. The same method is used. Finally, return count.

The code and submission results are as follows:

class Solution {
    public int wordCount(String[] startWords, String[] targetWords) {
        HashSet<String> set = new HashSet();
        for(int i = 0 ; i < startWords.length ; i++){
            String startTemp = startWords[i];
            char[] cs = startTemp.toCharArray();
            Arrays.sort(cs);
            set.add(new String(cs));
        }
        int count = 0;
        for(int i = 0 ; i < targetWords.length ; i++){
            String targetTemp = targetWords[i];
            char[] ct = targetTemp.toCharArray();
            Arrays.sort(ct);
            String word = new String(ct);
            for(int j = 0 ; j < word.length() ; j++){
                String temp = word.substring(0,j) + word.substring(j+1,word.length());
                if(set.contains(temp)){
                    count++;
                    break;
                }
            }
        }
        return count;
    }
}

Summary: state compression will not. It is said that the time consumption will be significantly reduced after compression.