1, A dance without a boss
Title Description
Ural university has N employees numbered 1~N.
Their relationship is like a tree with the principal as the root, and the parent node is the direct boss of the child node.
Each employee has a happiness index, which is given by the integer Hi, where 1 ≤ i ≤ N.
Now we are going to hold an anniversary party, but no staff is willing to attend the meeting with their direct supervisor.
On the premise of meeting this condition, the organizer hopes to invite some staff to the meeting to maximize the total happiness index of all staff participating in the meeting.
Input format
The first line is an integer N.
Next, line N and line i represent the happiness index Hi of employee i.
Next, in line N-1, enter a pair of integers L and K in each line, indicating that K is the direct supervisor of L.
Output format
Output the largest happiness index.
Sample
sample input
Copy 7 1 1 1 1 1 1 1 1 3 2 3 6 4 7 4 4 5 3 5
sample output
Copy 5
Data range and tips
1≤N≤6000,
−128≤Hi≤127
(1) Topic analysis
Firstly, for the tree dp, the dfs needs to traverse to the leaf node, update the value of the leaf node, and then backtrack and update step by step. Therefore, generally, after scanning to the child nodes, write dfs(v,u) first, and then write the transfer equation. The initial value is assigned as soon as it enters the dfs. There are two types of transfer equations:
① select node class:
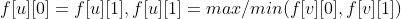
② tree backpacks:
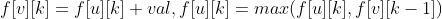
Return to this question. This question obviously uses the first type of selection node. Bosses and subordinates can only leave one side.
(2) Code implementation
#include<cstdio>
#include<algorithm>
using namespace std;
int n,r[6005],head[6005],cnt,root;
int dp[6005][2],ans,in[6005];
struct egde{
int to,next;
}e[6005];
inline void add(int u,int v){//Chained forward star map
cnt++;
e[cnt].next=head[u];
e[cnt].to=v;
head[u]=cnt;
}
inline void dfs(int u,int fa){
dp[u][1]=r[u];//Initial value assignment
dp[u][0]=0;
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
dfs(v,u); //First dfs
dp[u][1]+=dp[v][0];
dp[u][0]+=max(dp[v][1],dp[v][0]);
}
ans=max(dp[u][1],dp[u][0]);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&r[i]);
for(int i=1,u,v;i<n;i++)
scanf("%d%d",&v,&u),add(u,v),in[v]++;
for(int i=1;i<=n;i++){
if(in[i]==0)root=i;
}
dfs(root,-1);
printf("%d",max(dp[root][0],dp[root][1]));
return 0;
} 2, Course selection
Title Description
The school implements the credit system.
Each compulsory course has fixed credits, and must also obtain corresponding elective course credits.
The school offers N elective courses, and the number of optional courses M for each student is given.
Students who take this M course and pass the examination can obtain corresponding credits.
Among the elective courses, some courses can be directly elective, and some courses need some basic knowledge. They can only be elective on the basis of other courses.
For example, Windows programming can only be selected after taking the fundamentals of Windows operation.
We call "Fundamentals of Windows operation" a prerequisite course for "Windows programming".
There is at most one direct prerequisite for each course.
The two courses may have the same prerequisites.
Your task is to determine a course selection scheme for yourself, so that you can get the most credits, and you must meet the prerequisites.
It is assumed that there is no time conflict between courses.
Input format
The first line of the input file includes two integers N and M (separated by a space in the middle), where 1 ≤ N ≤ 300 and 1 ≤ M ≤ N.
The next N lines represent a course, and the course numbers are 1, 2,..., n.
Each line has two numbers (separated by a space). The first number is the class number of the prerequisite course of this course (if there is no prerequisite course, this item is 0), and the second number is the credits of this course.
Credits are positive integers of no more than 10.
Output format
Output an integer representing the total number of credits.
Sample
sample input
Copy 7 4 2 2 0 1 0 4 2 1 7 1 7 6 2 2
sample output
Copy 13
(1) Topic analysis
First of all, this graph is a "forest". When we deal with this problem, we might as well set a total root node '0' or 'n+1' to start. At the same time, the question is "backpack", but not group backpack. We need to use the idea of tree DP, and this problem belongs to the type mentioned above ② tree knapsack class. We set the value of dp[i][j] to represent the maximum credits that can be obtained for the remaining optional j classes with I as the root node. The transfer formula is derived: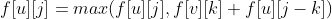
Where u is the root node and v is the child node.
(2) Code implementation
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int N,M,cnt,head[305],in[305],val[305];
int dp[305][305];
struct edge{
int to,next;
}e[305];
inline void add(int u,int v){
cnt++;
e[cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
inline void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==fa)continue;
//printf("v=%d\n",v);
dfs(v,u);
for(int j=M;j>0;j--){// 0 / 1 Backpack
for(int k=j-1;k>=0;k--){
dp[u][j]=max(dp[u][j],dp[u][j-k-1]+dp[v][k]+val[v]);
}
//printf("dp[%d][%d]=%d\n",u,j,dp[u][j]);
}
}
}
int main(){
scanf("%d%d",&N,&M);
for(int i=1,u;i<=N;i++){
scanf("%d%d",&u,&val[i]);
if(u!=0){
add(u,i);
}
else add(N+1,i);//Take 'N+1' as the total root
}
dfs(N+1,-1);
printf("%d",dp[N+1][M]);
} 3, Palace Guard
Title Description
After the incident of the prince of Taiping, Lu Xiaofeng became the first-class bodyguard specially hired by the emperor.
The Imperial Palace starts from the Meridian Gate to the bedroom of the concubines in the harem. It is in the shape of a tree. Some palaces can see each other. The interior is heavily guarded, with three steps and one post and five steps and one sentry. Each palace should be guarded around the clock. The cost of arranging detention centers in different palaces is different.
However, Lu Xiaofeng had insufficient funds and could not place left behind guards in every palace anyway.
Help Lu Xiaofeng arrange bodyguards to minimize the cost on the premise of guarding all the palaces.
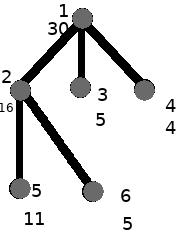
Input format
The input data describes a tree as follows:
The first line n represents the number of nodes in the tree.
From the second line to the n+1 line, each line describes the node information of each palace, in order: the node label i of the palace, the cost k required to place guards in the palace, the number of sons m on this side, and the next M numbers are the labels of M sons of this node.
For a tree with n nodes, the node label is between 1 and N, and the label is not repeated.
Output format
Output the least funds
Sample
sample input
Copy 6 1 30 3 2 3 4 2 16 2 5 6 3 5 0 4 4 0 5 11 0 6 5 0
sample output
Copy 25
Example explanation
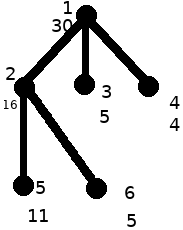
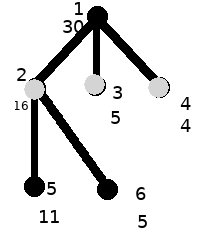
Six areas are arranged as shown in the left figure.
As shown in the figure on the right, guards are arranged in gray dots. Guard 2 can observe 1,2,5,6 and guard 3 can observe 1,3; Guard 4 can observe 1,4.
Total cost: 16 + 5 + 4 = 25
(1) Topic analysis
This topic is different from that of Luogu P2016 strategy game , there is also DP's idea of selecting the best. For any point I, it can be monitored by its own soldiers, its father, and its son. Obviously, it should be the best of the three. Let's set dp[i][3], where the two-dimensional '0' indicates that I will not release the soldier and is monitored by my father‘ 1 'means I won't let the soldier go and is monitored by my son‘ 2 'means I let the soldiers go. But there is another detail: when we decide that I is monitored by my son, one of I's sons must release the soldiers. How can we guarantee it when we choose the best? Let's look at the code.
(2) Code implementation
#include<cstdio>
#include<algorithm>
#define Maxn 1505
#define inf 1e9
using namespace std;
int n,m,cos[Maxn],cnt,head[Maxn],in[Maxn];
int dp[Maxn][3];
//DP [i] [0] -- > I don't let go of the soldiers and is watched by my father
//DP [i] [1] -- > I don't let go of the soldiers and is watched by his son
//DP [i] [2] -- > I release soldiers
struct egde{
int to,next;
}e[Maxn*2];
inline void add(int u,int v){
cnt++;
e[cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
inline void dfs(int u,int fa){
int d=inf;
dp[u][2]=cos[u];
for(int i=head[u];i;i=e[i].next){
int v=e[i].to;
if(v==fa) continue;
//printf("v=%d\n",v);
dfs(v,u);
dp[u][0]+=min(dp[v][2],dp[v][1]);
dp[u][1]+=min(dp[v][2],dp[v][1]);
d=min(d,dp[v][2]-min(dp[v][2],dp[v][1]));//Pay special attention to select the one with the smallest difference between dp[v][2] and dp[v][1], and ensure that at least one son releases the soldier in this case
dp[u][2]+=min(dp[v][2],min(dp[v][1],dp[v][0]));
//printf("dp[%d][1]=%d dp[%d][0]=%d\n",v,dp[v][1],v,dp[v][0]);
}
dp[u][1]+=d;//Make up the difference
//printf("tot=%d cnt=%d\n",tot,cnt);
//printf("u=%d dp[%d][1]=%d dp[%d][0]=%d\n",u,u,dp[u][1],u,dp[u][0]);
}
int main(){
scanf("%d",&n);
//printf("%d\n",n);
for(int i=1,u,k;i<=n;i++){
scanf("%d%d%d",&u,&k,&m);
//printf("%d %d %d ",u,k,m);
cos[u]=k;
for(int j=1,v;j<=m;j++){
scanf("%d",&v);
//printf("%d ",v);
add(u,v);in[v]++;
}
//printf("\n");
}
for(int i=1;i<=n;i++){
if(in[i]==0){
dfs(i,0);
printf("%d",min(dp[i][2],dp[i][1]));
break;
}
}
return 0;
} *** ↗