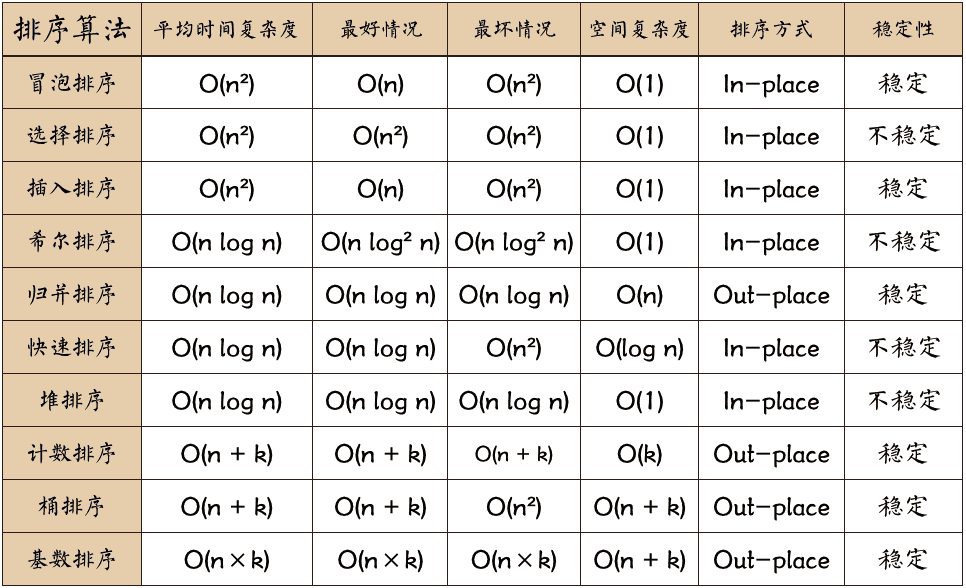
Top ten sorting algorithms
Common sorting algorithms include bubble sort, selection sort, insertion sort, merge sort, quick sort, Hill sort, heap sort, count sort, bucket sort and cardinal sort
Bubble sorting
When adjacent elements are equal, they do not exchange positions, so bubble sorting is a stable sorting.
void bubbleSort(vector<int> & nums){
// Cycle n-1 times
for(int i = 0; i < nums.size() - 1; i++){
// A maximum (small) value is found for each cycle, so the number of cycles per cycle decreases with the increase of i
for(int j = 0; j < nums.size() - i - 1; j++){
//In ascending order, change the large number to the back position
if(nums[j] > nums[j + 1]){
//Exchange two adjacent numbers
swap(nums[j], nums[j + 1]);
}
}
}
}
Select sort
void selectSort(vector<int> & nums){
for(int i = 0; i < nums.size() - 1; i++){ // Cycle n - 1
int minIdx = i; //Loop to find the subscript of the minimum value, and then exchange the minimum value with the starting value
for(int j = i; j < nums.size(); j++){
if(nums[minIdx] > nums[j]){
minIdx = j;
}
}
swap(nums[i], nums[minIdx]);
}
}
Insert sort
void insertSort(vector<int> & nums){
for(int i = 1; i < nums.size(); i++){ // n - 1 cycle
int j;
int num = nums[i];
//Find the first element num[j] less than or equal to the current number forward, and move the subsequent elements backward by one bit
for(j = i - 1; j >= 0; j--){
if(num < nums[j]){ //Move back
nums[j + 1] = nums[j]; //Or swap (Num [J], Num [J + 1]);
}else{
break;
}
}
//Assign num to the next bit of num[j]
nums[j + 1] = num;
}
}
Shell Sort
Hill sort, also known as decreasing incremental sort algorithm, is a more efficient improved version of insertion sort. But Hill sorting is an unstable sorting algorithm.
Hill sort is an improved method based on the following two properties of insertion sort:
- Insertion sorting is efficient when operating on almost ordered data, that is, it can achieve the efficiency of linear sorting;
- However, insertion sorting is generally inefficient, because insertion sorting can only move data one bit at a time;
The basic idea of Hill sort is: first divide the whole record sequence to be sorted into several subsequences for direct insertion sort. When the records in the whole sequence are "basically orderly", then directly insert sort all records in turn.
void shell_sort(vector<int> & nums) {
//Increment gap and gradually reduce the increment
for (int gap = nums.size() / 2; gap > 0; gap /= 2) {
//From the gap element, directly insert and sort the groups one by one
for (int i = gap; i < nums.size(); i++) {
for(int j = i; j >= gap && nums[j] < nums[j - gap]; j -= gap){
swap(nums[j], nums[j - gap]);
}
}
}
}
Merge sort
void merge(vector<int> & vec, int L1, int R1, int L2, int R2){
vector<int> temp; //Auxiliary array
int begin = L1;
while(L1 <= R1 && L2 <= R2){
if(vec[L1] < vec[L2]){
temp.push_back(vec[L1++]);
}else{
temp.push_back(vec[L2++]);
}
}
while(L1 <= R1){
temp.push_back(vec[L1++]);
}
while(L2 <= R2){
temp.push_back(vec[L2++]);
}
vec.assign(temp.begin(), temp.end());
}
void mergeSort(vector<int> & vec, int left, int right){
if(left < right){
int mid = (left + right) / 2;
mergeSort(vec, left, mid);
mergeSort(vec, mid + 1, right);
merge(vec, left, mid, mid + 1, right);
}
}
Quick sort
Why is quick sort called quick sort?
https://blog.csdn.net/weixin_41445507/article/details/90255906
https://blog.csdn.net/linfeng24/article/details/38429055
int quick(vector<int> & vec, int left, int right){
int temp = vec[left];
while(left < right){
//Find the first number on the left that is greater than or equal to temp
while(left < right && vec[left] < temp){
left += 1;
}
//Find the first number on the right that is less than or equal to temp
while(left < right && vec[right] > temp){
right -= 1;
}
//Exchange two numbers
swap(vec[left], vec[right]);
}
return left;
}
void quickSort(vector<int> & vec, int left, int right){
if(left < right){
int pos = quick(vec, left, right);
quickSort(vec, left, pos - 1);
quickSort(vec, pos + 1, right);
}
}
Heap sort
Heap sort refers to a sort algorithm designed by using the data structure of heap. Heap is a structure similar to a complete binary tree, and satisfies the nature of heap at the same time: that is, the key value or index of a child node is always less than (or greater than) its parent node. Heap sort can be said to be a selective sort that uses the concept of heap to sort. There are two methods:
- Large top heap: the value of each node is greater than or equal to the value of its child nodes, which is used for ascending arrangement in heap sorting algorithm;
- Small top heap: the value of each node is less than or equal to the value of its child nodes, which is used for descending arrangement in heap sorting algorithm;
The average time complexity of heap sorting is Ο (nlogn).
// Build large top reactor
void buildMaxHeap(vector<int> & nums) {
// Adjust the heap of each non leaf node
for (int i = nums.size() / 2; i >= 0; i--) {
heapify(nums, i);
}
}
// Heap adjustment, starting from the ith node
void heapify(vector<int> & nums, int i, int size) {
int left = 2 * i + 1; //Left child
int right = 2 * i + 2; //Right child
int largest = i;
//Find the maximum of the left and right children
if (left < size && nums[left] > nums[largest]) {
largest = left;
}
if (right < size && nums[right] > nums[largest]) {
largest = right;
}
//Replace with parent node
if (largest != i) {
swap(nums[i], nums[largest]);
heapify(nums, largest);
}
}
void heapSort(vector<int> & nums) {
buildMaxHeap(nums);
for (int i = nums.size() - 1; i > 0; i--) {
// Put the top node last each time
swap(nums[0], nums[i]);
heapify(nums, 0, i);
}
return nums;
}
Count sort
Counting sorting is not a comparative sorting, and the sorting speed is faster than any comparative sorting algorithm.
Since the length of the array used for counting depends on the range of data in the array to be sorted (equal to the difference between the maximum and minimum values of the array to be sorted plus 1), counting sorting requires a lot of time and memory for arrays with large data range.
void countingSort(vector<int> & nums) {
int maxValue = nums[0];
//Find maximum value
for(int i = 1; i < nums.size(); i++){
maxValue = max(maxValue, nums[i]);
}
vector<int> bucket(maxValue + 1, 0);
for (int i = 0; i < maxValue + 1; i++) {
bucket[nums[i]] += 1;
}
int idx = 0;
for (int i = 0; i < maxValue + 1; i++) {
while(bucket[i] > 0) {
nums[idx++] = i;
bucket[i] -= 1;
}
}
}
Bucket sorting
Bucket sorting is an upgraded version of counting sorting. It makes use of the mapping relationship of the function. The key to efficiency lies in the determination of the mapping function. In order to make bucket sorting more efficient, we need to do these two things:
- When there is enough extra space, try to increase the number of barrels
- The mapping function used can evenly distribute the input N data into K buckets
At the same time, for the sorting of elements in the bucket, it is very important to choose a comparative sorting algorithm for the performance.
- When is the fastest
When the input data can be evenly distributed to each bucket.
- When is the slowest
When the input data is allocated to the same bucket.
Cardinality sort
Radix sorting is a non comparative integer sorting algorithm
Cardinal sorting, counting sorting and bucket sorting all use the concept of bucket, but there are obvious differences in the use of bucket:
- Cardinality sorting: allocate buckets according to each number of key value;
- Counting and sorting: only one key value is stored in each bucket;
- Bucket sorting: each bucket stores a certain range of values;