after studying the shortest path problem for one day, I found that there are many solutions to the shortest path problem. BFS,DFS, A *, and many other algorithms can solve the shortest path problem, so I plan to solve DFS first and summarize the shortest path problem next time.
like BFS, DFS is a search algorithm. BFS is implemented in the form of diffusion + queue, while DFS is different. After all, it is depth first. DFS will use recursion to deeply explore a path. When a path is explored to the end, it will return to the upper level node and then explore. This reminds us of the nature of stack. Therefore, BFS is diffusion + queue, and DFS is recursion + stack.
When using BFS, we will find that the code implementation is more complex, and DFS uses the idea of recursion, so naturally DFS also adheres to the advantage of concise recursive code.
Give an example with a question.
It's still the problem of red and black bricks made in BFS
BFS idea:
Every time from the starting point, look around for appropriate points, press them into the queue as new nodes, and pop the upper level nodes out of the queue.
DFS idea:
From the starting point, walk around every time according to "top left and bottom right" (it can be seen that "down" should actually be the way to return to the upper level node)
DFS Code:
#include<bits/stdc++.h>
using namespace std;
int dir[4][2]={{-1,0},{0,1},{1,0},{0,-1}},num,Wx,Hy;
char room[23][23];
bool CHECK(int x,int y)
{
if(x<Wx&&x>=0&&y>=0&&y<Hy)
return true;
else
return false;
}
struct node
{
int x,y;
}node1;
void DFS(int x,int y)
{
room[x][y]='#';
num++;
for(int i=0;i<4;i++)
{
node1.x=x+dir[i][0];
node1.y=y+dir[i][1];
if(CHECK(node1.x,node1.y)&&room[node1.x][node1.y]=='.')
{
DFS(node1.x,node1.y);/*Recursive embodiment*/
}
}
}
int main()
{
int t,dx,dy;
for(cin>>t;t;t--)
{
cin>>Wx>>Hy;
num=0;
for(int i=0;i<Wx;i++)
{
for(int j=0;j<Hy;j++)
{
cin>>room[i][j];
if(room[i][j]=='@')
{
dx=i;
dy=j;
}
}
}
DFS(dx,dy);
cout<<num<<endl;
}
return 0;
}
Previous BFS code
#include <iostream>
#include <queue>
using namespace std;
char room[23][23];
int WX,HY;
int dir[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
#define CHECK(x,y) (x>=0&&x<=WX&&y>=0&&y<=HY)
struct node
{
int x,y;
};
int num;
void BFS(int dx,int dy)
{
num=1;
queue <node> q;
node start,next;
start.x=dx;
start.y=dy;
q.push(start);
while(!q.empty())
{
start=q.front();
q.pop();
cout<<start.x<<" "<<start.y<<endl;
for(int i=0;i<4;i++)
{
next.x=start.x+dir[i][0];
next.y=start.y+dir[i][1];
if(CHECK(start.x,start.y)&&room[next.x][next.y]=='.')
{
num++;
q.push(next);
room[next.x][next.y]='#';
}
}
}
}
int main()
{
int t,dx,dy;
for(cin>>t;t;t--)
{
cin>>WX>>HY;
if(WX==0&&HY==0)
{
cout<<0<<endl;
continue;
}
for(int i=0;i<WX;i++)
{
for(int j=0;j<HY;j++)
{
cin>>room[i][j];
if(room[i][j]=='@')
{
dx=i;
dy=j;
}
}
}
num=0;
BFS(dx,dy);
cout<<num<<endl;
}
}
Core code comparison
void DFS(int x,int y)
{
room[x][y]='#';
num++;
for(int i=0;i<4;i++)
{
node1.x=x+dir[i][0];
node1.y=y+dir[i][1];
if(CHECK(node1.x,node1.y)&&room[node1.x][node1.y]=='.')
{
DFS(node1.x,node1.y);/*Recursive embodiment*/
}
}
}
void BFS(int dx,int dy)
{
num=1;
queue <node> q;
node start,next;
start.x=dx;
start.y=dy;
q.push(start);
while(!q.empty())
{
start=q.front();
q.pop();
cout<<start.x<<" "<<start.y<<endl;
for(int i=0;i<4;i++)
{
next.x=start.x+dir[i][0];
next.y=start.y+dir[i][1];
if(CHECK(start.x,start.y)&&room[next.x][next.y]=='.')
{
num++;
q.push(next);
room[next.x][next.y]='#';
}
}
}
}
It is not difficult to see that DFS is much better than BFS after adopting the idea of recursion.
The graphics are explained below
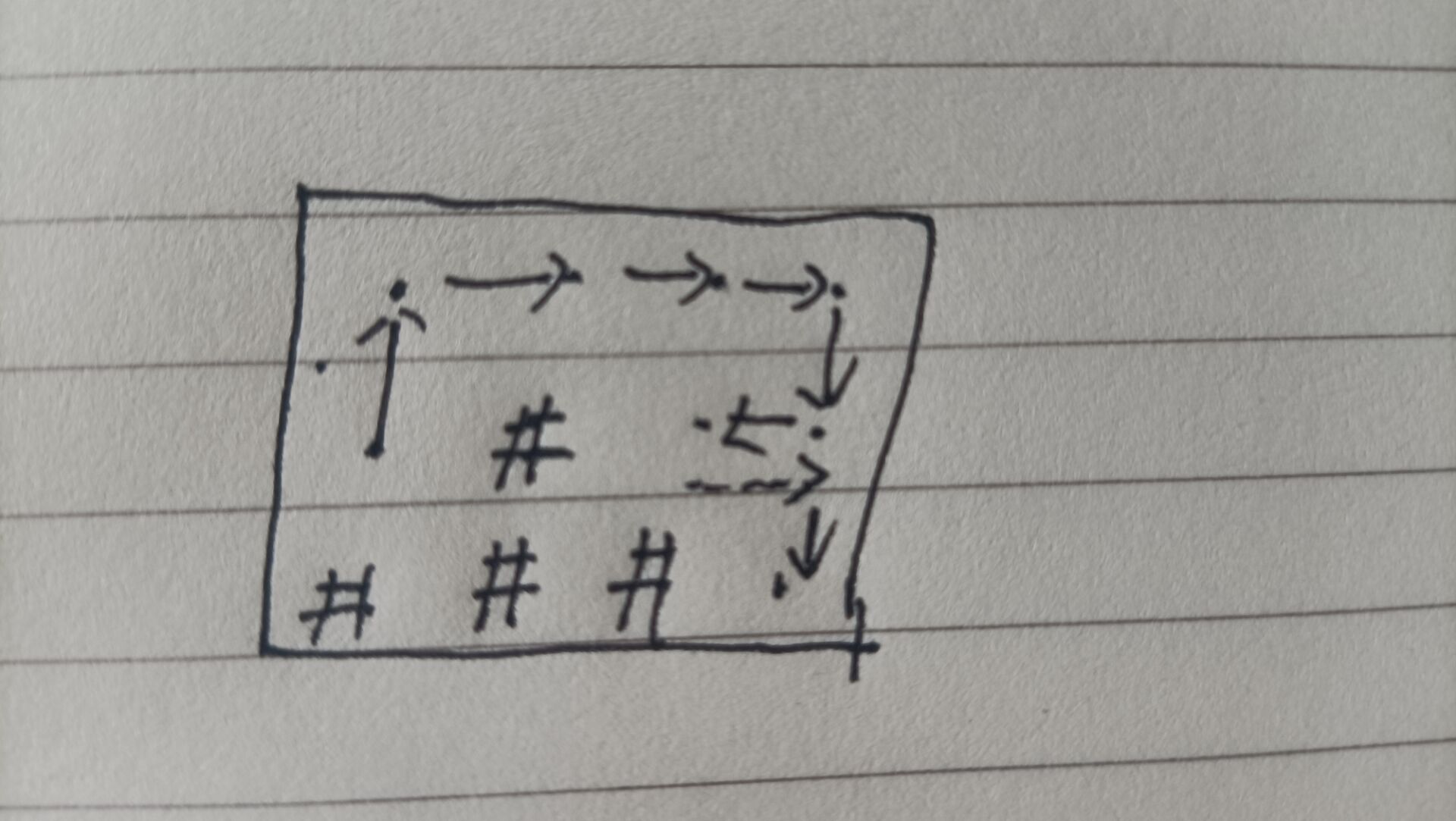
The dotted line represents return and the realization represents forward. When we look at the code, we don't actually return this operation.
But here
for(int i=0;i<4;i++)
{
node1.x=x+dir[i][0];
node1.y=y+dir[i][1];
if(CHECK(node1.x,node1.y)&&room[node1.x][node1.y]=='.')
{
DFS(node1.x,node1.y);/*Recursive embodiment*/
}
}
if the if statement is judged as yes, it will continue to execute the deep call of internal DFS. If the if statement is judged as no, it will automatically return to the previous layer of DFS circular statements to change the direction. This process of "returning to the previous layer" is actually returning. Basically, it can be said that the if statement plays a role in controlling forward and backward.
Finally, we will get a num value that traverses all places.
Although DFS is easy to write with recursive skills, we may inevitably encounter such a tree when we do some problems,
this way is very, very deep, so we will waste a lot of resources when exploring with recursion. If there is no correct answer in this way, it will be the worst result. Therefore, there is the idea of combining DFS and BFS. Simply say it here and write it tomorrow.
this idea is to specify a depth. Assuming that it is 5, we first conduct a deep search in the range of 5. If we can't find it, we will deepen it by 5 and continue to search repeatedly. In this way, we can avoid going all the way to the dark.