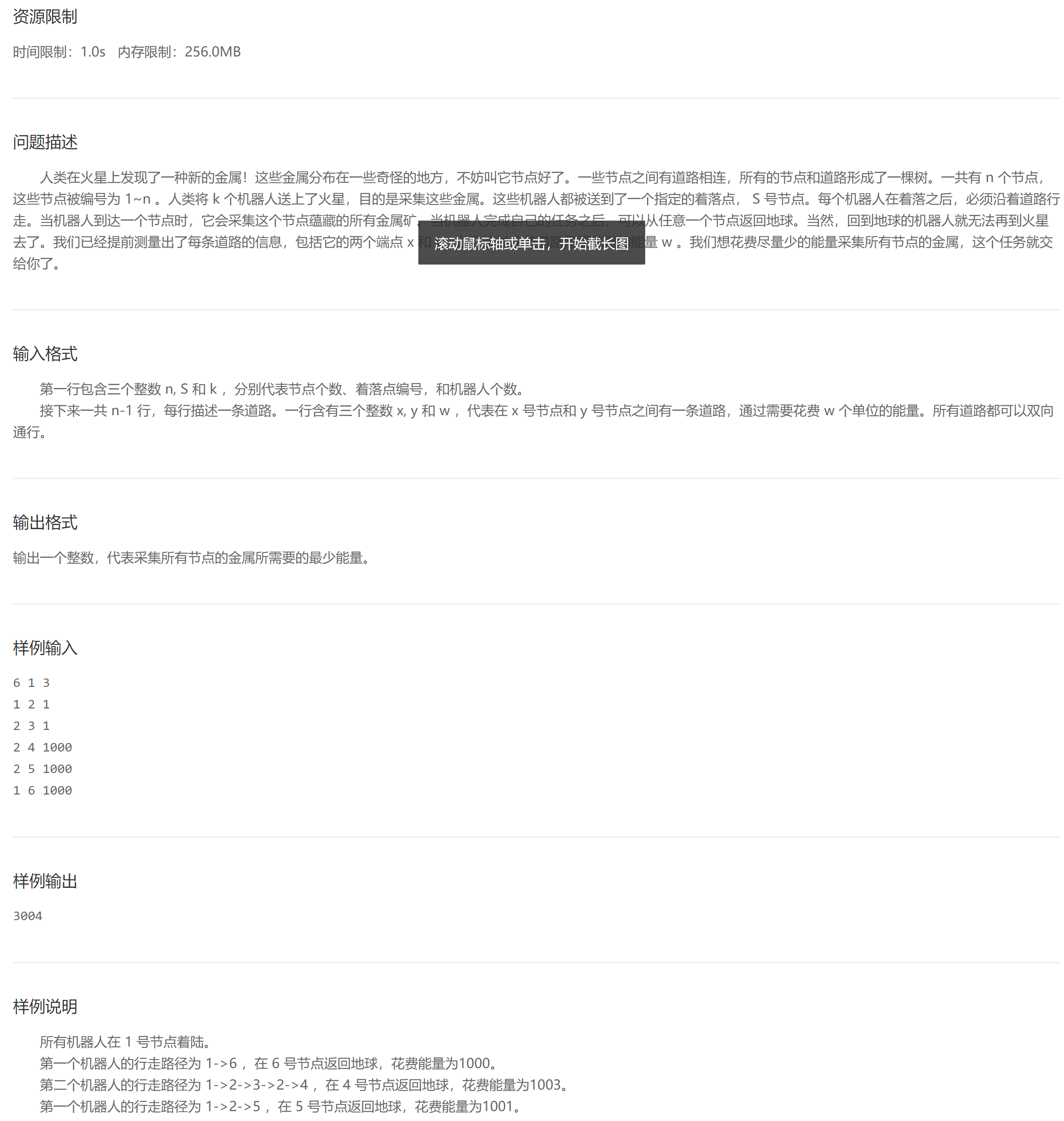
A. metal collection
Searched. It's found that it's a tree dp. This thing really doesn't, and it hasn't been done... So I can't understand it for the time being..
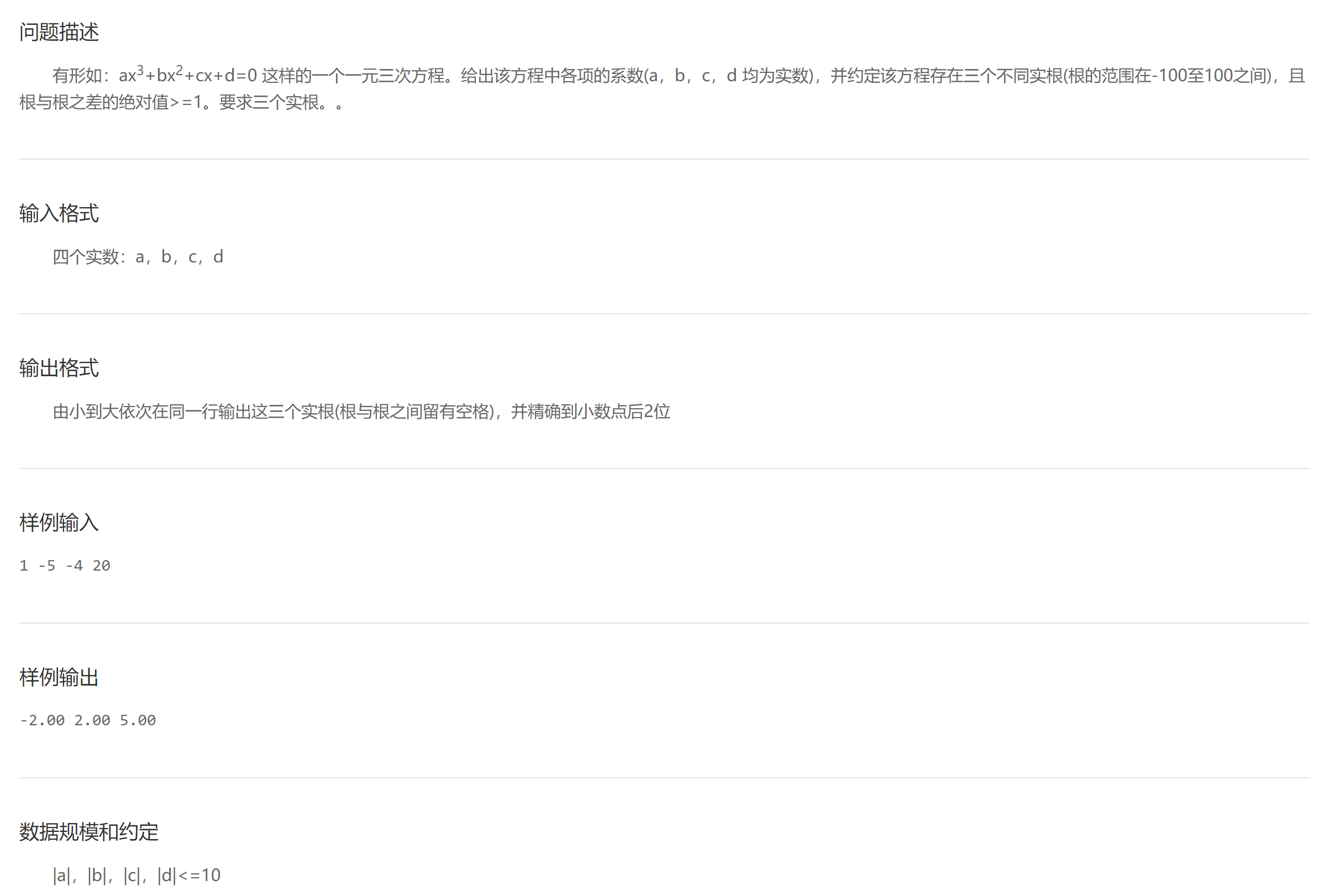
B solution of univariate cubic equation
- Solution idea: use floating-point numbers to enumerate from negative numbers to positive numbers. According to the position of the root in mathematics, the multiplication of the function values of the left and right positions must be less than 0 (different sign).
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d,i;
int main()
{
cin >>a>>b>>c>>d;
//First, use enumeration to preliminarily determine the range of the three roots,
//For example, if f [i] * f [i + 1] < 0, you can know that there is a root between [i,i+1]
for(i=-100;i<=100;i+=0.01){
double x1=i-0.005,x2=i+0.005;
if((x1*x1*x1+b/a*x1*x1+c/a*x1+d/a)*(x2*x2*x2+b/a*x2*x2+c/a*x2+d/a)<0)
printf("%.2f ",i);
}
return 0;
}
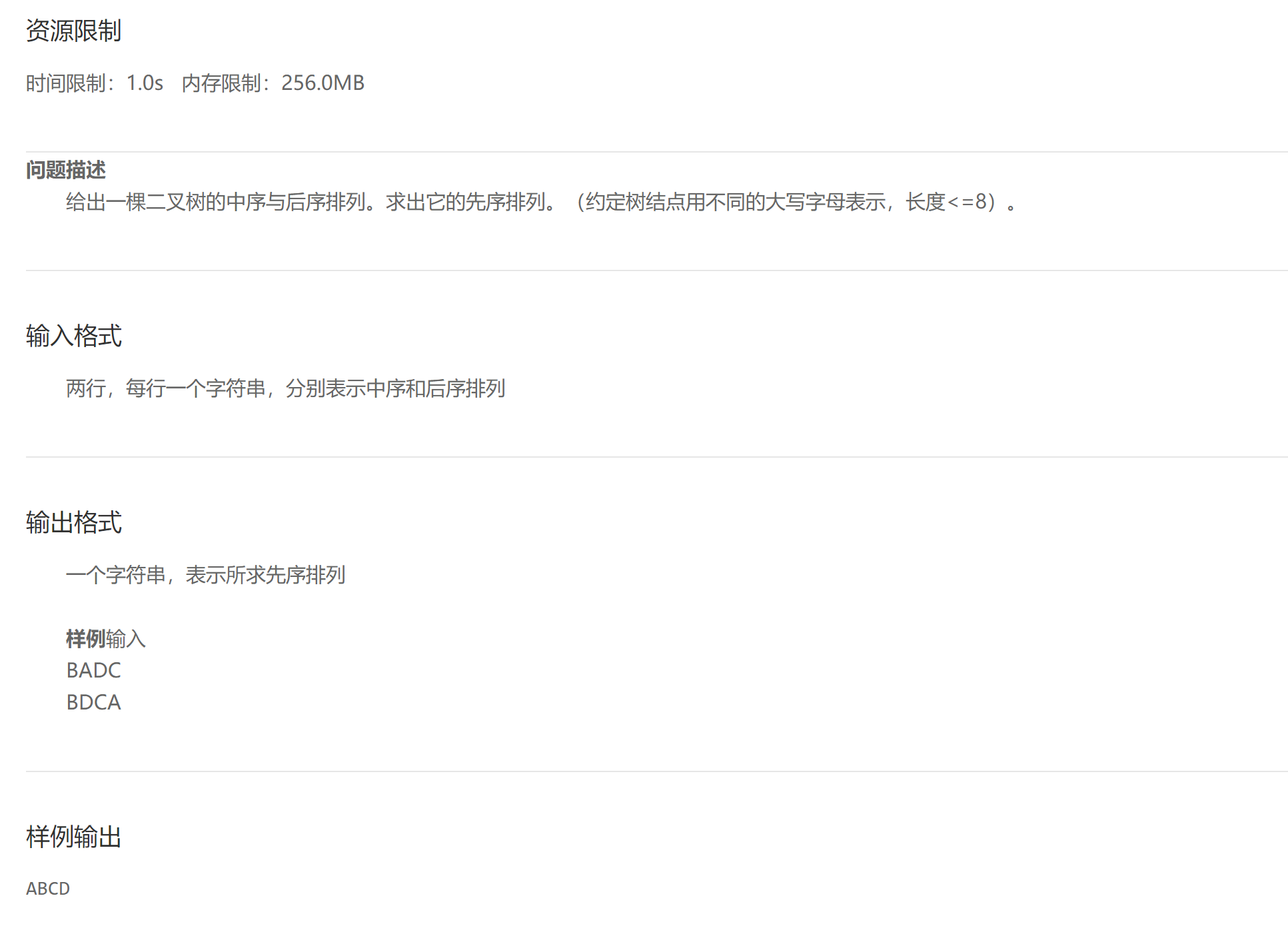
C ordering
- Problem solving ideas: this kind of questions are very common in the interview. If you give middle order + first order or second order, you should determine a binary tree sequence. Similarly, whether you give middle order + first order or middle order + second order, we can build the binary tree through various ergodic characteristics and recursive divide and conquer.
- Priority arrangement: root node + left subtree + right subtree
- Middle order arrangement: left subtree + root node + right subtree
- Post order arrangement: left subtree + right subtree + root node
Finally, we can instantly determine the position of the root node according to the first order \ second order, and according to the position of the root node in the middle order, we can determine the position of the left subtree and the right subtree, and then recursive divide and conquer can realize a way to build a binary tree. This problem needs to build a first order arrangement, so we need to print the root node at the position where the left and right subtrees are not formed.
- Small details: find the location of the root node in the middle order, which can be recorded in advance through the hash table (this kind of middle order is generally a tool man).
#include <bits/stdc++.h>
using namespace std;
string post,in;
int memo[26];
void pre(int root, int start, int end) {
if(start > end) return ;
int i = memo[post[root]-'A'];
printf("%c", post[root]);
//Left subtree
pre(root - 1 - end + i, start, i - 1);
//Right subtree
pre(root - 1, i + 1, end);
}
int main() {
cin>>in>>post;
memset(memo,0,sizeof(memo));
for(int i=0;i<in.size();i++){
memo[in[i]-'A'] = i;
}
pre(post.size()-1,0,post.size()-1);
return 0;
}
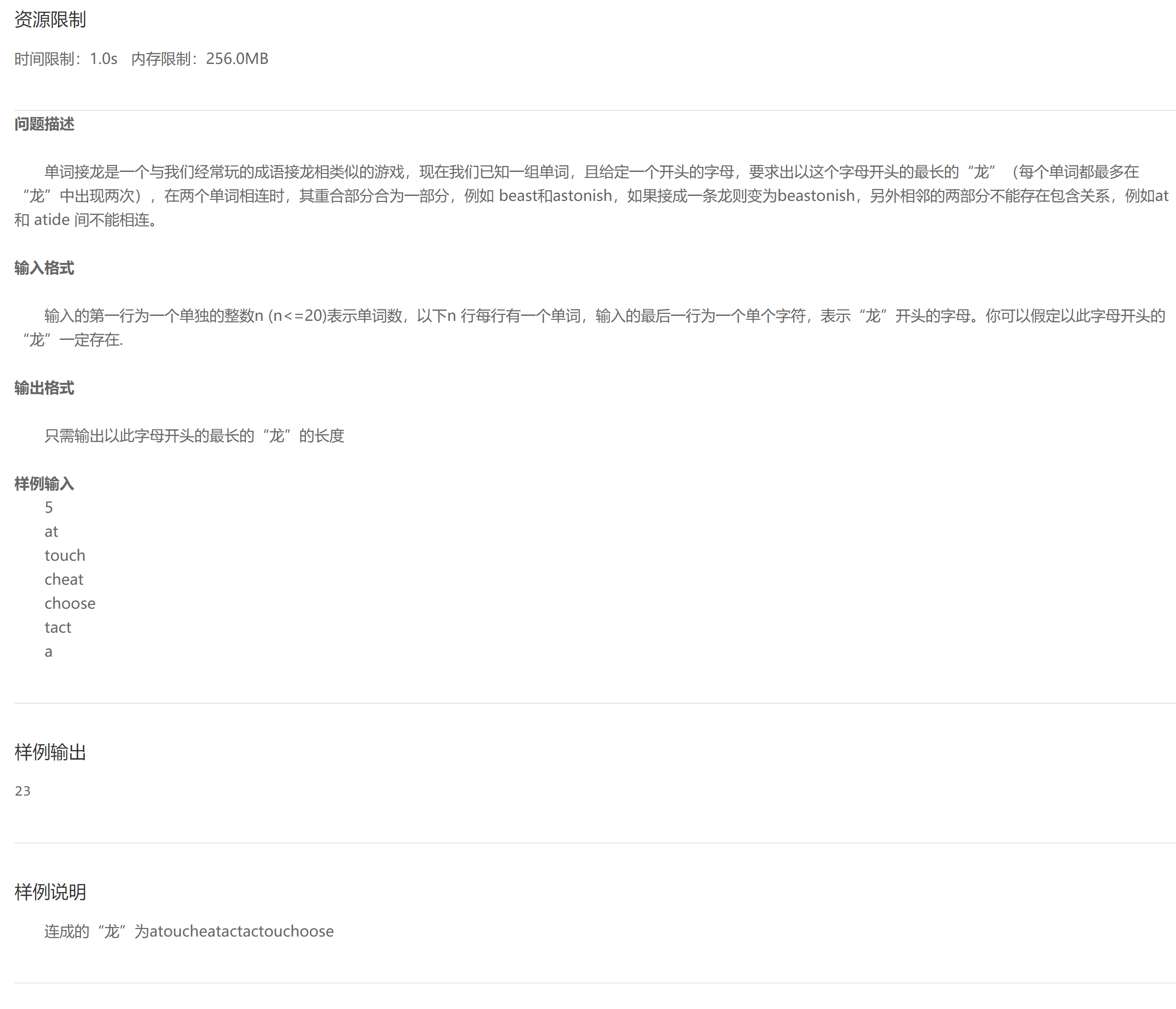
D word Solitaire
- Problem solving ideas: three steps
- Use adjacency matrix preprocessing to record the common minimum contiguous tail of any two numbered words (when the minimum contiguous tail is the previous word itself, it is not allowed).
- Create a table that records the number used.
- For the dfs burst search results, note that the use times and answers need to be updated for each selection. Whether it can be selected depends on whether there is a minimum border at the tail and the selected times cannot exceed twice!
On the updating method of adjacency matrix: it is very common to enumerate and traverse the minimum result with the substr() method of string, and then record it through a two-dimensional array. I use the idea of finite state automata to update the answer... Anyone who has learned a little about automata should be able to understand it.. These are the two update methods I can think of. You can also try other methods.
I also recently wrote some topics on automata, so I think about automata...
#include<bits/stdc++.h>
using namespace std;
int n;char start;
vector<string>s(25);
int mp[25][25];
int used[25]; // Number of times each word is used
int ans = 0;
//Enumerate and add the update length of the next selected word according to whether there are coincident characters at the end of the word chain
void dfs(int pos,int len)
{
ans = max(len, ans);
//Record usage times
used[pos] ++ ;
for (int i = 0; i < n; i ++ )
//If there can be a common tail and the number of uses is less than 2, the length will become len + s [i] size()-mp[pos][i]
if (mp[pos][i] && used[i] < 2)
dfs(i, len+(int)s[i].size()-mp[pos][i]);
used[pos] -- ; // Undo usage times
}
//Function for arbitrarily updating the adjacency matrix of two words (storing the minimum common length at the end of two words)
void get_same(const string&s1,const string&s2,int x1,int x2){
int state = 1;
int len1 = s1.size(),len2 = s2.size();
int i = 0,j=0;
int cnt = 0;
int res = INT_MAX;
while(i<len1&&j<len2){
//State 1 is the case that two characters are not equal. Once they are equal, it enters state 2
if(state==1){
cnt = 0;
j = 0;
if(s1[i]==s2[j])
state = 2;
else i++;
}//In state 2, the two characters are now equal. If it can pop up at last, continue to judge
else if(state==2){
if(s1[i]==s2[j]){
i++;
j++;
cnt++;
if(i==len1){
res = min(res,cnt);
j = 0;
i = i-cnt+1;
state = 1;
}
}else{
state = 1;
}
}
}
if(res!=len1&&res!=INT_MAX)
mp[x1][x2] = res;
}
//Construct adjacency matrix to record whether any two words can be connected and the maximum repetition
void pre_handle(){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
get_same(s[i],s[j],i,j);
}
}
}
int main(){
memset(mp, 0,sizeof(mp));
memset(used,0,sizeof(used));
cin>>n;
for(int i=0; i<n; i++)
cin>>s[i];
cin>>start;
pre_handle();
//Search for the first word
for(int i=0;i<n;i++){
if(s[i][0]==start){
dfs(i,(int)s[i].size());
}
}
cout<<ans;
}
E trees outside the school gate

- Problem solving ideas:
At first glance, this is the problem of interval division intersection, and the amount of data is small. You can directly map interval elements with an array (see the code for details, which should be easy to understand)
Summary articles on various interval scheduling problems seen a few days ago: Interval scheduling problem
#include<bits/stdc++.h>
using namespace std;
int check[10001];
int L,M;
int main(){
memset(check,0,sizeof(check));
cin>>L>>M;
for(int i=0;i<M;i++){
int a,b;
cin>>a>>b;
for(int j=a;j<=b;j++){
check[j]++;
}
}
//Record how many trees to cut
int count = 0;
for(int i=0;i<=L;i++)
if(check[i])
count++;
cout<<L+1-count;
}
F. competition arrangement

- Problem analysis: note that input an N, and then determine that there are 2 N-th teams, and you need to arrange the game with 2 n-th-1 day.
The problem of arranging two teams to play is obvious C n 2 C^{2}_{n} Cn2 , the problem of finding combination. - Focus on two points:
- Output in days, and each team can only compete once a day (so the daily combination needs to judge whether it has competed before combination)
- Teams that have competed in the past cannot compete again (so the combination output every day cannot be the same, that is, a hash table recording a pair of data is required (of course, the amount of data here is small, which can be replaced by a large array without hash conflict))
#include <bits/stdc++.h>
using namespace std;
int main() {
//check1 is used to mark that the team has competed on that day, and check2 is used to mark that the two teams have competed
//Because the amount of data is small, arrays can be used to replace hash tables
int n, m;
//check1 is a hash table for one day, so it needs to be reset on another day
//check2 is a hash table for the whole day process, so it does not need to be reset
bool check1[1000], check2[10000] = {0};
cin >> n;
m = pow(2, n);
//The outer layer cycle record is currently the day. The inner layer is equivalent to taking two out of m for output, but it should be ensured that the teams that have competed in the previous days cannot be output, and one team cannot compete twice on that day
for (int i = 1; i <= m - 1; i++) {
memset(check1, 0, sizeof(check1));
printf("<%d>", i);
for (int j = 1; j <= m; j++) {
if (check1[j] == 0) {
for (int k = j + 1; k <= m; k++) {
if (check2[j * 100 + k] == 0 && check1[k] == 0) {
printf("%d-%d ", j, k);
check2[j * 100 + k] = 1;
check1[j] = check1[k] = 1;
break;
}
}
}
}
cout << endl;
}
return 0;
}