V1 Strict Disclaimer
This part of the content is abstracted from Baidu Encyclopedia and exempted from liability after declaration.
V2 Pull and spit
Want to experience what despair is?
Try this question and make sure you suspect life.QwQ
(Big man, please skip)
Here is the topic
(Super Details)
1 Conceptual View Details click
1.1 Balanced Binary Tree
Balanced Binary Tree has the following properties:
It is an empty tree or its left and right subtrees have absolute height differences of no more than 1, and both subtrees are balanced binary trees.
The common implementation methods of balanced binary tree are red-black tree, AVL, scapegoat tree, Treap, stretch tree, etc.
Because only Treap is used in arctium, and Treap is not familiar with it, Treap is used.
1.2 Treap
Treap is a binary sorted tree. Its left subtree and right subtree are Treap, respectively.
Unlike a general binary sort tree, Treap records an extra piece of data, the priority.
Treap satisfies the nature of the heap while forming a binary sorting tree with key codes
(Here we assume that the priority of a node is greater than that of its children).
Moreover, Treap has a "BST" property:
-
The key code of this node is not less than that of any node in its left subtree.
-
The key code of this node is not greater than that of any node in its right subtree.
2 Process
2.1 Definition
This Treap requires support for the following operations:
-
Insert x Number
-
Delete the x number (if there are multiple identical numbers, only one should be deleted)
-
Query the rank of x numbers (rank is defined as the number of decimal digits less than the current number +1+1).If there are multiple identical numbers, the lowest rank should be output)
-
Number of queries ranked x
-
Precursor to x (precursor defined as less than x and maximum number)
-
Ask for the succession of x (succession defined as a number greater than x and minimum)
So we need to define the following structure variables (the reason I'll explain later)
1 struct Treap 2 { 3 int l,r,val,data,num,size; 4 }t[100005];
l: Left Child
r: Right child
val: The key code of the node
data: Priority of the node
num: How many nodes (counting themselves) are equal to the current node's val ue, i.e. $"number of copies"$
size: how many descendants of a node (to count in itself)
Get a new point
- Depth++;
- Assignment;
- Randomly assign priority;
- Number of copies is 1 (counts itself)
- Size is 1 (counts in itself)
1 int Get_New(int val) 2 { 3 ++law; 4 t[law].val=val; 5 t[law].data=rand(); 6 t[law].num=1; 7 t[law].size=1; 8 return law; 9 }
Find Size
Size = Size of the left child + Size of the right child + number of copies of itself.
1 void Update(int &p) 2 { 3 t[p].size=t[t[p].l].size+t[t[p].r].size+t[p].num; 4 }
Build Trees
-
Insert a point of negative infinity size (root node)
-
Insert a point of positive infinite size (the right node of the root node)
The purpose is to prevent the balance tree from degenerating into chains
1 void Building() 2 { 3 Get_New(INT_MIN); 4 Get_New(INT_MAX); 5 root=1,t[1].r=2; 6 Update(root); 7 }
2.2 Insert Elements
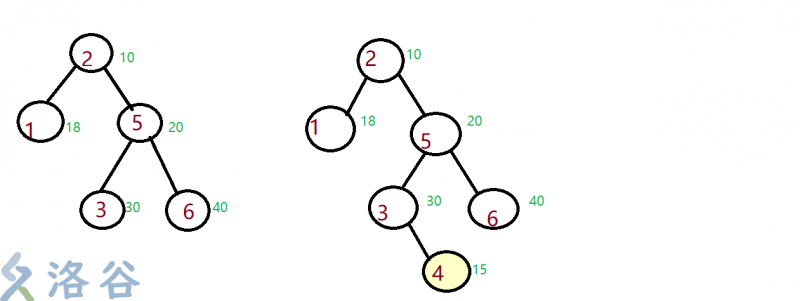
2.2.1 Introduction
As shown in the figure above, there is a balanced binary tree with black numbers inside the circle representing the key codes of the nodes.
The number of red around the circle represents the priority of the nodes (assuming that the nature of the root heap has not been maintained).
In this case, insert the number 4 into the balanced binary tree.
2.2.2 Inserted Rules
Why did 4 become the right son of 3?
In this case, the "BST" property of binary lookup tree is used.(1.21.2 explained, not redundant)
In the data, 4 is greater than 2, so 4 cannot be the son of 1.Again 4 < 5, 4 therefore cannot be the son of 6.
Of all leaf nodes, only 3 satisfied.And because 4 > 3, 4 became the right son of 3.
Furthermore, each inserted node has and only has a suitable location.
2.3 Left and Right Rotation
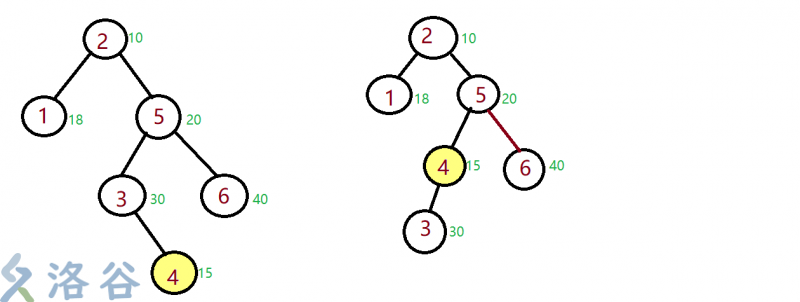
2.3.1 Reason for rotation
Clearly, assigning the priority of the balance tree Treap with the random number function rand() does not guarantee the nature of the small root heap, that is, node A may have a higher priority number than its child nodes.
In order to maintain the nature of the small root heap, Treap must be rotated left and right.
2.3.2 Rule of Rotation
So when should I turn left and when should I turn right?
Let's study the figure above first.In the figure, 3 is rotated to the left, and 4 replaces the original position of 3 after rotation.
The answer is clear.Because the priority of 3 (i.e. 30) is larger than that of 4 (i.e. 15), it does not have the nature of a small root heap, so it is left-handed.
Generally speaking, this summarizes when to rotate left and when to rotate right:
A's right child has a higher priority than A's left-handed
A's left child has a higher priority than A's right hand
2.3.3 Rotation Process
2.3.3.1 Left Rotation
-
The left child of A becomes the right child of the left child of A;
-
A The value of the left child's right child becomes the value of A;
-
The value of A becomes the value of the left child of A.
2.3.3.2 Right Hand
-
The right child of A becomes the left child of the right child of A;
-
A The value of the right child's left child becomes the value of A;
-
The value of A becomes the value of the right child of A;
2.3.3.3 Summary
Obviously, left-handed and right-handed operations are the exact opposite.
Taken together 2.2 and 2.3, we can get the code for the rotation and insertion operations
1 void Zig(int &p) //Right Hand 2 { 3 int q=t[p].l; 4 t[p].l=t[q].r; 5 t[q].r=p; 6 p=q; 7 Update(t[p].r); //Get Right Child's Size 8 Update(p); //Update because location was updated p Of Size 9 } 10 void Zag(int &p) //Left-handed 11 { 12 int q=t[p].r; 13 t[p].r=t[q].l; 14 t[q].l=p; 15 p=q; 16 Update(t[p].l); //Get Right Child's Size 17 Update(p); //Ditto 18 } 19 void Insert(int &p,int val) 20 { 21 if(p==0) //Node does not exist and has found its proper location 22 { 23 p=Get_New(val); 24 return ; 25 } 26 if(val==t[p].val) 27 { 28 t[p].num++; //Node already exists 29 Update(p); //Of its own Size 30 return ; 31 } 32 if(val<t[p].val) //The key code of the current node is too large 33 { 34 Insert(t[p].l,val); //Find the right place to the left 35 if(t[p].data<t[t[p].l].data) 36 Zig(p); //rotate 37 } 38 else 39 { 40 Insert(t[p].r,val); //Find the right place 41 if(t[p].data<t[t[p].r].data) 42 Zag(p); //rotate 43 } 44 Update(p); //To update p Of Size 45 }
2.4 Delete
This operation is the operation in the original topic 22
Deleting a node is not that easy for a tree.
If the leaf node needs to be deleted, then it is more convenient, just delete the node.
If the node you want to delete now has children, it is more troublesome and needs to be dealt with.
Of course, like insertion, deletion is done recursively.
2.4.1 Process
Then there are the following processes:
-
If the node corresponding to the key to be deleted does not exist, it is returned directly.
-
If the node is found
-
If the number of copies of this node is more than 1, subtract it from the number of copies
-
If the node has a child node, that is, it is not a leaf node: if the priority of the left node is greater than that of the right node, or if there is no right node, turn right.Because right-hand rotation allows the left node to replace itself (see 2.32.3).Then delete the value of the right node of the left node (that is, the right node after right-handing).If the opposite is true, do the opposite.
-
Then the node is a leaf node and is deleted directly.
-
-
Not found
-
If the current key is larger than the one you are looking for, look to the left.
-
If the current key is smaller than the one you are looking for, look to the right.
-
2.4.2 Code
Code is derived from the above process:
1 void Remove(int &p,int val) 2 { 3 if(p==0) return ; 4 if(val==t[p].val) 5 { 6 if(t[p].num>1) 7 { 8 t[p].num--; 9 Update(p); 10 return ; 11 } 12 if(t[p].l||t[p].r) 13 { 14 if(t[p].r==0||t[t[p].l].data>t[t[p].r].data) 15 { 16 Zig(p); 17 Remove(t[p].r,val); 18 } 19 else 20 { 21 Zag(p); 22 Remove(t[p].l,val); 23 } 24 Update(p); 25 } 26 else p=0; 27 return ; 28 }
2.5 Ranking by Worth
Obviously, this kind of operation is to find rankings.
Therefore, this operation is based on a query.
2.5.1 Process
-
Return directly if the node does not exist
-
If found, return Size+1 of the left node
Why is that so?
Because all nodes of the left subtree of the node have smaller key codes than themselves, the largest subtree of the left node is its Size
So at this point, Size comes into play.
Also, because each node's key code of the right subtree of the node is larger than that of the node, it is not related to the rank of the node.
The Size of the left node is the number of left subtree nodes including the left node, which is also smaller than the key code of the node.
Just like no other number in a list is larger than him, and it ranks one, so add one.
-
If found, then the same routine:
-
If the current key is larger than the one you are looking for, look to the left.
-
If the current key is smaller than the one you are looking for, look to the right.
2.5.2 Code:
1 int Sortt(int &p,int val) 2 { 3 if(p==0) 4 return 0; 5 if(val==t[p].val) 6 return t[t[p].l].size+1; 7 if(val<t[p].val) 8 return Sortt(t[p].l,val); 9 return Sortt(t[p].r,val)+t[t[p].l].size+t[p].num; 10 }
2.6 Value from Rank
This operation, like 2.52.5, is query-based, but the query is not ranking, but the value of the node.
2.6.1 Process
Then, the process is also very good.
-
If the node does not exist, return the maximum value directly (note, not 0)
-
If the maximum number of subtree nodes of the left node is larger than the rank to be queried, look to the left.
Similarly, explain why:
It is known that the maximum number of subtree nodes of the left node is the number of nodes with small key codes of the current node, that is, its rank -1.
If the rank it is querying is lower than the rank it is currently, the key code of the current node is larger than the actual answer, so it queries the left node.
- If the sum of the maximum number of subtree nodes of the left node and the number of copies of the current node is larger than the rank to be queried, return your own key code.
Because if the rank it is querying is lower than it is now, you have already executed the second ifif statement, which is not going to happen.
So the rank you want to query is larger than the rank you have now, and the number of copies you have is smaller than the rank you have now.
So if ranking counts the number of replicas, the ranking to be queried is one of the rankings of all replicas of the current node.
So the node corresponding to this ranking is the current node or its copy.
Also, because the keys of the current node and its copy are equal, the keys of the current node are returned.
2.6.2 Process
1 int Value(int &p,int rank) 2 { 3 if(p==0) 4 return INT_MAX; 5 if(t[t[p].l].size>=rank) 6 return Value(t[p].l,rank); 7 if(t[t[p].l].size+t[p].num>=rank) 8 return t[p].val; 9 return Value(t[p].r,rank-t[t[p].l].size-t[p].num); 10 }
2.7 Seeking Forward
To be honest, it is the best understanding to seek precursors and successors.
Precursor: Defined as a number less than x and largest.
Generally speaking, the nearest x is smaller than it.
Not difficult to obtain, its main feature is smaller than x.
So:
2.7.1 Process
-
Find the left node of the current node first.
-
As long as there is a right node, look to the right.
Process 1 satisfies a smaller property than x, while process 2 satisfies the largest number.
2.7.2 Code
1 int Pre(int val) 2 { 3 int pre=1; 4 int p=root; 5 while(p) 6 { 7 if(val==t[p].val) 8 { 9 if(t[p].l>0) 10 { 11 p=t[p].l; 12 while(t[p].r>0) 13 p=t[p].r; 14 pre=p; 15 } 16 break; 17 } 18 if(t[p].val<val&&t[p].val>t[pre].val) pre=p; 19 if(val<t[p].val) 20 p=t[p].l; 21 else p=t[p].r; 22 } 23 return t[pre].val; 24 }
2.8 Succession
2.8.1 Process
Contrary to seeking precursors.
-
Find the right node of the current node first.
-
As long as there is a left node, look to the left.
Process 1 meets larger properties than x, while process 2 meets the minimum number.
2.8.2 Code
int Suf(int val) { int suf=2; int p=root; while(p) { if(val==t[p].val) { if(t[p].r>0) { p=t[p].r; while(t[p].l>0) p=t[p].l; suf=p; } break; } if(t[p].val>val&&t[p].val<t[suf].val) suf=p; if(val<t[p].val) p=t[p].l; else p=t[p].r; } return t[suf].val; }
2.9 main function
Reference Title Meaning:
int main() { std::ios::sync_with_stdio(false); //Input and output optimization Building(); cin>>m; while(m--) { int op,x; cin>>op>>x; if(op==1) { Insert(root,x); continue; } if(op==2) { Remove(root,x); continue; } if(op==3) { cout<<Sortt(root,x)-1<<endl; continue; } if(op==4) { cout<<Value(root,x+1)<<endl; continue; } if(op==5) { cout<<Pre(x)<<endl; continue; } if(op==6) { cout<<Suf(x)<<endl; continue; } } return 0; }
3 Code complete code:
I've explained it in detail, so it's clean and uncommented
1 #include<bits/stdc++.h> 2 #pragma GCC optimize(3) //Manual ozone suction 3 using namespace std; 4 struct Treap 5 { 6 int l,r,val,data,num,size; 7 }t[100005]; 8 int law,root,m; 9 int Get_New(int val) 10 { 11 ++law; 12 t[law].val=val; 13 t[law].data=rand(); 14 t[law].num=1; 15 t[law].size=1; 16 return law; 17 } 18 void Update(int &p) 19 { 20 t[p].size=t[t[p].l].size+t[t[p].r].size+t[p].num; 21 } 22 void Building() 23 { 24 Get_New(INT_MIN); 25 Get_New(INT_MAX); 26 root=1,t[1].r=2; 27 Update(root); 28 } 29 void Zig(int &p) 30 { 31 int q=t[p].l; 32 t[p].l=t[q].r; 33 t[q].r=p; 34 p=q; 35 Update(t[p].r); 36 Update(p); 37 } 38 void Zag(int &p) 39 { 40 int q=t[p].r; 41 t[p].r=t[q].l; 42 t[q].l=p; 43 p=q; 44 Update(t[p].l); 45 Update(p); 46 } 47 void Insert(int &p,int val) 48 { 49 if(p==0) 50 { 51 p=Get_New(val); 52 return ; 53 } 54 if(val==t[p].val) 55 { 56 t[p].num++; 57 Update(p); 58 return ; 59 } 60 if(val<t[p].val) 61 { 62 Insert(t[p].l,val); 63 if(t[p].data<t[t[p].l].data) 64 Zig(p); 65 } 66 else 67 { 68 Insert(t[p].r,val); 69 if(t[p].data<t[t[p].r].data) 70 Zag(p); 71 } 72 Update(p); 73 } 74 void Remove(int &p,int val) 75 { 76 if(p==0) return ; 77 if(val==t[p].val) 78 { 79 if(t[p].num>1) 80 { 81 t[p].num--; 82 Update(p); 83 return ; 84 } 85 if(t[p].l||t[p].r) 86 { 87 if(t[p].r==0||t[t[p].l].data>t[t[p].r].data) 88 { 89 Zig(p); 90 Remove(t[p].r,val); 91 } 92 else 93 { 94 Zag(p); 95 Remove(t[p].l,val); 96 } 97 Update(p); 98 } 99 else p=0; 100 return ; 101 } 102 if(val<t[p].val) 103 Remove(t[p].l,val); 104 else Remove(t[p].r,val); 105 Update(p); 106 } 107 int Sortt(int &p,int val) 108 { 109 if(p==0) 110 return 0; 111 if(val==t[p].val) 112 return t[t[p].l].size+1; 113 if(val<t[p].val) 114 return Sortt(t[p].l,val); 115 return Sortt(t[p].r,val)+t[t[p].l].size+t[p].num; 116 } 117 int Value(int &p,int rank) 118 { 119 if(p==0) 120 return INT_MAX; 121 if(t[t[p].l].size>=rank) 122 return Value(t[p].l,rank); 123 if(t[t[p].l].size+t[p].num>=rank) 124 return t[p].val; 125 return Value(t[p].r,rank-t[t[p].l].size-t[p].num); 126 } 127 int Pre(int val) 128 { 129 int pre=1; 130 int p=root; 131 while(p) 132 { 133 if(val==t[p].val) 134 { 135 if(t[p].l>0) 136 { 137 p=t[p].l; 138 while(t[p].r>0) 139 p=t[p].r; 140 pre=p; 141 } 142 break; 143 } 144 if(t[p].val<val&&t[p].val>t[pre].val) pre=p; 145 if(val<t[p].val) 146 p=t[p].l; 147 else p=t[p].r; 148 } 149 return t[pre].val; 150 } 151 int Suf(int val) 152 { 153 int suf=2; 154 int p=root; 155 while(p) 156 { 157 if(val==t[p].val) 158 { 159 if(t[p].r>0) 160 { 161 p=t[p].r; 162 while(t[p].l>0) 163 p=t[p].l; 164 suf=p; 165 } 166 break; 167 } 168 if(t[p].val>val&&t[p].val<t[suf].val) 169 suf=p; 170 if(val<t[p].val) 171 p=t[p].l; 172 else p=t[p].r; 173 } 174 return t[suf].val; 175 } 176 int main() 177 { 178 std::ios::sync_with_stdio(false); 179 Building(); 180 cin>>m; 181 while(m--) 182 { 183 int op,x; 184 cin>>op>>x; 185 if(op==1) 186 { 187 Insert(root,x); 188 continue; 189 } 190 if(op==2) 191 { 192 Remove(root,x); 193 continue; 194 } 195 if(op==3) 196 { 197 cout<<Sortt(root,x)-1<<endl; 198 continue; 199 } 200 if(op==4) 201 { 202 cout<<Value(root,x+1)<<endl; 203 continue; 204 } 205 if(op==5) 206 { 207 cout<<Pre(x)<<endl; 208 continue; 209 } 210 if(op==6) 211 { 212 cout<<Suf(x)<<endl; 213 continue; 214 } 215 } 216 return 0; 217 }
Four people summary
I hope you can get a lot from this blog. It took me more than a month to edit this blog.
If there are any deficiencies, consult you!!