Title Description:

Source: LeetCode
Link: https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof

• Given a binary search tree, please find the value of the k-largest node.

Example:

• Example 1:

input: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
 output: 4

• Example 2:

input: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
 output: 4

• Tips:

     1 ≤ k ≤ Number of binary search tree elements

Analytical train of thought 1: violent solution

• Using the queue, directly take out all nodes, put them into the container, sort them, and return the corresponding K value according to the index.

Code (python3)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        res = []
        queue = [root]  
        while queue:       # Jump out of loop when queue is empty
            node = queue.pop() # Delete this layer node
            res.append(node.val)
            if node.left: queue.append(node.left)  # If the node of the current layer has child nodes, it will be added to the queue for the next round of child node extraction
            if node.right: queue.append(node.right)
        res.sort()  # sort
        return res[-k]
        

Code (cpp)

Analytic idea 2: use the ergodic property of binary search tree (medium order ergodic + early return)

• Reference k-jdy-analysis.

• Through the different access order of the nodes of the tree, there are three traversals:

• Preorder: (root, left, right) first accesses the root node, then recursively accesses the left subtree in the preorder, and finally accesses the right subtree in the preorder.

• inorder: (left, root, right)

• Subsequent traversal: (left, right, root)
  

• The nature of binary search tree (BST): keys smaller than the parent node appear in the left subtree and keys larger than the parent node appear in the right subtree.

• Example:

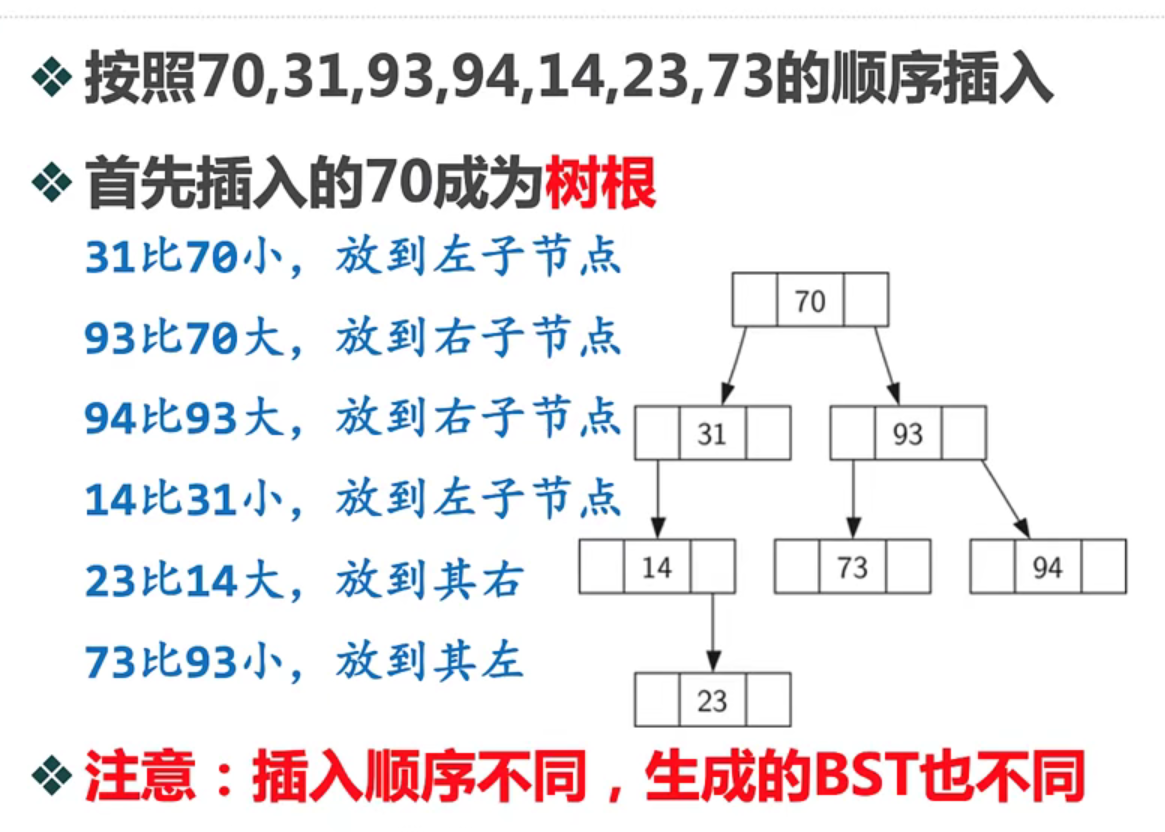
• Based on the properties of binary search tree, we can know that the middle order traversal (left, root and right) is an increasing sequence.

• Then, the middle order traversal reverse order of the binary search tree is a decreasing sequence.
  

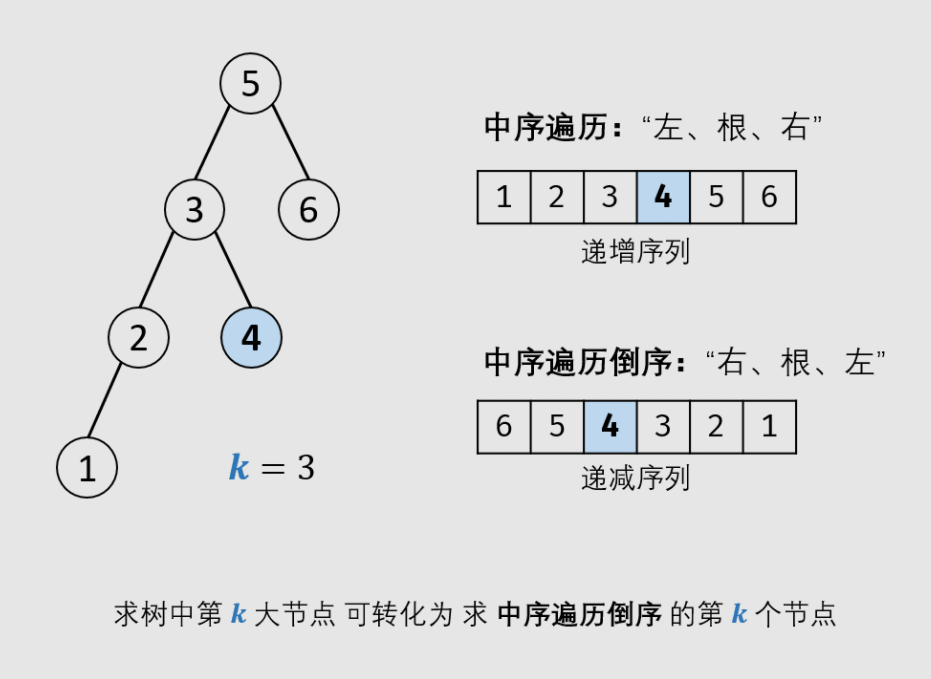
• Recursive code for middle order traversal of tree:

def inorder(root):
	if not root: return
	inorder(root.left)   # Access left
	print(root.val)      # Access root (medium)
	inorder(root.right)  # Access right

• Recursive code in reverse order of middle order traversal of tree:

def inorder(root):
	if not root: return
	inorder(root.right)  # Access right
	print(root.val)      # Access root (medium)
	inorder(root.left)   # Access left
	

• Find the node logic with the largest K in the tree node:
  1. Count during recursive traversal and count the serial number of the current node;

1. When recursing to the k th node, the result res shall be recorded;
2. After recording the results, the subsequent traversal will lose its meaning and should be terminated in advance (i.e. returned);
   

Schematic diagram of algorithm flow:

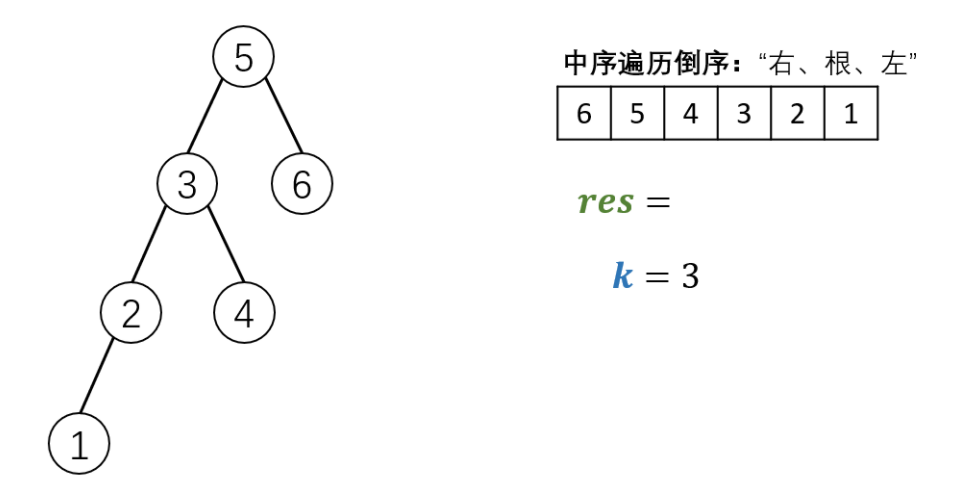
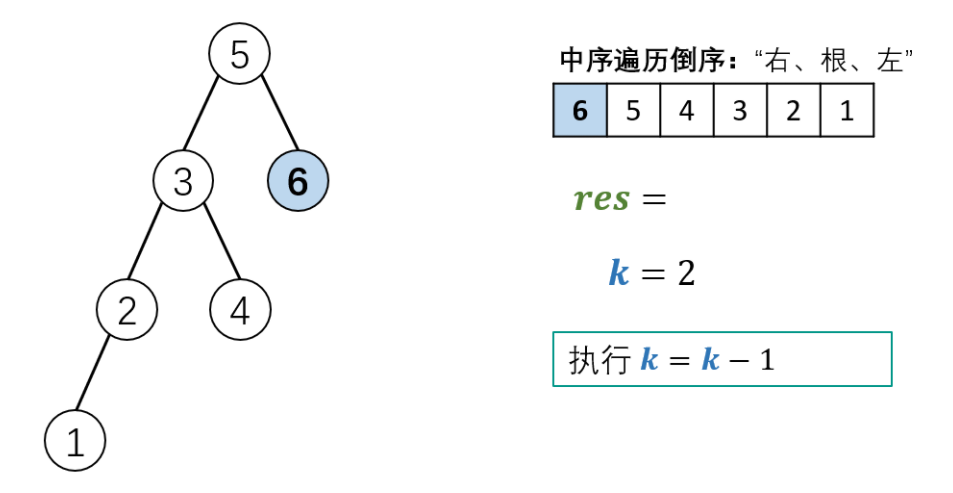
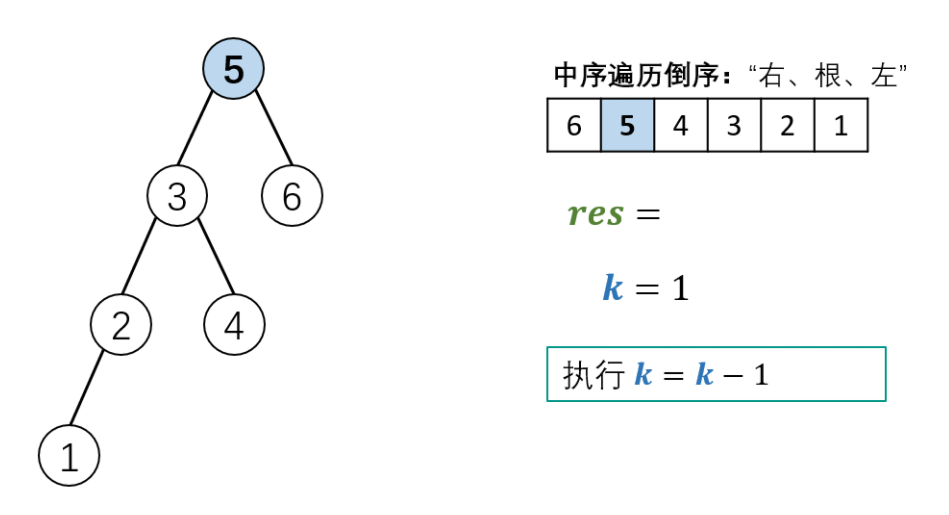
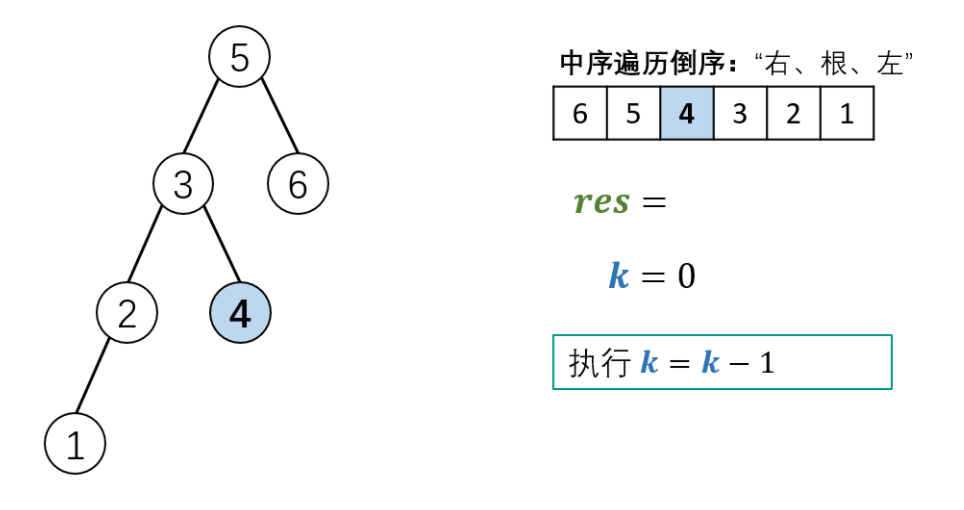
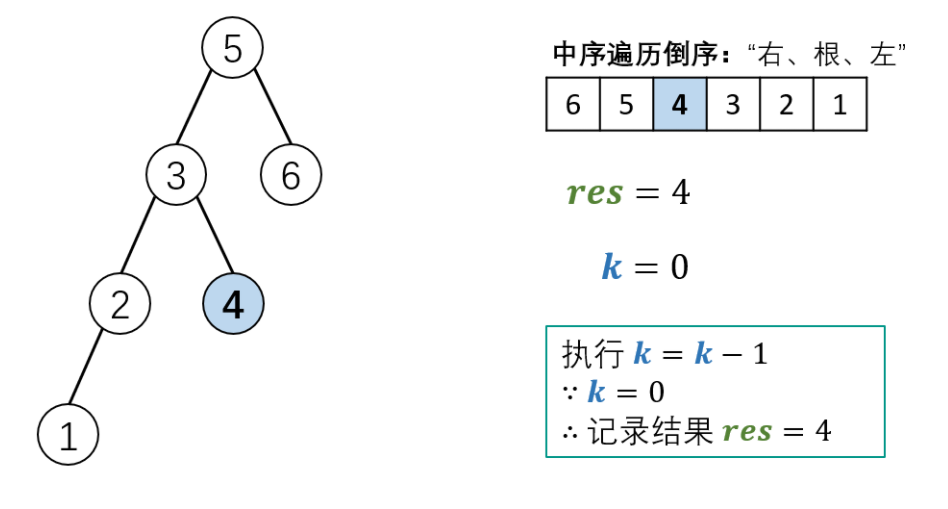
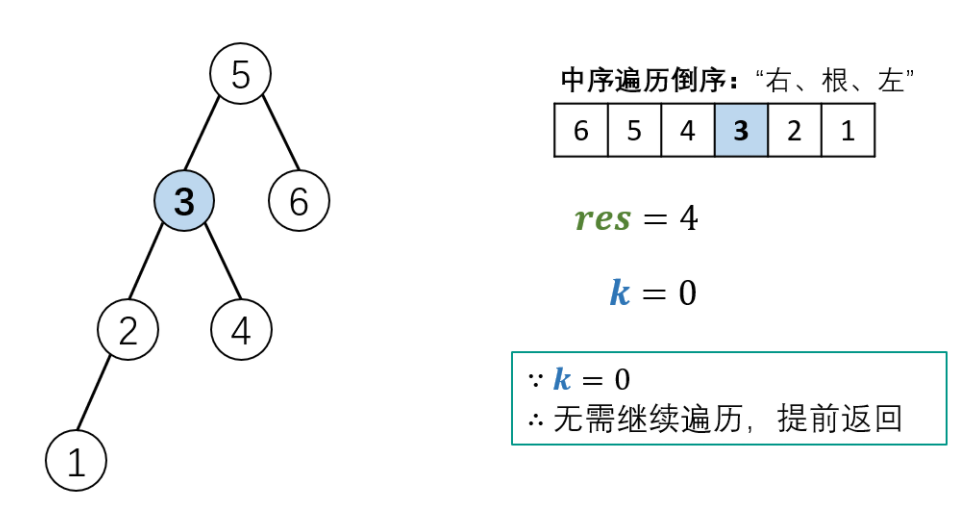
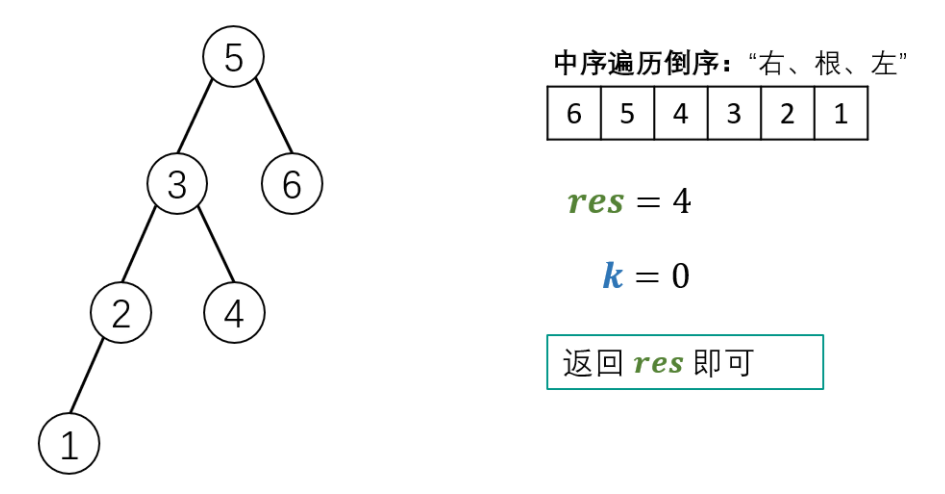
Code (python3)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def kthLargest(self, root: TreeNode, k: int) -> int:
        def reinorder(root):  # The formal parameter k cannot change with the iteration of the reinorder function
            if not root :return
            reinorder(root.right)  
            if self.k == 0: return   # Judge the largest first number in reverse order; Understanding (self.k): the reinorder function directly uses the formal parameter value k to initialize the variable
            self.k -=1     # The recursive index value K-1 is greater than 0
            if self.k == 0: self.res = root.val
            reinorder(root.left)
        self.k = k  # Initialize the class variable count with the formal parameter value k
        reinorder(root)
        return self.res
        

Code (cpp)

Ergodic reverse order

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
    
private:
    int res;
public:

    // Traversal of declaration tree in reverse order
    void reinorder(TreeNode* root,int & k){ // Reference passing makes all recursive functions share a k 
        if(!root) return;
        reinorder(root->right,k);  // Access right subtree node
        // if (k==0) return;  //  Early return
        k--;
        if (!k) res = root->val;  // Access root node
        reinorder(root->left,k);  // Access left subtree node
    }
    int kthLargest(TreeNode* root, int k) {
        reinorder(root,k);
        return res;
    }
};

Complexity analysis:

• Time complexity O(N): when the tree degenerates into a linked list (all right child nodes), the recursion depth is N regardless of the value of k, taking O(N) time.
• Space complexity O(N): when the tree degenerates into a linked list (all right child nodes), the system uses a stack space of O(N).