Sword finger Offer 07 Rebuild binary tree

Enter the results of preorder traversal and inorder traversal of a binary tree, please build the binary tree and return its root node.
It is assumed that the input pre order traversal and middle order traversal results do not contain duplicate numbers.

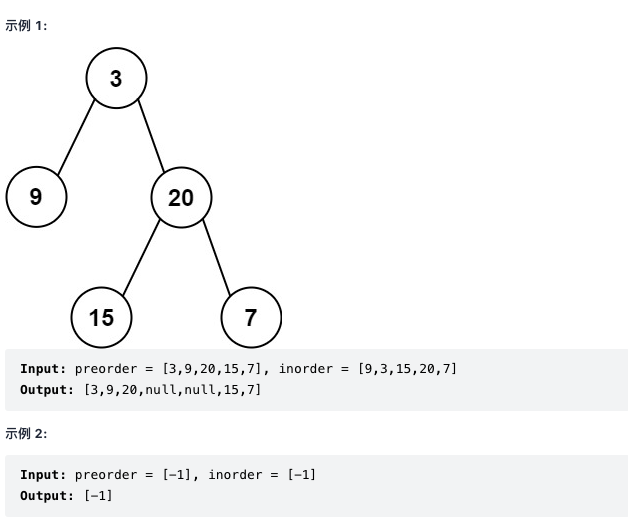
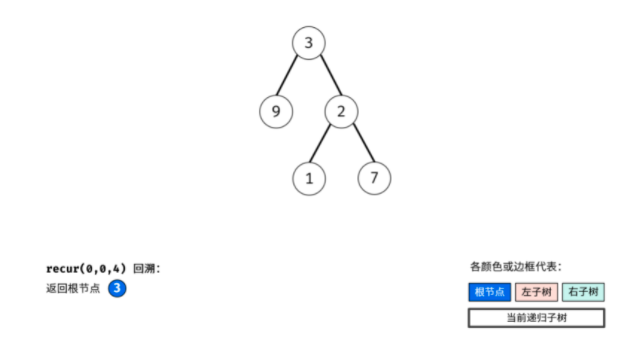
This problem uses the idea of recursion. Use pre to find the root and in to find the left and right subtrees. The following is the schematic diagram I drew. It's very nice.

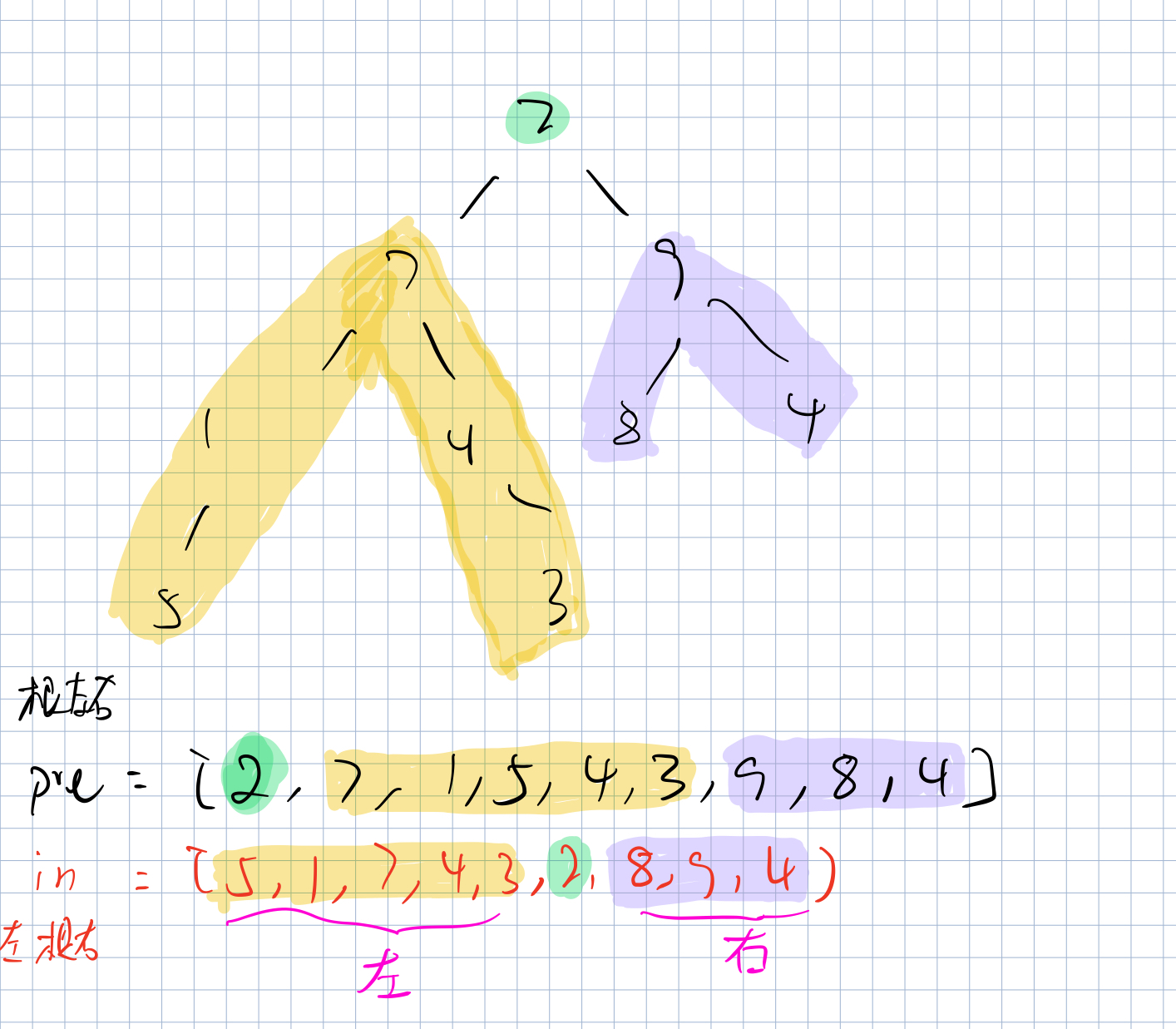
Look directly at the boss's ideas and code. I really can't think of it.


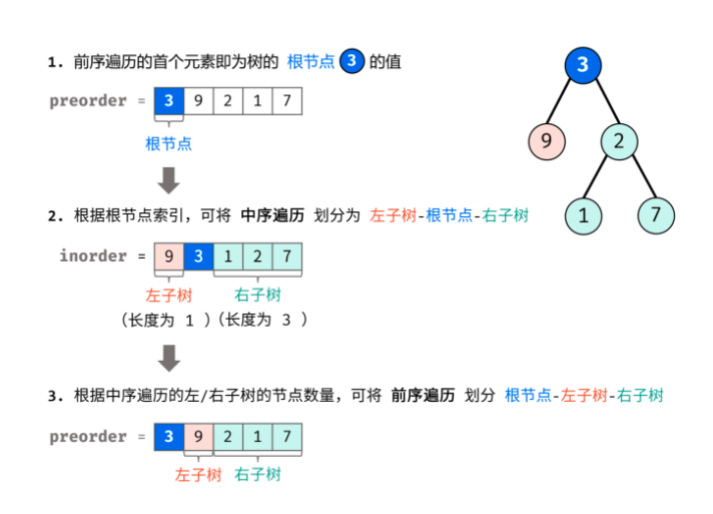
Through the above three steps, three nodes can be determined: 1 Root node of tree, 2 Left subtree root node, 3 The root node of the right subtree. (I didn't think about getting the roots of the left and right subtrees)

According to the idea of "divide and conquer algorithm", for the left and right subtrees of the tree, the above method can still be reused to divide the left and right subtrees of the subtree.













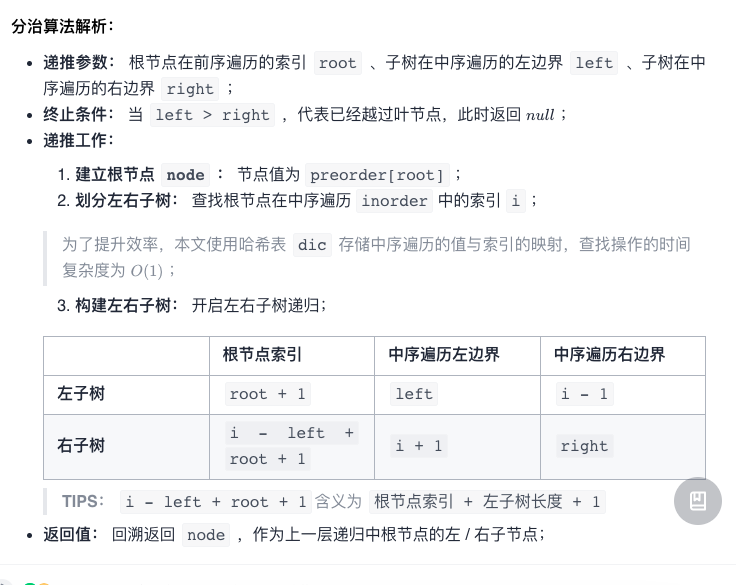
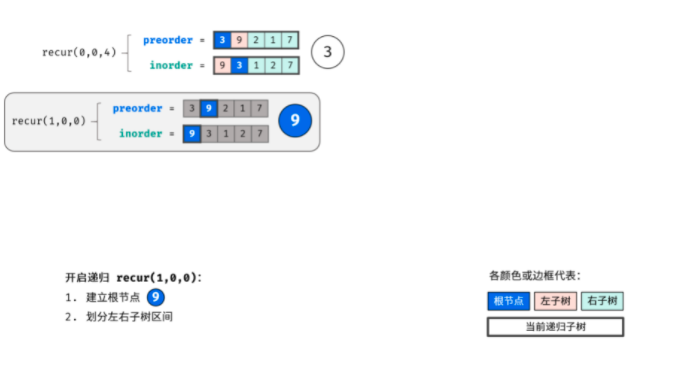
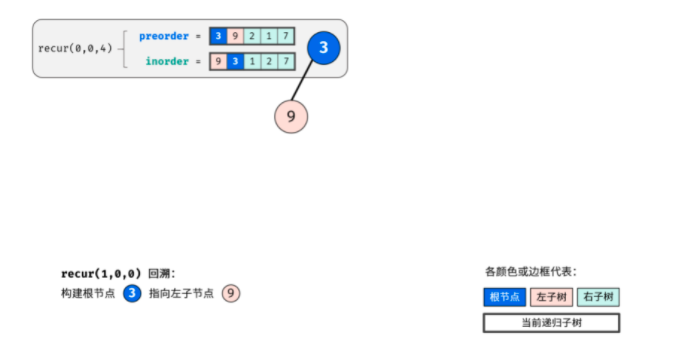
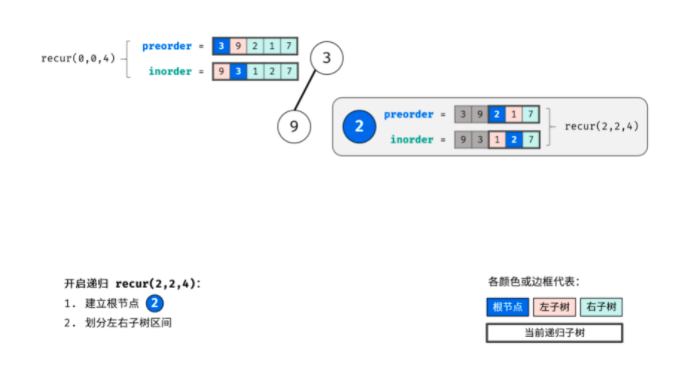
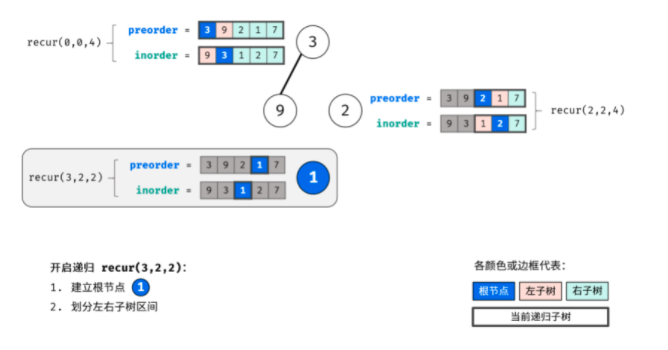
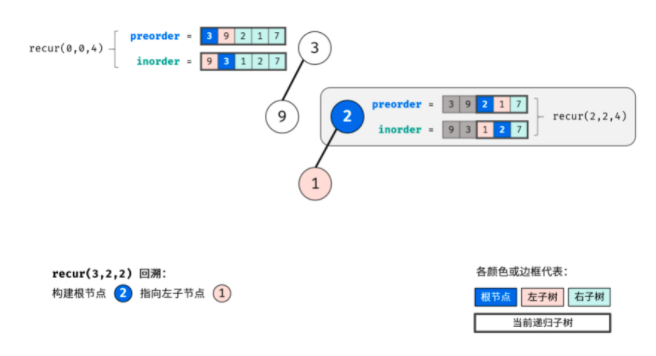
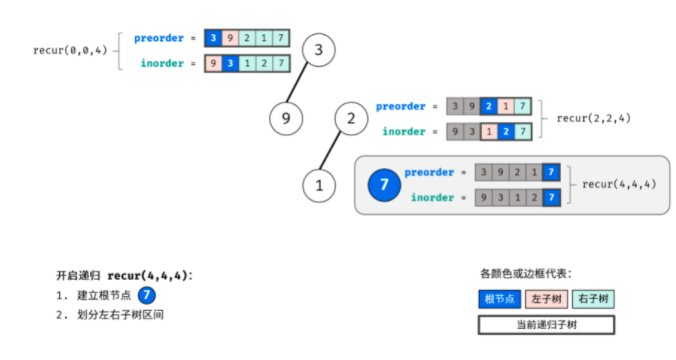
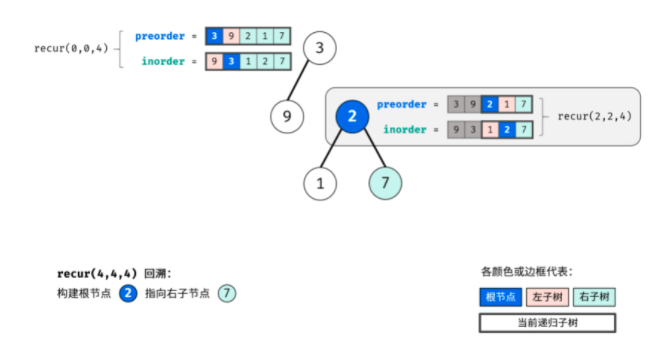
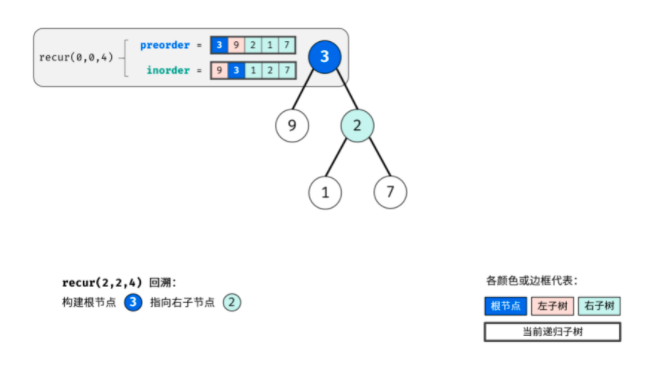
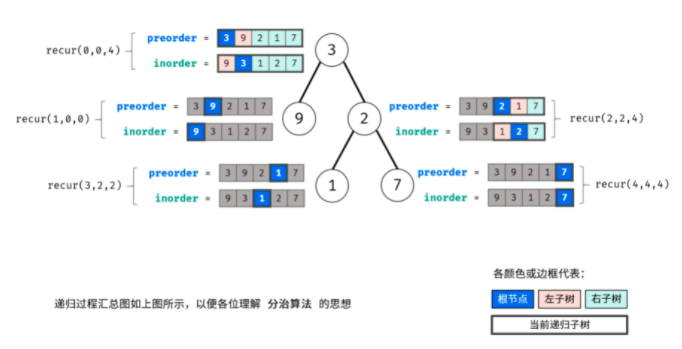
Boss Code:

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        def recur(root, left, right):
            if left > right: return                               # Recursive termination
            node = TreeNode(preorder[root])                       # Establish root node
            i = dic[preorder[root]]                               # Divide root node, left subtree and right subtree
            node.left = recur(root + 1, left, i - 1)              # Turn on left subtree recursion
            node.right = recur(i - left + root + 1, i + 1, right) # Turn on right subtree recursion
            return node                                           # Backtracking returns the root node

        dic, preorder = {}, preorder
        for i in range(len(inorder)):
            dic[inorder[i]] = i
        return recur(0, 0, len(inorder) - 1)

Sword finger Offer 16 Integer power of value

Realize pow(x, n), that is, calculate the N-power function of X (i.e., xn). Library functions must not be used and large numbers do not need to be considered.

I wrote my own violence law. The time is beyond the limit

def myPow(self, x: float, n: int) -> float:
        if n == 0: return 1
        res = x
        ite = abs(n) - 1
        for i in range(ite):
            res = res * x
        return res if n > 0 else 1 / res

In "40 lectures on algorithm clearance", Mr. TAN Chao talked about the method of one bit operation, but I can't remember clearly. Let me review my notes again.

Leetcode231: judge whether a number is to the power of 2.
1) Keep taking the film to see if it is 0 in the end
2) log2, see if it's an integer
3) Bit operation: judge that there is only one 1 and the rest are 0. X & (x-1) is the number of bits, moving one bit backward. Judge whether each bit is 0.

Here is the idea and code of the boss:



The code written according to the boss's idea still can't get through there:

def myPow(self, x: float, n: int) -> float:
        if n == 0: return 1
        pos = True
        if n < 0: 
            n = abs(n)
            pos = False
        res, a = 1, 1
        while n:
            if n & 1:
                res *= x**a
            n >>= 1
            a *= 2
        return res if pos else 1/res

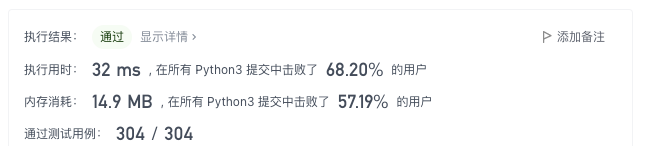
Here's the big guy's code:

class Solution:
    def myPow(self, x: float, n: int) -> float:
        if x == 0: return 0
        res = 1
        if n < 0: x, n = 1 / x, -n
        while n:
            if n & 1: res *= x
            x *= x
            n >>= 1
        return res

Sword finger Offer 33 Postorder traversal sequence of binary search tree

Enter an integer array to determine whether the array is the post order traversal result of a binary search tree. If yes, it returns true; otherwise, it returns false. Suppose that any two numbers of the input array are different from each other.


I didn't think of it. Just look at the boss's ideas and code.












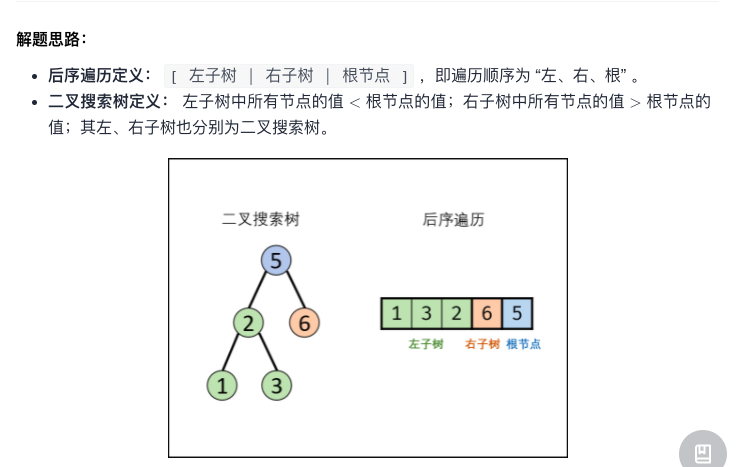
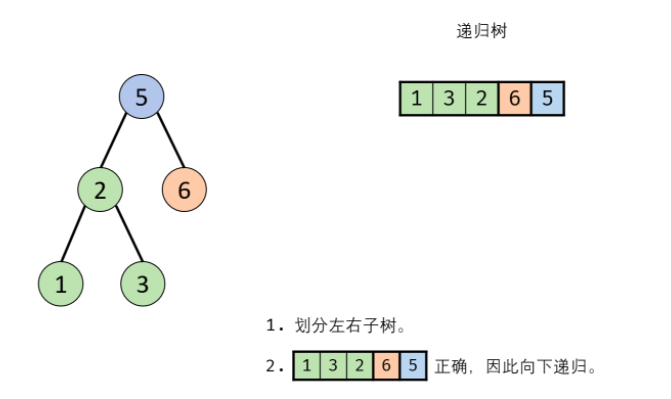
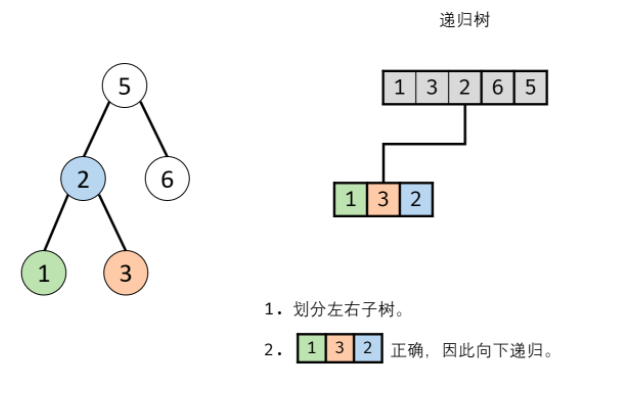
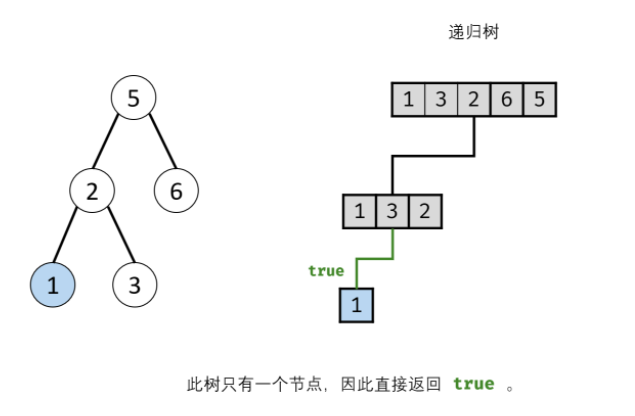
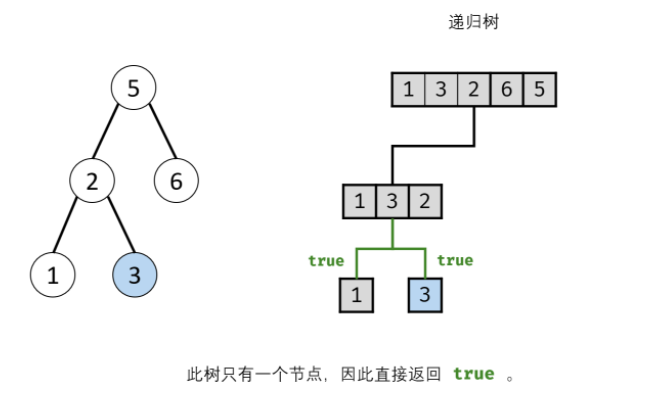
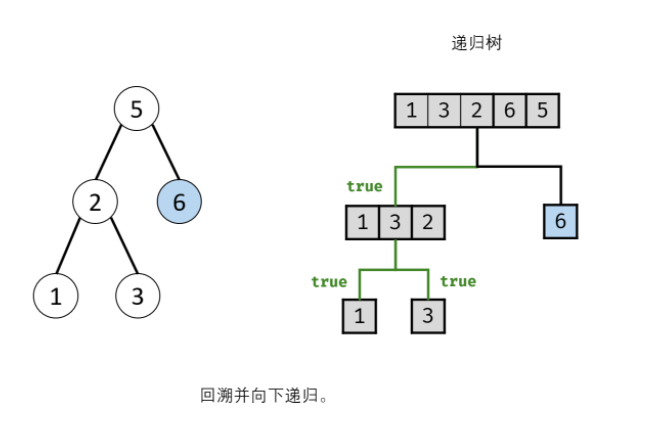
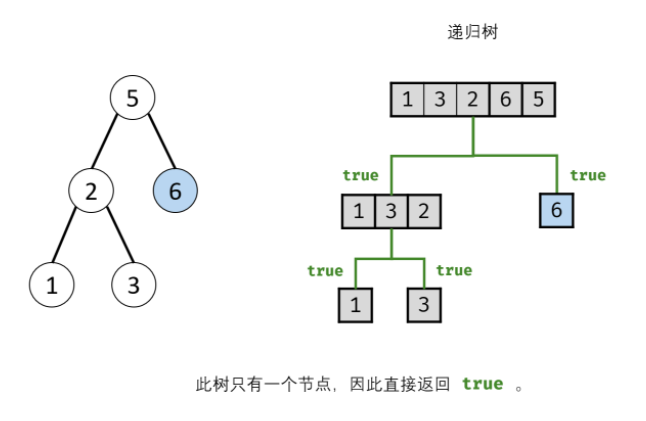
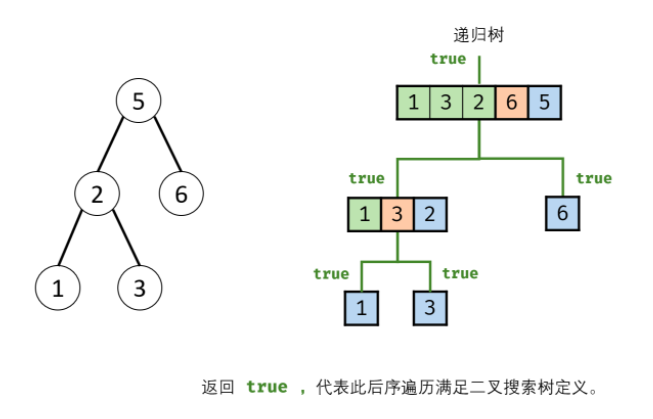
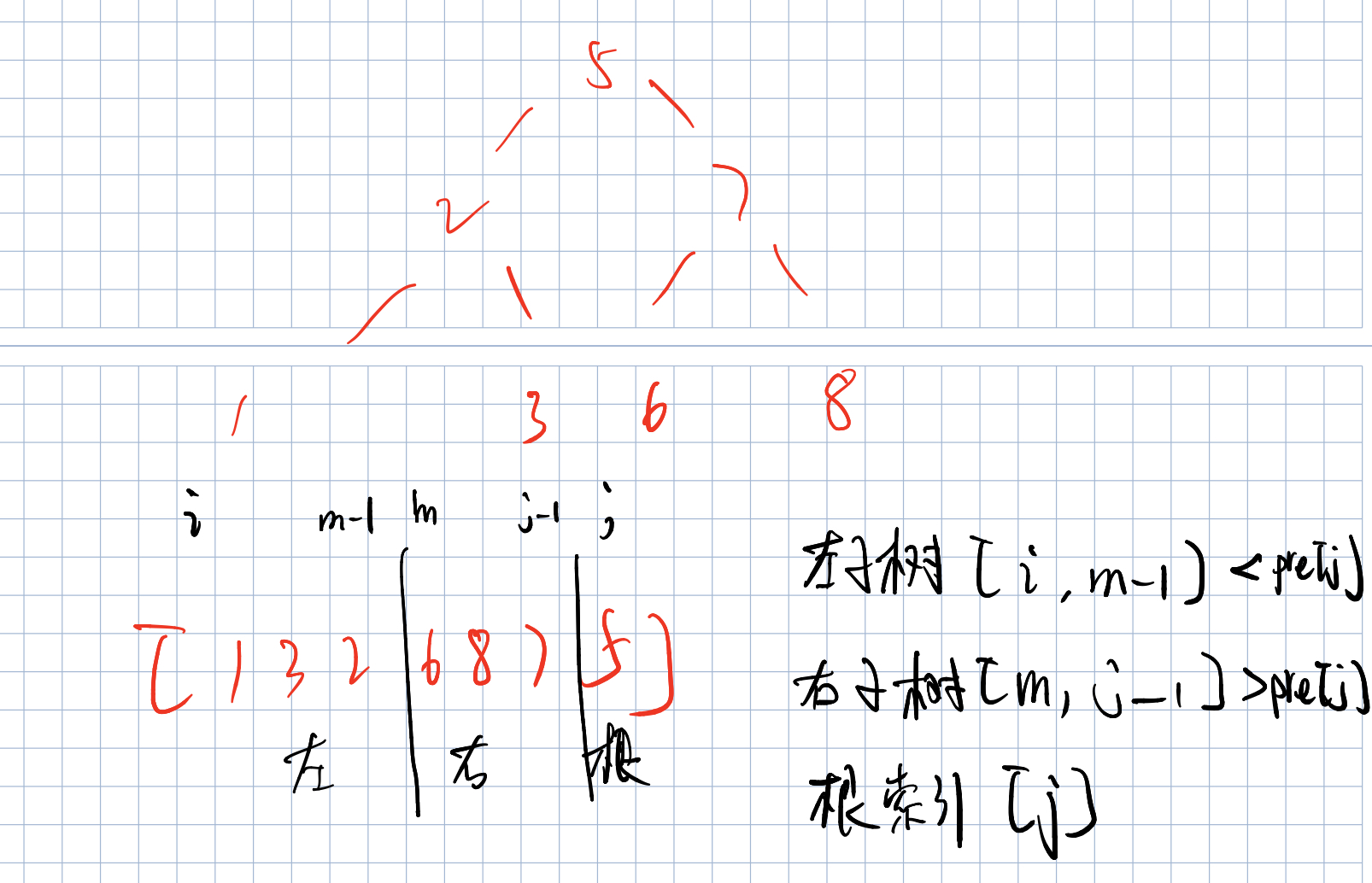
According to the idea of the boss, I tried to write, but I couldn't call recursion:

 def verifyPostorder(self, postorder: List[int]) -> bool:
        i, j = 0, len(postorder) - 1
        # Find the first straight index m larger than the root
        while i < j:
            if postorder[i] > postorder[j]:
                m, i = i, 0
                break
            i += 1
        else: return False
        for item in postorder[m:j-1]:
            if item < postorder[j]:
                return False
        return True
        self.verifyPostorder(postorder[i:m-1])
        self.verifyPostorder(postorder[m:j-1])

Here's the big guy's code:

class Solution:
    def verifyPostorder(self, postorder: [int]) -> bool:
        def recur(i, j):
            if i >= j: return True
            p = i
            while postorder[p] < postorder[j]: p += 1
            m = p
            while postorder[p] > postorder[j]: p += 1
            return p == j and recur(i, m - 1) and recur(m, j - 1)

        return recur(0, len(postorder) - 1)