1, Title Description

To define the data structure of the stack, please implement a min function that can get the smallest element of the stack in this type. In this stack, the time complexity of calling min, push and pop is all. O ( 1 ) \rm{O(1)} O(1).

Example:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();      --> return-3.
minStack.pop();
minStack.top();      --> Return 0.
minStack.min();      --> return-2.

Tips:
The total number of calls of each function shall not exceed 20000

2, Train of thought analysis

Note: some contents and pictures in the thought analysis refer to the predecessors. Thank them for their selfless dedication

analysis

The complexity of push() and pop() functions of ordinary stack is O(1), while the min() function to obtain the minimum value of stack needs to traverse the whole stack, and the complexity is O(N).
This problem needs to reduce the complexity of min() function to O(1), which can be realized by establishing auxiliary stack. Stack 1 is used to store all elements. push() function, pop() function and top() function at the top of stack remain normal. The smallest element of stack 1 is always placed on the top of stack 2, so that the O(1) complexity of min() function can be realized.

Function design

push(x) function
① Stack 1 can be put into the stack normally
② For stack 2, it should be noted that the top of stack 2 must be the smallest element of stack 1. Each time you enter the stack, judge whether stack 2 is empty. If it is empty, press X into stack 2. If stack 2 is not empty, judge the size relationship between X and the top element of stack 2. If x ≤ the top element of stack 2, press X into stack 2.
pop() function
① Stack 1 can exit the stack normally
② For stack 2, it should be noted that after stack 1 leaves stack 1 element, the top element of stack 2 should still be the smallest element of stack 1. Each time the stack is out, the out of stack element is marked as y. if y is equal to the top element of stack 2, stack 2 also performs out of stack
top() function
Directly return to the top element of stack 1
min() function
Directly return to the top element of stack 2
Example:

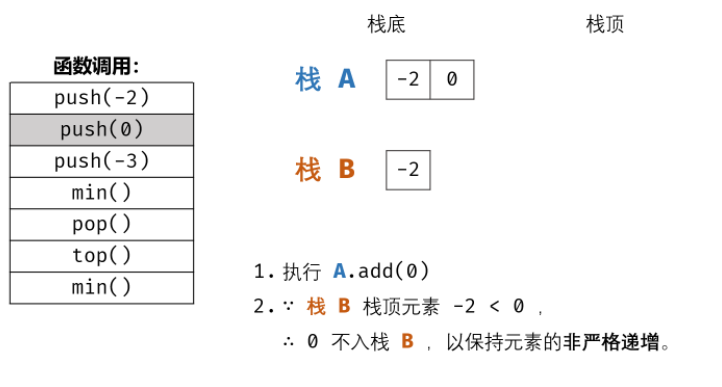
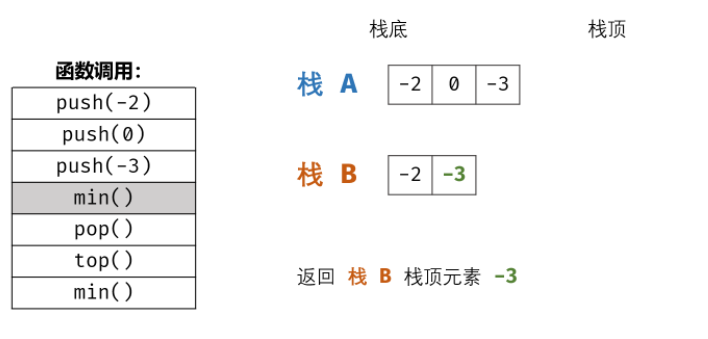
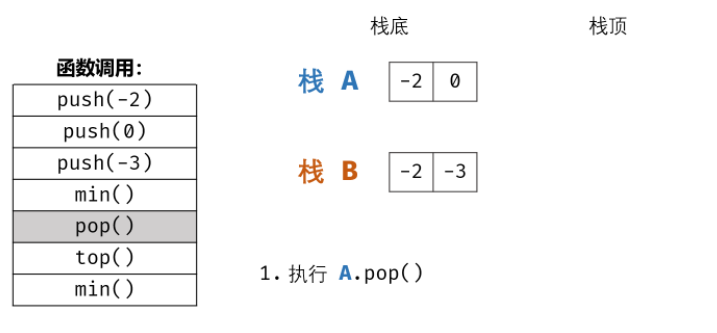
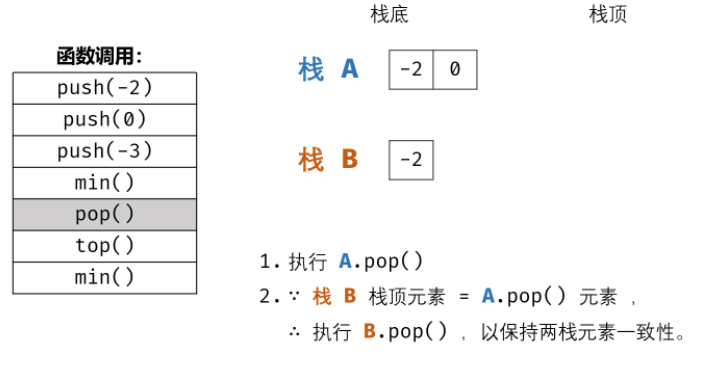
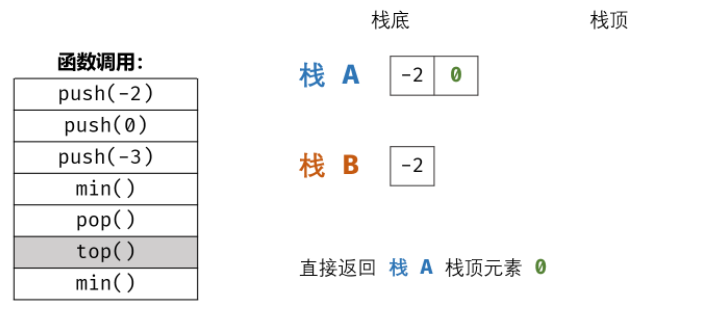
3, Overall code

The overall code is as follows

#define N 20000

//Create two stacks. Stack 1 is used for normal stack in and stack out operations, and stack 2 is used to prevent the smallest element of stack 1 from being on the top of the stack
typedef struct {
    int *Stack1;
    int *Stack2;
    int top1;
    int top2;
} MinStack;

/** initialize your data structure here. */

MinStack* minStackCreate() {
    MinStack* MS=(MinStack*)malloc(sizeof(MinStack));
    MS->Stack1 = (int*)malloc(sizeof(int)*N);
    MS->Stack2 = (int*)malloc(sizeof(int)*N);
    MS->top1 = -1;
    MS->top2 = -1;
    return MS;
}

void minStackPush(MinStack* obj, int x) {
    obj->Stack1[++obj->top1] = x; //Stack 1 enters the stack normally
    if(obj->top2 == -1){   //If stack 2 is empty
        obj->Stack2[++obj->top2] = x; //Push x into stack 2, too
    }
    else{
        //If stack 2 is not empty, and x < = stack top element of stack 2
        if(x <= obj->Stack2[obj->top2]){
            //Press x into the top of stack 2
            obj->Stack2[++obj->top2] = x;
        }
    }

}

void minStackPop(MinStack* obj) {
    //Save the top element of stack 1, and top 1-1
    int a = obj->Stack1[obj->top1];
    obj->top1--;
    //If the top element of stack 1 is equal to the top element of stack 2, pop up the top element of stack 2, top2-1
    if(a==obj->Stack2[obj->top2]){
        obj->top2--;
    }
}

//Return to the top element of stack 1 normally
int minStackTop(MinStack* obj) {
    return obj->Stack1[obj->top1];
}

//Return to the top element of stack 2 normally
int minStackMin(MinStack* obj) {
    return obj->Stack2[obj->top2];
}

void minStackFree(MinStack* obj) {
    free(obj->Stack1);
    free(obj->Stack2);
    free(obj);
}

/**
 * Your MinStack struct will be instantiated and called as such:
 * MinStack* obj = minStackCreate();
 * minStackPush(obj, x);
 
 * minStackPop(obj);
 
 * int param_3 = minStackTop(obj);
 
 * int param_4 = minStackMin(obj);
 
 * minStackFree(obj);
*/

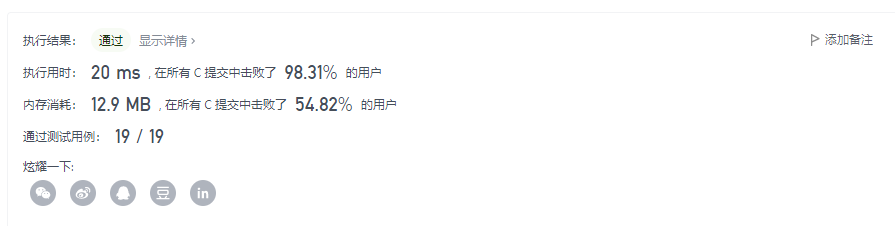
Run and verify