Date: 2019-08-14
1. The entry node of the link in the list (inspecting knowledge points: list)
Topic Description
Give a linked list, if it contains a ring, please find the entry node of the ring of the linked list, otherwise, output null.
Analysis: In the first case, without considering the time complexity, we can use a list to store elements traversing the ring list directly. This time complexity is O(N). In storage, if the element is already in the list, it indicates the entrance to the ring list. Otherwise, continue walking backwards.
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
if not pHead:
return None
p = pHead
reslist = []
while p:
if p in reslist:
return p
else:
reslist.append(p)
p = p.nextThe second way of thinking comes from the idea of offer ing by sword finger:
If there are n nodes in the link list, pointer P1 moves forward n steps on the list, and then the two pointers move forward at the same speed. When the second pointer points to the entry node of the ring, the first pointer has circled around the ring and returned to the entry node. But first we need to get the number of nodes in the ring. The idea of calculating the number is that the node that meets above must be in the ring, so we can start from this node and continue to move forward while counting. The next time we return to this node, we can get the number of rings.
Specifically:
- The first step is to find the intersection point in the ring. Point P1 and P2 at the head of the list, P1 takes one step at a time and P2 takes two steps at a time until p1==p2 finds the intersection point in the ring.
- The second step is to find the entrance of the ring. Next step, when p1= p2, P2 passes through 2x, p1 passes through x, suppose there are n nodes in the ring, P2 goes around 2x = n + X more than p1; n = x; we can see that P1 actually takes a step of a ring, and then P2 points to the head of the list, P1 position remains unchanged, p1,p2 goes one step at a time until p1= p2; at this time P1 points to the entrance of the ring.
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
# Judgment of preconditions
if not pHead or not pHead.next or not pHead.next.next:
return None
# Let the slow pointer take one step at a time, and the fast pointer take two steps at a time. The first encounter must be in the ring. When meeting: Slow down x, then fast walk 2x = x + n (block actually takes an additional number of rings), so the slow pointer takes n steps altogether.
low = pHead.next
fast = pHead.next.next
while low != fast:
if not low or not fast:
return None
low = low.next
fast = fast.next.next
# When we meet, the slow pointer has already taken several steps in the ring, then let the fast pointer start from the beginning. Each time the two pointers take one step, the next encounter must be at the entrance node of the ring.
fast = pHead
while low != fast:
low = low.next
fast = fast.next
return fast2. Delete duplicate nodes in the linked list (inspect knowledge points: linked list)
Topic Description
In a sorted list, there are duplicate nodes. Please delete the duplicate nodes in the list. The duplicate nodes are not reserved and return to the header pointer of the list. For example, the chain table 1 - > 2 - > 3 - > 3 - > 4 - > 4 - > 5 is treated with 1 - > 2 - > 5.
The first idea is non-recursive deletion.
1. First, add a header node to facilitate the first node and the second node in the same situation.
2. Set up the pre, nex pointer, the pre pointer points to the node that is not duplicated currently, and the nex pointer is equivalent to the working pointer. Search backwards, delete the pointer that is duplicated with the current pre, and finally remember to delete the pre pointer in the current loop!
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def deleteDuplication(self, pHead):
# write code here
# First of all, judge the preconditions.
if pHead == None or pHead.next == None:
return pHead
# Establish a new node to facilitate subsequent iterations
new_head = ListNode(-1)
new_head.next = pHead
pre = new_head # Set the new node to pre
p = pHead # Nodes that need to be judged whether they are duplicated or not need to be updated
nex = None # Initialize the next node
while p != None and p.next != None: # When p is not empty, the next node of p is not empty either. Set nex or return to the end directly.
nex = p.next
if p.val == nex.val: # This if statement first fixes p, then judges the value of nex and p, if deletes nex equally, then searches continuously for repeated nex, and finally does not satisfy jumping out of the while statement for updating.
while nex != None and nex.val == p.val:
nex = nex.next
pre.next = nex
p = nex
else: # If the values of p and nex are different, pre and p traverse downward to make a judgment.
pre = p
p = p.next
return new_head.next # Because new_head is a new header node, it returns its next node
The second way of thinking: Recursive thinking that some people use on cattle passengers: (time complexity is higher, after all, recursion)
class Solution:
def deleteDuplication(self, pHead):
# write code here
# Precondition
if pHead is None or pHead.next is None:
return pHead
head1 = pHead.next
if head1.val != pHead.val: # If the values of two nodes are not equal, the judgement is called recursively down
pHead.next = self.deleteDuplication(pHead.next)
else:
while pHead.val == head1.val and head1.next is not None: # Otherwise, if head1.next is equal and not empty, delete head1 and loop while
head1 = head1.next
if head1.val != pHead.val: # When the deletion node terminates and the nodes are unequal, the subsequent nodes of head1 are judged recursively.
pHead = self.deleteDuplication(head1)
else:
return None
return pHead3. Next node of binary tree (inspecting knowledge point: tree)
Topic Description
Given a binary tree and one of its nodes, find the next node in the middle traversal order and return. Note that the nodes in the tree contain not only left and right child nodes, but also pointers to the parent node.
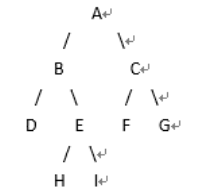
Ideas:
(1) If the node has a right subtree, the next node is the left-most subtree of the right subtree (as shown in Node B)
(2) If the node does not have a right subtree, there are two cases:
2.1 If the node is the left child of the parent, the next node is its parent (as shown in node D)
2.2 If the node is the right child of the parent node, it traverses upwards along the parent node until the left child of the parent node of a node is found to be the node, then the next node of the parent node of the node (as shown in Node I, B is the left child of the parent node) is found upwards along the parent node. Then the parent node A of B is the next node. The second scenario can be considered comprehensively.
# -*- coding:utf-8 -*-
# class TreeLinkNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# self.next = None
class Solution:
def GetNext(self, pNode):
# write code here
if pNode.right: #There are right subtrees
p=pNode.right
while p.left:
p=p.left
return p
while pNode.next: #If there is no right subtree, the first current node is the left child of the parent node.
if(pNode.next.left==pNode): # If the first if is set up, it indicates that it is the left child of the parent node and returns to the parent node.
return pNode.next
pNode = pNode.next #Otherwise, traverse up the parent node
return None #If the root node is not found, it returns empty.4. Symmetrical Binary Trees (Examining Knowledge Points: Trees)
Topic Description
Please implement a function to determine whether a binary tree is symmetrical. Note that if a binary tree has the same mirror image as the binary tree, it is defined as symmetric.
Analysis: There are many different processing details, some directly adopt the idea of recursion, some are to assign a tree, and then the left and right subtrees are traversed equally.
What I am using here is to go straight down and make gradual comparisons. First of all, four situations need to be judged:
The root is empty, True;
The left subtree is empty, the right subtree is not empty, False
Left subtree is not empty, right subtree is empty, False
Both left and right subtrees are empty, True
Finally, we recursively traverse the case that the left and right subtrees are not empty, and compare the values.
# -*- coding:utf-8 - * - My code, but did not pass, thinking and the latter version of the code is the same, doubtful. Is it the use of subfunctions?
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetrical(self, pRoot):
# write code here
if not pRoot:
return True
if not pRoot.left and not pRoot.right:
return True
if pRoot.left and not pRoot.right:
return False
if not pRoot.left and pRoot.right:
return False
while pRoot.left and pRoot.right:
if pRoot.left.val == pRoot.right.val:
return self.isSymmetrical(pRoot.left) and self.isSymmetrical(pRoot.right)
return False
return True
# -*- coding:utf-8 -*- # Code passed
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetrical(self, pRoot):
# write code here
def is_same(p1,p2):
if not p1 and not p2: # Both left and right subtrees are empty, True
return True
if (p1 and p2) and p1.val==p2.val: # Neither left nor right subtrees are empty, and the values are equal.
return is_same(p1.left,p2.right) and is_same(p1.right,p2.left)
return False
if not pRoot: # The roots are empty, True
return True
if pRoot.left and not pRoot.right: # The left subtree is not empty, the right subtree is empty, False
return False
if not pRoot.left and pRoot.right: # Right subtree is not empty, left subtree is empty, False
return False
return is_same(pRoot.left,pRoot.right) # Otherwise, recursive calls5. Print binary trees in zigzag order (inspecting knowledge points: stack + tree)
Topic Description
Please implement a function to print the binary tree in zigzag, that is, the first line is printed in left-to-right order, the second layer is printed in right-to-left order, the third line is printed in left-to-right order, and so on.
Analysis:
* Many of our implementations are to store data from each layer in ArrayList and perform reverse operations on even layers. But it's too inefficient when there's a lot of data.
If an interview is conducted, the algorithmic test is to print a zigzag binary tree, and use reverse, it will be despised. The interviewer will say that the efficiency of mass data is not at all good.
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def Print(self, pRoot):
# write code here
root=pRoot
if not root:
return []
level=[root]
result=[]
lefttoright=False # Marker, to determine whether to False from left to right or True from right to left
while level:
curvalues=[] # Current values, generally from left to right
nextlevel=[] # The node record in this layer, left node + right node
for i in level:
curvalues.append(i.val)
if i.left:
nextlevel.append(i.left)
if i.right:
nextlevel.append(i.right)
if lefttoright:
curvalues.reverse() # The first floor is from left to right False, and the next floor is from right to left True.
if curvalues:
result.append(curvalues) # Put the layer values in the correct order into the final result
level=nextlevel # level updates used in loops
lefttoright=not lefttoright # Changes in markers
return resultOther methods: instead of using reverse to change the order of storage first, they are in place one step at a time:
'''Solution: Use a flag variable to mark left-to-right or right-to-right If you go from left to right, traverse the node current_nodes at the current level from beginning to end, then append the left child and the right child to a list new_nodes, respectively. If you go from right to front, you traverse the current_nodes of the current layer from end to end, and insert the right child and the left child into a list new_nodes, respectively. The resulting new_nodes are also left-to-right ordered''
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def Print(self, pRoot):
# write code here
if pRoot == None:
return []
falg = 0 # 0 means left to right, 1 means right to left
node_list = [[pRoot]]
result = []
while node_list:
current_nodes = node_list[0] # Nodes in the current layer
node_list = node_list[1:]
new_nodes = [] # Next-tier nodes are stored in left-to-right order
res = [] # Output from the current layer
while len(current_nodes) > 0:
# From left to right
if falg == 0:
res.append(current_nodes[0].val)
if current_nodes[0].left != None:
new_nodes.append(current_nodes[0].left)
if current_nodes[0].right != None:
new_nodes.append(current_nodes[0].right)
current_nodes = current_nodes[1:]
# From right to left
else:
res.append(current_nodes[-1].val)
if current_nodes[-1].right != None:
new_nodes.insert(0, current_nodes[-1].right)
if current_nodes[-1].left != None:
new_nodes.insert(0, current_nodes[-1].left)
current_nodes = current_nodes[:-1]
result.append(res)
falg = 1 - falg
if new_nodes:
node_list.append(new_nodes)
return result6. Print the binary tree into multiple rows (inspect knowledge points: tree + queue)
Topic Description
Print the binary tree layer by layer from top to bottom, and output the same layer node from left to right. Each layer outputs one line.
Analysis: This problem is simpler than the previous one. The first implementation is as follows: Store the node value from left to right and the node of left and right children of each node from left to right directly from top to bottom.
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# Returns a two-dimensional list [[1,2], [4,5]]
def Print(self, pRoot):
# write code here
if pRoot == None:
return []
node_list = [[pRoot]]
result = [] # The values of nodes at each level are written as a list from left to right
while node_list:
current_nodes = node_list[0] # Each time the first value is taken as the order of nodes from left to right in the current layer, the nodes in the current layer
node_list = node_list[1:] # After that, node_list will delete and update the first value.
new_nodes = [] # Next-tier nodes are stored in left-to-right order
res = [] # The value of the current layer node is output in left-to-right order
while len(current_nodes) > 0:
res.append(current_nodes[0].val) # Store the value of a node in res
if current_nodes[0].left != None: #The left and right child nodes of the node store current_nodes in sequence
new_nodes.append(current_nodes[0].left)
if current_nodes[0].right != None:
new_nodes.append(current_nodes[0].right)
current_nodes = current_nodes[1:] # Delete and update of current node
result.append(res)
if new_nodes:
node_list.append(new_nodes)
return resultA more concise implementation is to initialize two lists and use res as the maximum list for storing the row value of each row node. tmp is used to store continuously updated current nodes.
1. First, update and store the row value of each row node, and save it in res.
2. Then update the TMP of the node in the layer: delete the node in the layer (from left to right), and get the node of the left and right children into the tmp. [Note: There is only a len(tmp) loop for the number of nodes in this layer: delete and update]
# -*- coding:utf-8 -*- # Personal support for this, easy to understand
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# Returns a two-dimensional list [[1,2], [4,5]]
def Print(self, pRoot):
# write code here
if not pRoot: # If the root node is empty, the final result is also empty.
return []
res = [] # A large list for storing row s of node values at each level
tmp = [pRoot] # Nodes used to store the current layer, in left-to-right order
while tmp:
row = [] # Storage of node values at the layer to form a small list
for i in tmp:
row.append(i.val)
res.append(row) # After storing the node value of the layer, the tmp of the node storing the layer is deleted and updated.
for i in range(len(tmp)):
t = tmp.pop(0) # Delete the node from left to right while storing the left and right child nodes of the node
if t.left:
tmp.append(t.left)
if t.right:
tmp.append(t.right)
return res
7. Serialized Binary Tree (Queue + Tree for Knowledge Points)
Topic Description
Please implement two functions to serialize and deserialize the binary tree, respectively
The serialization of binary tree means that a binary tree is saved as a string in a certain format according to the result of a certain traversal way, so that the binary tree built in memory can be persisted. Serialization can be modified by binary tree traversal based on order, middle order, post order and sequence. The result of serialization is a string. When serialization, empty nodes (#) are represented by some symbol. Represents the end of a node value.
Deserialization of a binary tree is to reconstruct a binary tree based on the result str of a serialized string obtained in a certain traversal order.