catalogue
Sword finger Offer II 013 Sum of two-dimensional submatrix
Sword finger Offer II 014 Anagrams in strings
Sword finger Offer II 015 All modifiers in the string
Sword finger Offer II 017 Shortest string containing all characters ☆
Sword finger Offer II 018 Valid palindrome
Sword finger Offer II 019 Delete at most one character to get a palindrome
Sword finger Offer II 020 Number of palindrome substrings
Sword finger Offer II 021 Delete the penultimate node of the linked list
2, 013 - 026
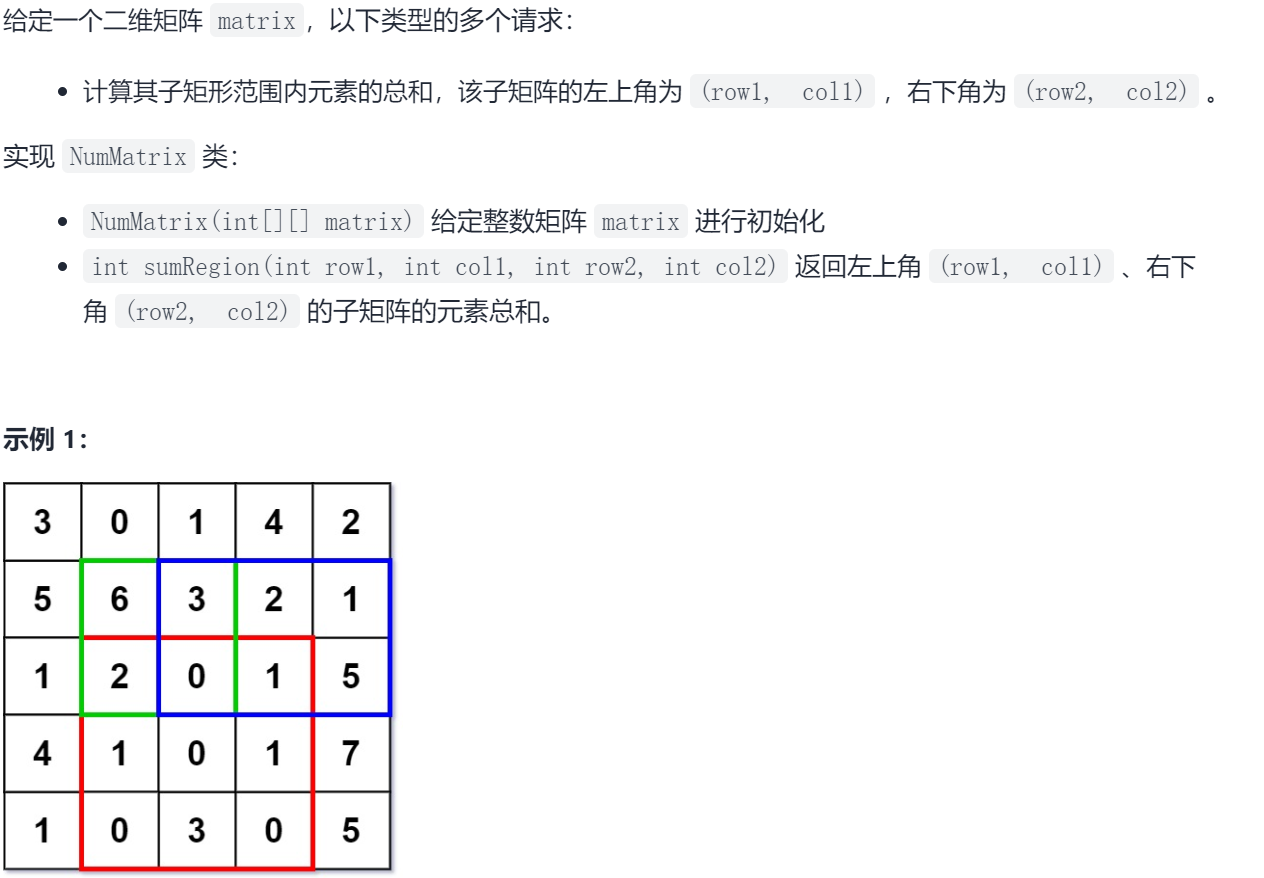
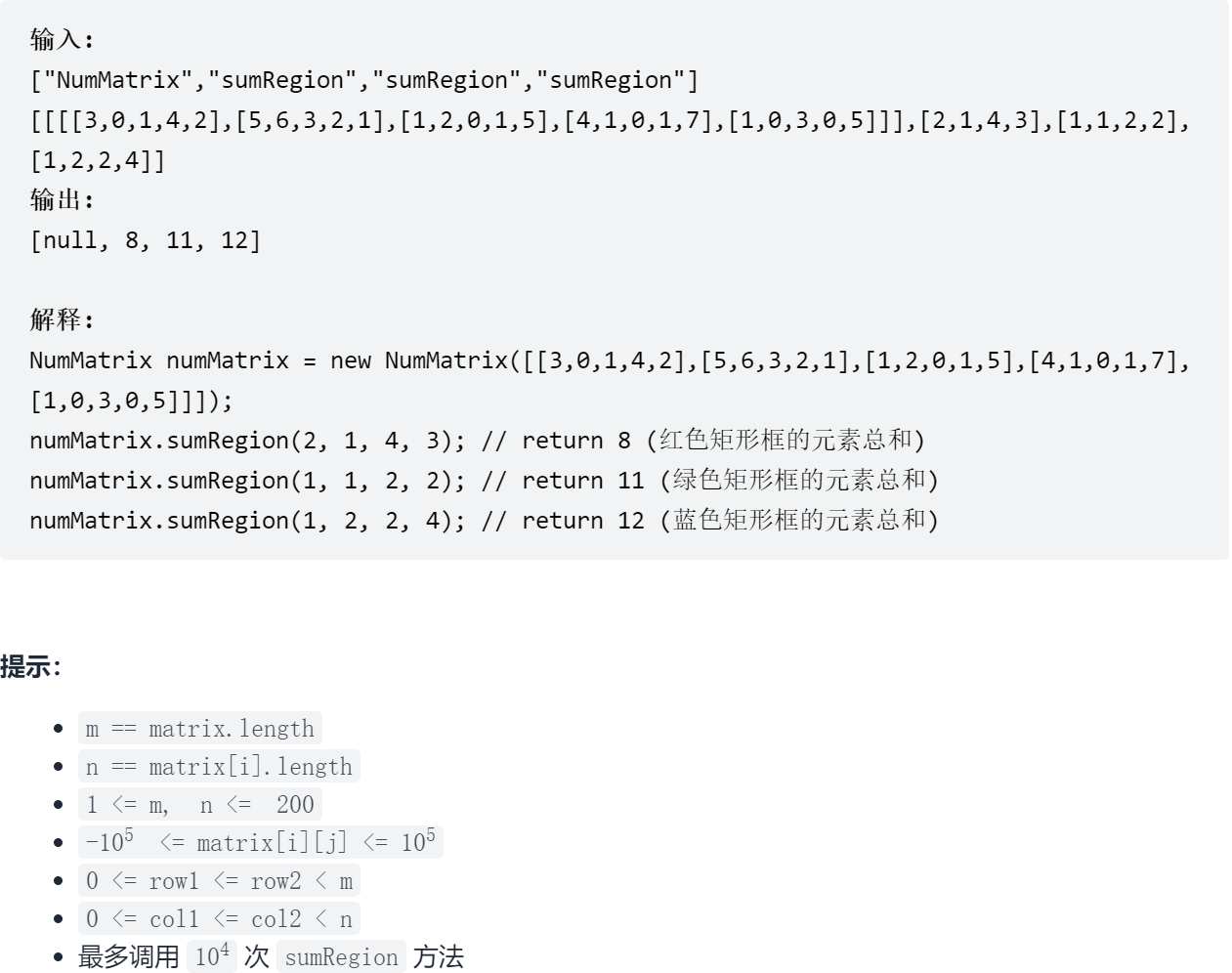
Sword finger Offer II 013 Sum of two-dimensional submatrix
13.1 problem solving
13.2 solution
Method 1: one dimensional prefix and
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
self.m, self.n = len(matrix), len(matrix[0])
# Calculate the prefix and of each row - the last column is used as the auxiliary column of column 0
self.prefix = [[0 for j in range(self.n+1)] for i in range(self.m)]
for i in range(self.m):
for j in range(self.n):
self.prefix[i][j] = self.prefix[i][j-1] + matrix[i][j]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
return sum(self.prefix[row][col2]-self.prefix[row][col1-1] for row in range(row1, row2+1))☆ method 2: two-dimensional prefix and ☆
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
m, n = len(matrix), (len(matrix[0]) if matrix else 0)
self.sums = [[0 for _ in range(n+1)] for _ in range(m+1)]
for i in range(m):
for j in range(n):
# Two plus one minus
self.sums[i+1][j+1] = self.sums[i][j+1] + self.sums[i+1][j] - self.sums[i][j] + matrix[i][j]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
# Two plus one minus
return self.sums[row2+1][col2+1] - self.sums[row1][col2+1] - self.sums[row2+1][col1] + self.sums[row1][col1]reference material:
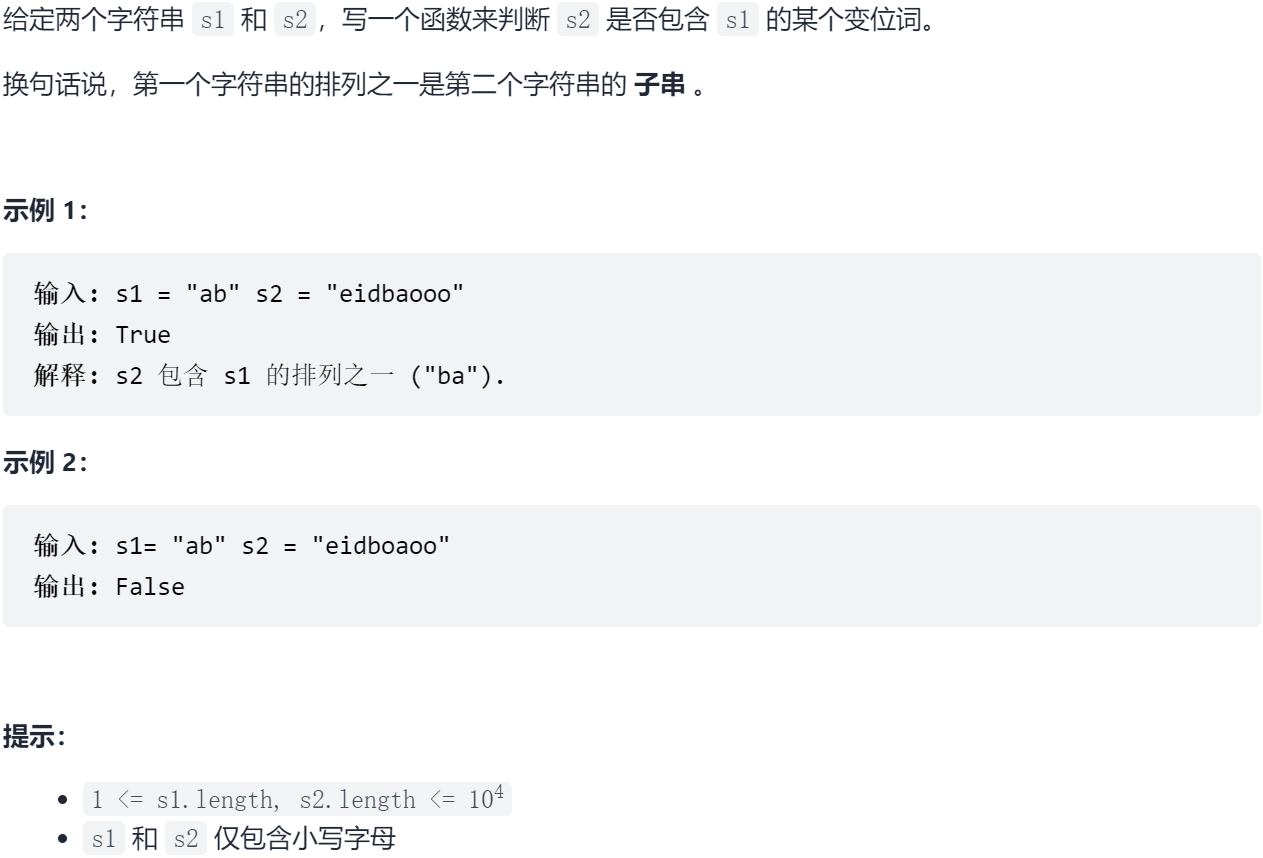
Sword finger Offer II 014 Anagrams in strings
14.1 problem solving
14.2 solution
Method 1: hash mapping sliding window
class Solution:
def checkInclusion(self, s1: str, s2: str) -> bool:
n1, n2 = len(s1), len(s2)
if n1 > n2:
return False
# Take the length of s1 as the initial value of the hash table sliding window key: val = alp: cnt
hashmap1, hashmap2 = collections.defaultdict(int), collections.defaultdict(int)
for i in range(n1):
# newly added
hashmap1[s1[i]] += 1
hashmap2[s2[i]] += 1
# compare
if hashmap1 == hashmap2:
return True
for j in range(n1, n2):
# Delete left window edge
hashmap2[s2[j-n1]] -= 1
if hashmap2[s2[j-n1]] == 0:
del hashmap2[s2[j-n1]]
# Add right window edge
hashmap2[s2[j]] += 1
# compare
if hashmap1 == hashmap2:
return True
return Falsereference material:
Sword finger Offer II 015 All modifiers in the string
15.1 problem solving

15.2 solution
Method 1: hash mapping sliding window
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
# String length
ns, np = len(s), len(p)
if ns < np:
return []
# Result index list
res = []
# Hash map sliding window
hashmaps, hashmapp = collections.defaultdict(int), collections.defaultdict(int)
for i in range(np):
# Add on the right side of the window
hashmaps[s[i]] += 1
hashmapp[p[i]] += 1
# judge
if hashmaps == hashmapp:
res.append(0) # Indexes
for j in range(np, ns):
# Delete on the left side of the window
hashmaps[s[j-np]] -= 1
if hashmaps[s[j-np]] == 0:
del hashmaps[s[j-np]]
# Add on the right side of the window
hashmaps[s[j]] += 1
# judge
if hashmaps == hashmapp:
res.append(j-np+1) # Indexes
return resreference material:
Sword finger Offer II 016
16.1 problem solving


16.2 solution
Method 1: double pointer + hash mapping
# 98.88% - 44ms
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
max_len = 0 # Maximum non repeating substring length
hashmap = {} # key: val = char: idx
lhs = -1 # The left pointer to the substring is not currently repeated
for rhs in range(len(s)):
cur = hashmap.get(s[rhs])
# Update lhs construct new left pointer position
if (cur is not None) and (cur > lhs):
lhs = cur
# The new index of new or updated s[rhs] is rhs
hashmap[s[rhs]] = rhs
# Update maximum length
max_len = max(max_len, rhs-lhs)
return max_len# 98.88% - 44ms - script 2
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
max_len = 0 # Maximum non repeating substring length
hashmap = {} # key: val = char: idx
lhs = -1 # The left pointer of the substring is not currently repeated
for rhs, char in enumerate(s):
if (char in hashmap) and (hashmap[char] > lhs):
# Update lhs construct new left pointer position
lhs = hashmap[char]
# Add or update the new index of char to rhs
hashmap[char] = rhs
else:
# The new index of new or updated s[rhs] is rhs
hashmap[char] = rhs
# Update maximum length
max_len = max(max_len, rhs-lhs)
return max_lenreference material:
Sword finger Offer II 017 Shortest string containing all characters ☆
17.1 problem solving


17.2 solution
Method 1: double pointer + hash sliding window
class Solution:
def minWindow(self, s: str, t: str) -> str:
# The length can never be satisfied
if len(s) < len(t):
return ""
left, right = 0, 0 # window left and right index
min_index = [0, len(s)] # Minimum length index
isFind = False # Have you ever found a string tag that meets the requirements
numValid = 0 # value key (alp) counter satisfied ☆
# Initialize requirements dictionary needs
needs = collections.Counter(t) # More convenient
# needs = {}
# for alp in t:
# if needs.get(alp) is None:
# needs[alp] = 0
# needs[alp] += 1
# Initialize the window (meet the requirements) dictionary window - only use the keys of needs to avoid recording other useless keys
window = {key: 0 for key in needs.keys()}
# iteration
while right < len(s):
new_alp = s[right] # Get new character
right += 1 # Move right border right
if window.get(new_alp) is not None: # window gets a
window[new_alp] += 1
if window[new_alp] == needs[new_alp]: # Satisfy a certain clause
numValid += 1
# Once the window covers all needs - the premise of moving the left boundary to the right ☆
while numValid == len(needs):
isFind = True # find
# Record the shortest length - both closed on the left and open on the right, so it is 1 less than the actual length
if right-left < min_index[1]-min_index[0]:
min_index = [left, right]
old_alp = s[left] # Remove old characters
left += 1 # Move left boundary right
# Keys not from needs do not affect or operate
if window.get(old_alp) is not None: # window remove a
window[old_alp] = max(window[old_alp]-1, 0) # At least 0
if window[old_alp] < needs[old_alp]: # Do not meet a certain requirement
numValid -= 1
# s(left: right)
return s[min_index[0]: min_index[1]] if isFind else ""reference material:
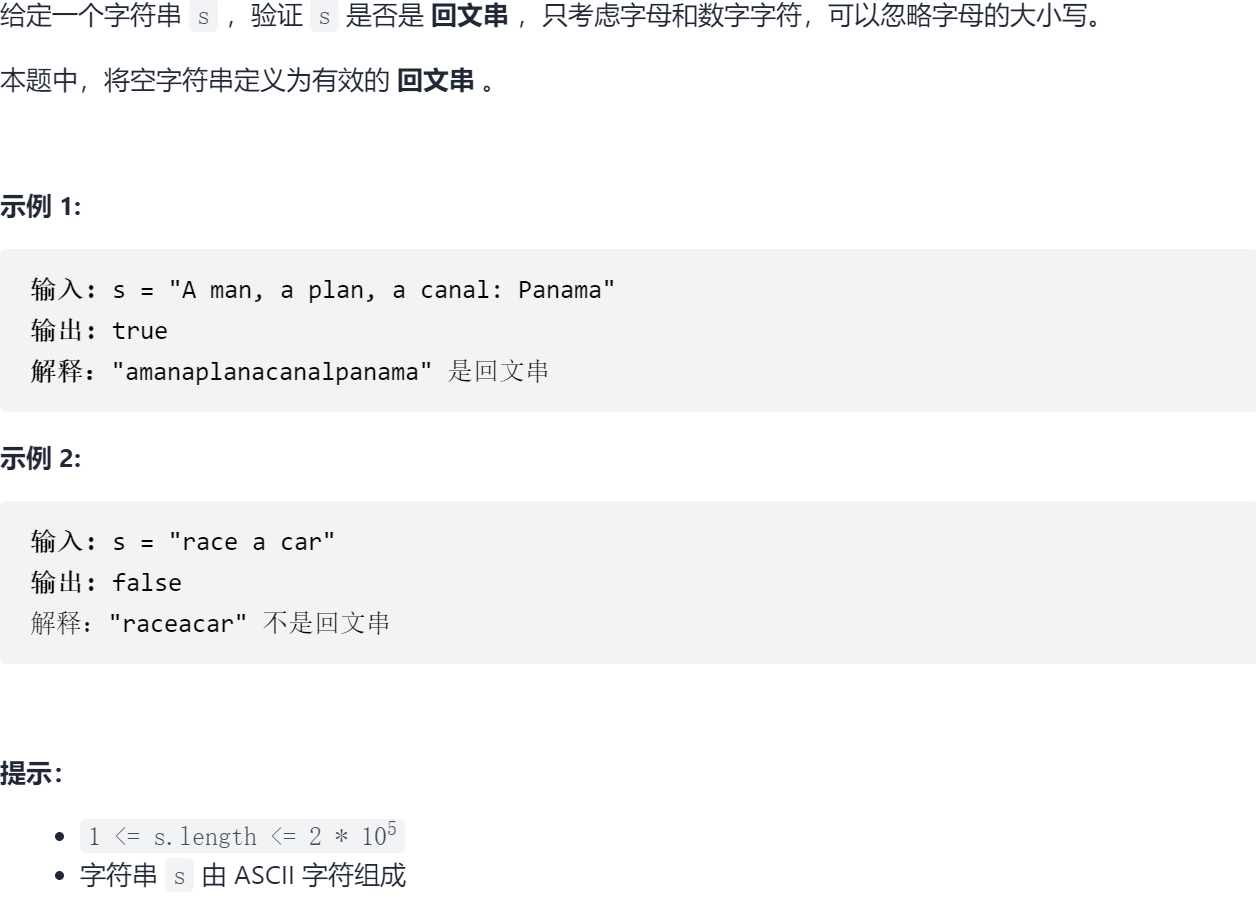
Sword finger Offer II 018 Valid palindrome
18.1 problem solving
18.2 solution
Method 1: cleaning + traversal
# 98.90% - 32ms
class Solution:
def isPalindrome(self, s: str) -> bool:
# 1. Data cleaning
tmp = [c.lower() for c in s if c.isalnum()] # isalnum is equivalent to isalpha or isdigit
# 2. Traversal comparison
n = len(tmp)
for i in range(n // 2):
if tmp[i] != tmp[n-1-i]:
return False
return Truereference material:
Sword finger Offer II 019 Delete at most one character to get a palindrome
19.1 problem solving
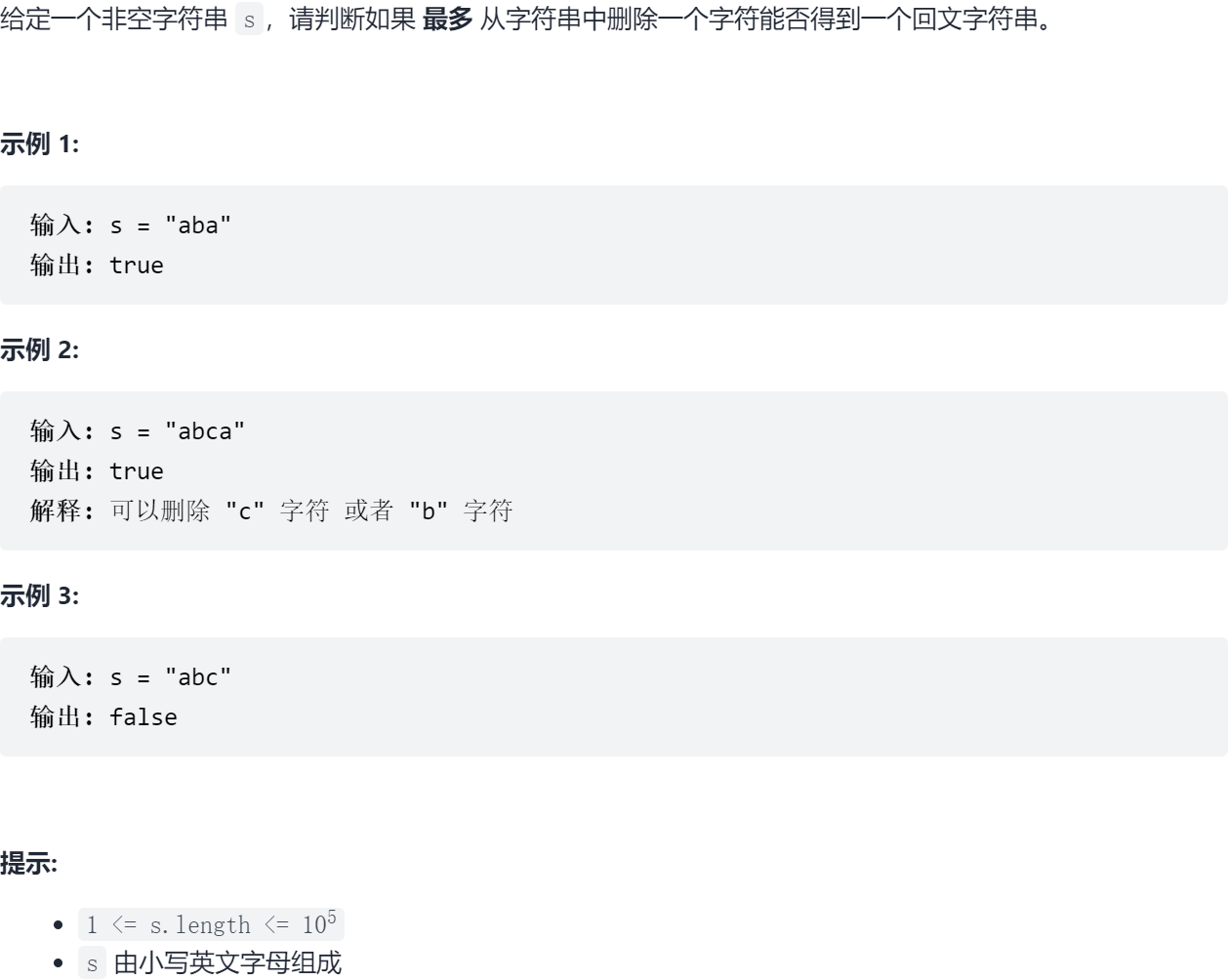
19.2 solution
Method 1: delete the matching of characters on the left and right respectively
# 80.81% - 124ms
class Solution:
def validPalindrome(self, s: str) -> bool:
def match(lhs, rhs):
# Traverse the matching from both ends to the center one by one
while lhs < rhs and s[lhs] == s[rhs]:
lhs += 1
rhs -= 1
return lhs, rhs
# Normal matching
lhs, rhs = match(0, len(s)-1)
if lhs >= rhs:
return True
# Delete the currently mismatched left character
lhs1, rhs1 = match(lhs+1, rhs)
if lhs1 >= rhs1:
return True
# Delete the currently mismatched right character
lhs2, rhs2 = match(lhs, rhs-1)
if lhs2 >= rhs2:
return True
# Still do not match
return Falsereference material:
Sword finger Offer II 020 Number of palindrome substrings ☆
20.1 problem solving
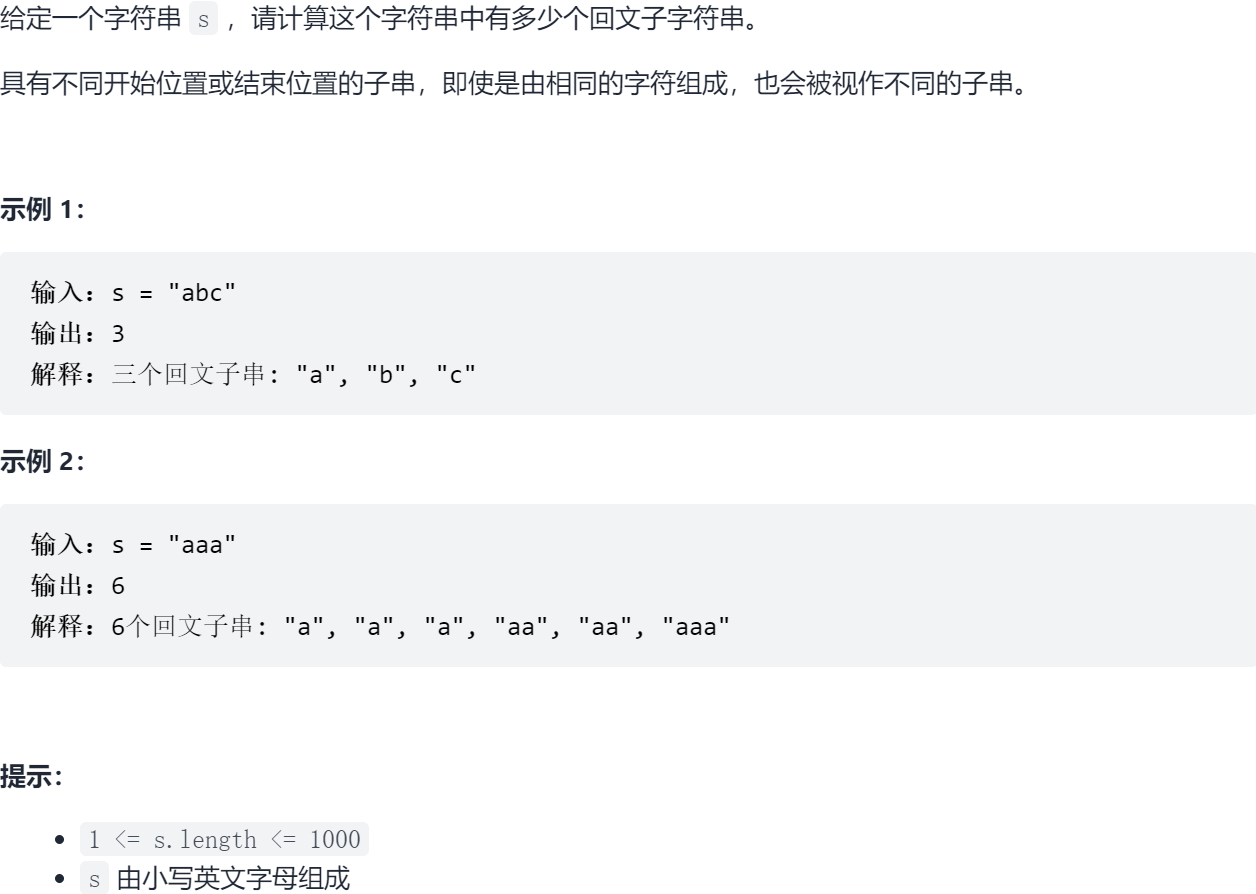
20.2 solution
Method 1: dynamic programming
# 50% - 196ms
class Solution:
def countSubstrings(self, s: str) -> int:
res = 0
n = len(s)
# dp[i][j] indicates whether s[i, j] is a palindrome string
dp = [[False for _ in range(n)] for _ in range(n)]
for i in range(n-1, -1, -1):
for j in range(i, n):
# state transition
if s[i] == s[j] and (j - i < 2 or dp[i+1][j-1] is True):
dp[i][j] = True
res += 1
return resMethod 2: Manacher algorithm (horse drawn cart)
# 99.46% - 40ms
class Solution:
def countSubstrings(self, s: str) -> int:
# Horse drawn cart algorithm (Manacher)
# https://leetcode-cn.com/problems/a7VOhD/solution/hui-wen-zi-zi-fu-chuan-de-ge-shu-by-leet-ejfv/
# Insert between all adjacent characters # (placeholders at the beginning and end) to ensure that all palindrome strings found are of odd length
t = ["$", "#"]
for c in s:
t.append(c)
t.append("#")
n = len(t)
t.append("!")
# f[i] represents the maximum palindrome radius of extension Exhibition with the ith bit of t as the palindrome center
f = [1 for _ in range(n)]
imax = rmax = res = 0
# Enumerate each position i of t and first assume that i is the palindrome center
# If f[i] is known, the right endpoint rmax of I is i + f[i] - 1
for i in range(1, n): # Note that i starts from 1
# Initialize f[i]
# If i < = Rmax, it indicates that the current i is included in the current maximum palindrome substring
# Suppose J is the symmetric position of I about the palindrome center IMAX of this maximum palindrome (i.e. j+i = 2) × imax)
# f[i] is at least equal to min{f[j], rmax − i+1} = min(f[2*imax-i], rmax-i+1)
# If f[i] and rmax − i+1 are taken as small, it is necessary to ensure that the palindrome string is within the current maximum palindrome string
if i <= rmax:
f[i] = min(rmax-i+1, f[2*imax-i])
# Center expansion
while t[i+f[i]] == t[i-f[i]]:
f[i] += 1
# Maintain imax and rmax dynamically
if i + f[i] - 1 > rmax:
imax = i # i with the largest rmax is imax
rmax = i + f[i] - 1 # Update larger rmax
# Statistical answer, the current contribution is rounded up to (f[i] - 1) / 2
res += (f[i] // 2)
return resreference material:
Sword finger Offer II 021 Delete the penultimate node of the linked list
21.1 problem solving
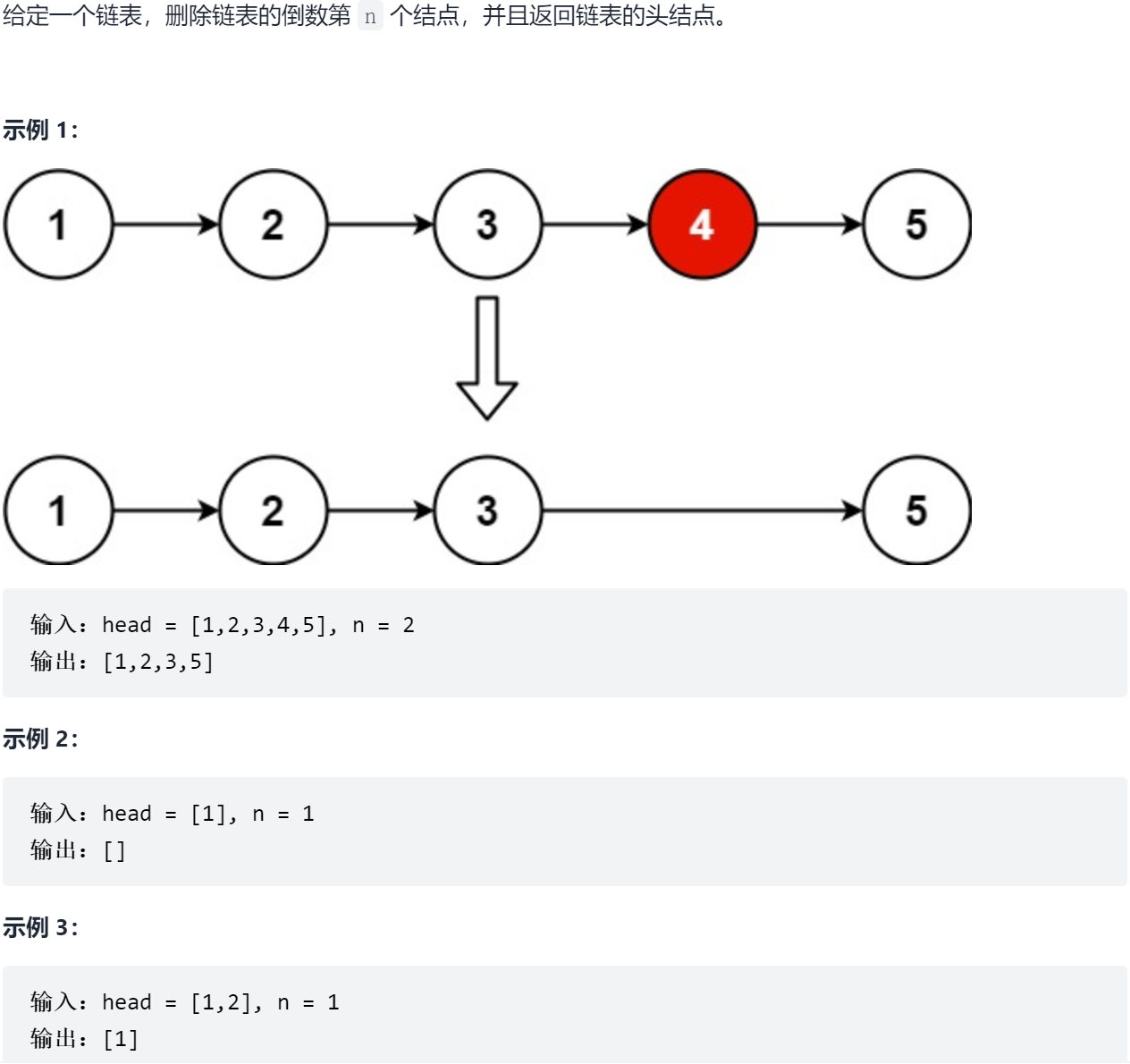

21.2 solution
Method 1: speed pointer
# 98.84% - 24ms
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
# Pseudo head - sentinel node - easy to delete head node
dummy = ListNode(-1)
dummy.next = head
lhs = rhs = head # Speed pointer
lcnt = rcnt = 1 # Speed counter
while rhs.next:
# Slow pointer
lhs = lhs.next
lcnt += 1
# Quick pointer
rhs = rhs.next
rcnt += 1
if rhs.next:
rhs = rhs.next
rcnt += 1
# Length of the second half
diff = rcnt - lcnt
# Starting from the midpoint (second half)
if n <= diff:
tmp = lhs
step = diff - n
# Starting from the starting point (first half)
else:
tmp = dummy
step = rcnt - n
# Move and jump delete
for _ in range(step):
tmp = tmp.next
tmp.next = tmp.next.next if tmp.next else None
return dummy.nextreference material:
Sword finger Offer II 022 The entry node of the link in the linked list ☆
22.1 problem solving

22.2 solution
Method 1: speed pointer
# 70.79% - 48ms
class Solution(object):
def getIntersect(self, head):
slow = head # Slow pointer slow = tortoise
fast = head # fast pointer = Rabbit hare
while fast and fast.next:
slow = slow.next # One step at a time
fast = fast.next.next # Take two steps at a time
if slow == fast: # If there is a first encounter node, it is proved that there is a ring
return slow
return None
def detectCycle(self, head):
# Empty linked list
if not head:
return None
# Acyclic linked list
intersect = self.getIntersect(head)
if not intersect:
return None
# To find the entrance to the cycle, we have two pointers traverse at the same speed
# one from the front of the list, and the other from the point of intersection.
ptr1 = head # Starting from the starting point of the linked list
ptr2 = intersect # Starting from the meeting node ☆
while ptr1 != ptr2: # The second encounter node is the ring entry node
ptr1 = ptr1.next # One step at a time
ptr2 = ptr2.next # One step at a time
return ptr1reference material:
Sword finger Offer II 023 The first coincident node of two linked lists
23.1 problem solving
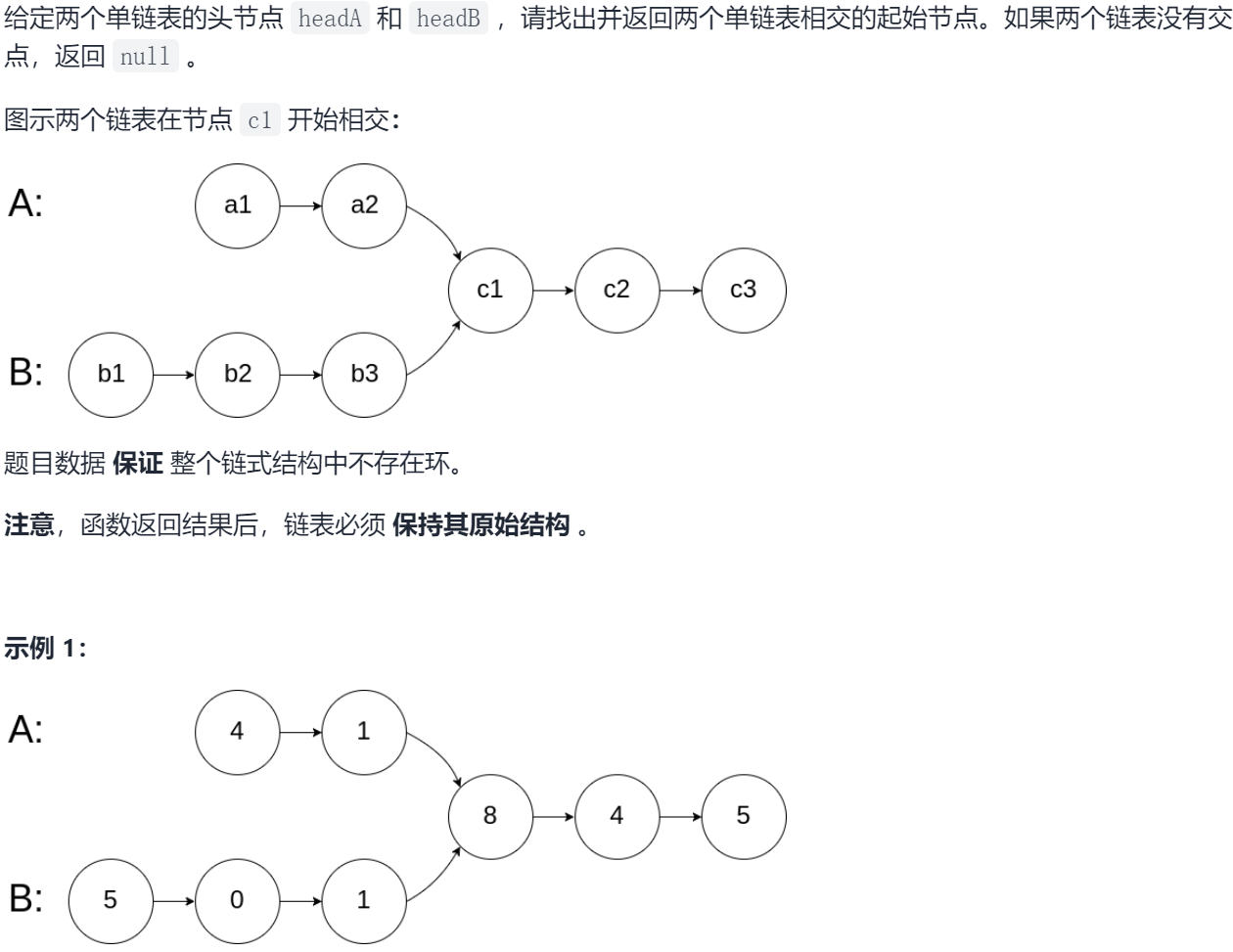
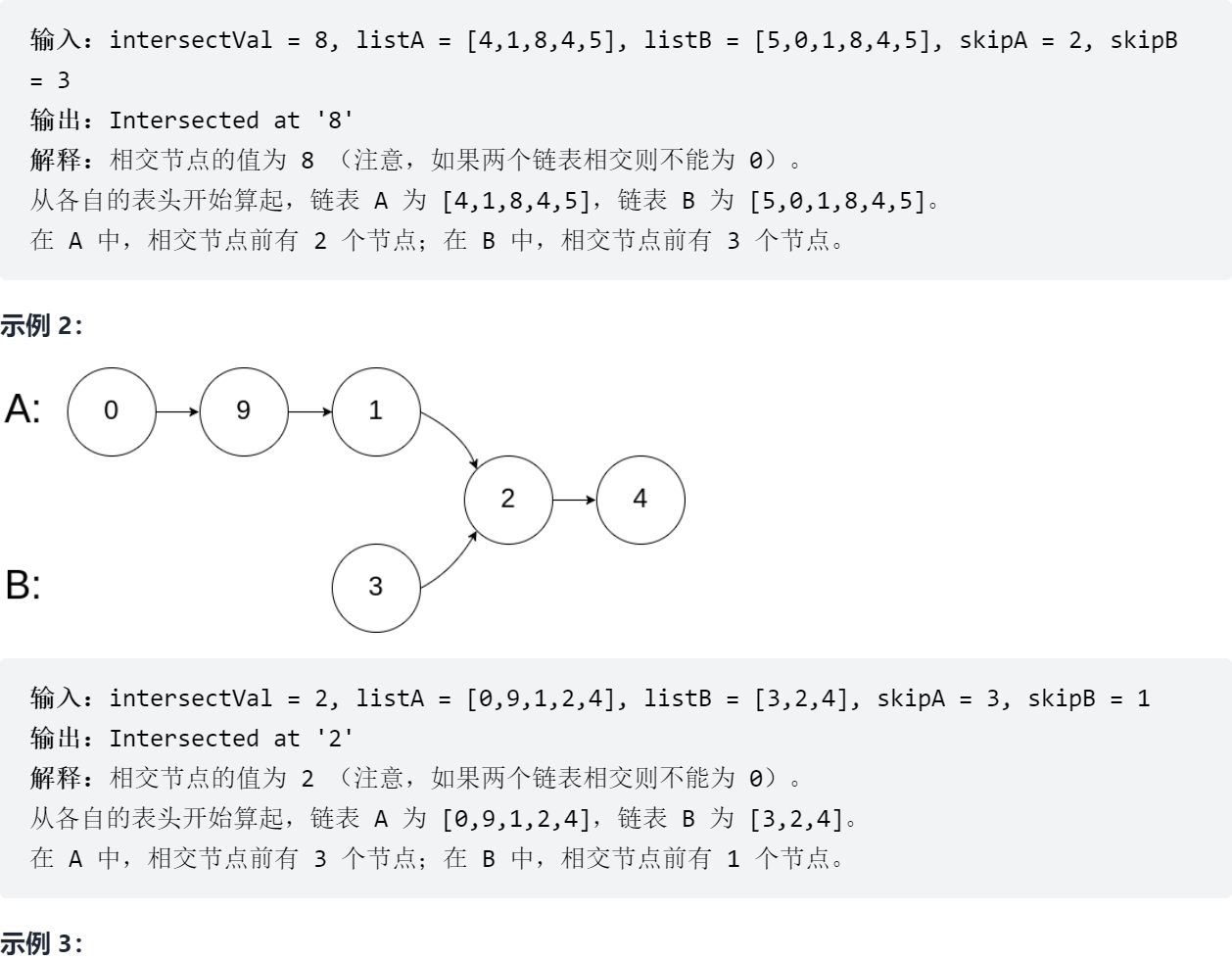

23.2 solution
Method 1: double pointer
# 94.62% - 124ms
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
ptrA, ptrB = headA, headB
# If and only if ptrA and ptrB are None at the same time, there is no coincidence
# The following order is immutable!!
while ptrA or ptrB:
# 1. Starting point of first exchange
if ptrA is None:
ptrA = headB
elif ptrB is None:
ptrB = headA
# 2. Judge coincidence node
if ptrA is ptrB:
return ptrA
# 3. Take a step
ptrA = ptrA.next
ptrB = ptrB.next
return Nonereference material:
Sword finger Offer II 024
24.1 problem solving
24.2 solution
Method I:
reference material: