First, let's look back:
The code is as follows:
class Solution {
public:
vector<string> permutation(string s) {
vector<string> ans;
string str;
sort(s.begin(),s.end());
vector<int> visit(s.size(),0);
permutationCore(ans,str,s,0,visit);
return ans;
}
void permutationCore(vector<string>& ans,string &str,string &s,int k,vector<int> &visit)
{
if(k==s.size())
{
ans.push_back(str);
return;
}
for(int i=0;i<s.size();++i)
{
if(visit[i] || (i>0&&!visit[i-1]&&s[i-1]==s[i])) continue;
visit[i]=1;
str+=s[i];
permutationCore(ans,str,s,k+1,visit);
// str-=s[i];
str.pop_back();
visit[i]=0;
}
}
};Although it is violence, I still encounter many problems:
1.string is overloaded with - =, but pop similar to vector can be used_ Back implementation
2. The repetition of characters was not considered when writing for the first time...
Then see the official problem solution, which is solved in this way. First sort the characters in the string, and then let each recursive layer select the leftmost free character of the repeated sequence of letters to be selected. emmm good sub, good method! The time complexity should be O(n^2), and the space complexity is a little unknown......
result:
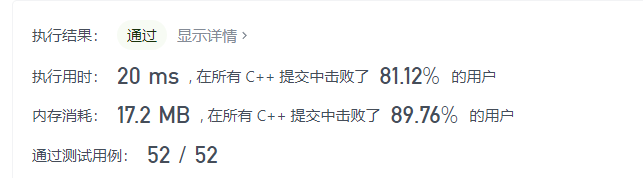
Then I looked at the sword finger offer. There is a full arrangement of exchange, which is also very powerful
The idea is like this:
For the first character of each string, exchange and all subsequent characters, and then fully arrange the subsequent strings
The code is as follows:
class Solution {
public:
vector<string> permutation(string s) {
vector<string> ans;
permutationCore(ans,s,0);
return ans;
}
void permutationCore(vector<string>& ans,string &s,int k)
{
if(k==s.size())
{
for(int i=0;i<ans.size();++i)
{
if(ans[i]==s)
return;
}
ans.push_back(s);
return;
}
for(int i=k;i<s.size();++i)
{
swap(s[k],s[i]);
permutationCore(ans,s,k+1);
swap(s[k],s[i]);
}
}
};Of course, this is beyond the time limit...
Because in order to detect whether there is the same string in ans.push_ A loop detection is added before back......
However, if you really want to use this method, you can replace the vector of the answer with a set. Hey, the code is as follows:
class Solution {
public:
vector<string> permutation(string s) {
unordered_set<string> ans;
permutationCore(ans,s,0);
return vector<string>(ans.begin(),ans.end());
}
void permutationCore(unordered_set<string>& ans,string &s,int k)
{
if(k==s.size())
{
ans.insert(s);
return;
}
for(int i=k;i<s.size();++i)
{
swap(s[k],s[i]);
permutationCore(ans,s,k+1);
swap(s[k],s[i]);
}
}
};
Tell me the details of the second method:
1. Make a strong turn when you return
2. Interface of insert
Ah, then there is the second answer to the official question. The idea is probably as follows:
Get a string that is a little larger than the original string from bottom to top. HMM, it's almost the same
Direct CV:
class Solution {
public:
bool nextPermutation(string& s) {
int i = s.size() - 2;
while (i >= 0 && s[i] >= s[i + 1]) {
i--;
}
if (i < 0) {
return false;
}
int j = s.size() - 1;
while (j >= 0 && s[i] >= s[j]) {
j--;
}
swap(s[i], s[j]);
reverse(s.begin() + i + 1, s.end());
return true;
}
vector<string> permutation(string s) {
vector<string> ret;
sort(s.begin(), s.end());
do {
ret.push_back(s);
} while (nextPermutation(s));
return ret;
}
};
Can only say that the official answer is cow!! But what does reverse mean...
Then follow the official link to see the full array of things:
Now my understanding of reverse is that it assumes that the current string is two parts, one is a sequence increasing from right to left (which can be understood as ASCII), and then there is another part on the left, and the rightmost number on the left is smaller than the leftmost number of the right sequence.
For example, 12354, the increasing sequence from right to left is 54 on the right. Then what we want to think about is how to find the next arrangement that is just a little larger (i.e. adjacent) than it? If we solve it directly by hand, we should think like this, right: 54 is so big, which is already the maximum value that can be composed of two digits in it. Then exchange a maximum number in the left part with a number just as big as him in the right sequence, so that 3 becomes 4, that is, the hundred bits are only 1. Is it just a little larger?
The result is to replace it with 12453. If you find it, the original sequence is increasing from right to left. In fact, after the exchange, it must have the same property, that is, the original sequence is still increasing from right to left, but if we want the smallest, we have to change 53 into 12435. Ah, it's like this is the number we want, isn't it.
Of course, the above example has a little particularity, that is, 54 has the largest two digits that can be composed in it. In fact, as long as the right meets the increasing sequence from right to left, do you have some questions? I have two:
1. What if there is only one number in the right part (the penultimate number is smaller than the penultimate number)? If there is only one number, it can be regarded as a right part.
2. If the right part is not the largest, such as 1247653, it is the same. It becomes 1257643 first and then 1253467. emmm feels that it doesn't quite understand what it says, but the core idea is one: find the next arrangement that is a little larger than the current arrangement (listen to your words as listen to your words)......
The algorithm steps are as follows (regardless of the sequence on the right, the next adjacent arrangement larger than the current arrangement is obtained):
Direct cv:
Algorithm process
The standard "next permutation" algorithm can be described as:
Find the first adjacent ascending element pair (i,j) from back to front, which satisfies a [i] < a [J]. At this point [j,end) must be in descending order
Find the first k satisfying A[i] < A[k] from back to front in [J, end]. A[i] and A[k] are respectively the "decimal" and "large" mentioned above
Exchange A[i] with A[k]
It can be concluded that [j,end) must be in descending order and [J, end] must be reversed to make it in ascending order
If no matching adjacent element pair can be found in step 1, it indicates that the current [begin,end) is in a descending order, then skip to step 4 directly
This method supports data duplication and is adopted in C++ STL.
Author: imageslr
Link: https://leetcode-cn.com/problems/next-permutation/solution/xia-yi-ge-pai-lie-suan-fa-xiang-jie-si-lu-tui-dao-/
Source: LeetCode
The copyright belongs to the author. For commercial reprint, please contact the author for authorization, and for non-commercial reprint, please indicate the source.