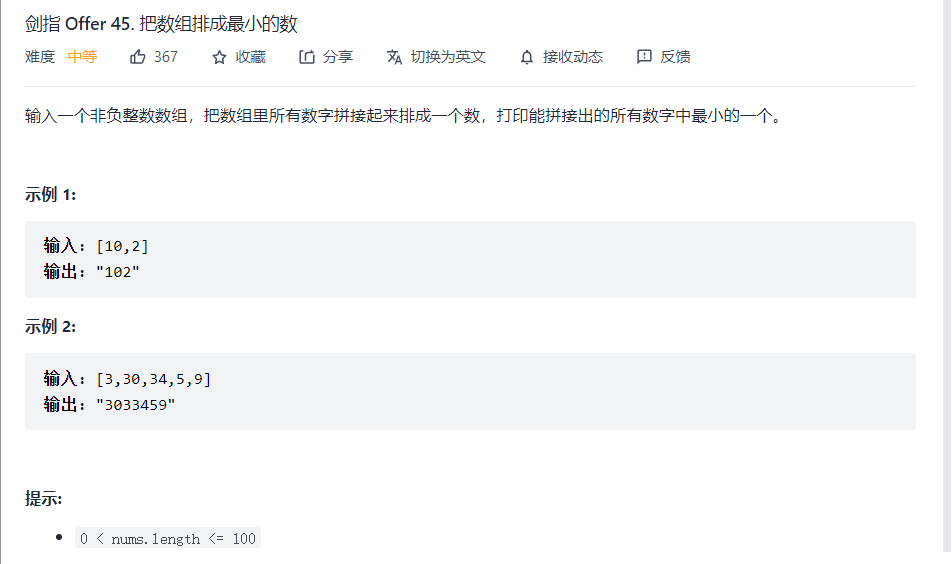
A string or says it's a math problem

1. Violence

Ah, at first glance, we will think that if we find out the full arrangement of strings and then sort to select the smallest, but this is O(n!) Time complexity, I'm afraid this has to explode

2. Mathematical proof + sorting

First of all, both the book and the solution give a definition, that is, two integers m and N. if Mn > nm is spliced, M > N, NM > Mn is n > m, and equality is the same. Then the official website directly arranges an order. Some small partners may not understand why they are the smallest according to the nature of this size.

Here cv "sword finger offer" proves that:

With these three properties, does it feel like something in discrete mathematics or linear algebra is proving?

We can assume that our sorted string is x1x2 X... Y... Xn, if this is not the minimum, then suppose that the exchange X and y have x1x2 Y... X... Xn<X1X2...X...Y...Xn, then we just need to explain x1x2 Y... X... Xn>X1X2...X...Y...Xn can introduce contradiction.

The condition we know is x1x2 X... Y... Xn is sorted out. According to the definition, there is x < y. suppose there is an m in front of Y, then M < y is YM > My. Does this mean x1x2 X... MY... Xn<X1X2... X... YM... Xn, that is, wait until y is switched forward until it is switched near the position of X, the whole string will become larger and larger, and the same is true for the backward switching of small X, so x1x2 Y... X... Xn>X1X2...X...Y...Xn is established, and it is concluded that the minimum splicing is actually a sorting problem from small to large according to the size relationship defined above.

The official hand rolled out a quick code, which can be used for reference:

class Solution {
public:
    string minNumber(vector<int>& nums) {
        vector<string> strs;
        for(auto i=nums.begin();i!=nums.end();++i)
        {
            strs.push_back(to_string(*i));
        }
        // for(int i = 0; i < nums.size(); i++)
        //     strs.push_back(to_string(nums[i]));
        quickSort(strs,0,strs.size()-1);
        string ans;
        for(string &s:strs)
            ans.append(s);
            // ans.push_back(s);
        return ans;
    }

    void quickSort(vector<string>& strs,int l,int r)
    {
        if(l>=r) return;
        int i=l,j=r;
        while(i<j)
        {
            while(strs[j]+strs[l]>=strs[l]+strs[j]&&i<j) j--;//Add an equal sign here and always pay attention to I < J
            while(strs[i]+strs[l]<=strs[l]+strs[i]&&i<j) i++;
            swap(strs[i],strs[j]);
        }
        swap(strs[i],strs[l]);
        quickSort(strs,l,i-1);
        quickSort(strs,i+1,r);
    }
};

Here are some details:

1.to_string(int) can convert an integer into a string and return it. Accumulate it

2. Pay attention to the writing method of fast row, take the leftmost element as the middle rotating axis, and always pay attention to the conditions of the cycle. Such a cycle ensures that I < = J when it comes out, so there must be STRs [l] > = STRs [i], so it is feasible to exchange out of the cycle

3. Don't write the recursive interval wrong

The results are as follows:

Then turn down the problem solution. Ah, there is also a library adjustment thing, of course. After all, it can improve the efficiency of our code writing. No, continue cv hey hey:

class Solution {
public:
    string minNumber(vector<int>& nums) {
        vector<string> strs;
        string res;
        for(int i = 0; i < nums.size(); i++)
            strs.push_back(to_string(nums[i]));
        sort(strs.begin(), strs.end(), [](string& x, string& y){ return x + y < y + x; });
        for(int i = 0; i < strs.size(); i++)
            res.append(strs[i]);
        return res;
    }
};

Author: jyd
 Link: https://leetcode-cn.com/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof/solution/mian-shi-ti-45-ba-shu-zu-pai-cheng-zui-xiao-de-s-4/
Source: force buckle( LeetCode)
The copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.

The results are as follows:

Is the C + + library too strong? Sometimes the score of this force buckle is a little confused Don't you understand?