0. Title Description

1. Sword finger Offer II 001 Integer division
2. Title Description: divide integers and round the result (discard decimal places)
3. Title Requirements: do not use *, /,%
4. Constraint condition: [- 231 - 1]. If the division result overflows, 231 - 1 will be returned

1. Content description

1. The following four solutions come from Easy to understand Java/C++ /Python/js/go - integer division (Sword finger)
2. Before looking at the solution, when I tried the idea of bit operation, I didn't know how to deal with the shift divisor 2. Later, after looking at the solution to understand the idea, I had a deep understanding of the boundary problem

2. Solution 1: subtraction instead of division

Version ①: A and b are positive, cycle condition b ≤ a, exceeding the time limit

class Solution {
    public int divide(int a, int b) {
        if(a == Integer.MIN_VALUE && b == -1){
            return Integer.MAX_VALUE;
        }
        boolean sign = (a > 0) ^ (b > 0) ? true : false;
        a = a > 0 ? a : -a;
        b = b > 0 ? b : -b;
        int cnt = 0, temp = b;
        while(b <= a){
            b += temp;
            cnt++;
        }
        return sign ? -cnt : cnt;
    }
}

Version ②: A and b are negative, the cycle condition a ≤ b, and the operation passes

class Solution {
    public int divide(int a, int b) {
        if(a == Integer.MIN_VALUE && b == -1){
            return Integer.MAX_VALUE;
        }
        boolean sign = (a > 0) ^ (b > 0) ? true : false;
        a = a > 0 ? -a : a;
        b = b > 0 ? -b : b;
        int cnt = 0;
        while(a <= b){
            a -= b;
            cnt++;
        }
        return sign ? -cnt : cnt;
    }
}

The analysis of the two items is planned to be understood from the bytecode level and written down for the time being
The core idea of the above code:

1. The symbol bits are extracted separately, and the symbols are added after the results are calculated by the same sign of a and B
   Skills worthy of reference: use ternary operators to obtain the results of a and B symbolic operations
   boolean sign = (a > 0) ^ (b > 0) ? true : false;， Boolean is used here instead of int, because the former is one byte and the latter is two bytes. Whether they will affect efficiency has not been studied

2. Overflow processing: consider the data range [- 231 - 1], 231 needs to be considered here
   a == Integer.MIN_VALUE && b == -1

3. Analysis on -231 the relationship between the two: java int type overflow?

3. Solution 2: subtraction optimization to reduce time complexity

Core idea: subtract the multiple of divisor every time you try

code:

class Solution {
    public int divide(int a, int b) {
        if(a == Integer.MIN_VALUE && b == -1){
            return Integer.MAX_VALUE;
        }
        boolean sign = (a > 0) ^ (b > 0) ? true : false;
        a = a > 0 ? -a : a;
        b = b > 0 ? -b : b;
        int cnt = 0;
        while(a <= b){
            int t = b;
            int k = 1;
            while(t > 0xc0000000 && a < t + t){
                t += t;
                k += k;
            }
            a -= t;
            cnt += k;
        }
        return sign ? -cnt : cnt;
    }
}

Description of T > = 0xc00000000 & & A < = t + T

1. None of the above codes take =, the test is passed, and both sides take ==
2. Explanation of 0xc00000000
   
3. Explanation of a < = t + T when t == 0xc00000000:
   ① t + t = -215
   ② Value range of a [- 215 - 1]
   ③ When a = -215, a == t + t is satisfied

4. Solution: three bit operation optimization, time complexity reduced to O(1)

Core idea: in 3 It is realized by bit operation
code:

class Solution {
    public int divide(int a, int b) {
        if(a == Integer.MIN_VALUE && b == -1){
            return Integer.MAX_VALUE;
        }
        boolean sign = (a > 0) ^ (b > 0) ? true : false;
        a = Math.abs(a);
        b = Math.abs(b);
        int cnt = 0;
        for(int i = 31; i >= 0; i--){
            if((a >>> i) - b >=0){
                a -= b << i;
                cnt += 1 << i;
            }
        }
        return sign ? -cnt : cnt;
    }
}

Code analysis:

1. Priority: > > > >+=
2. (a > > > I) - explanation of b > = 0 instead of (a > > > I) > = b
   ① About math abs(Integer.MIN_VALUE) == Integer. MIN_ VALUE

/**
     * <p>Note that if the argument is equal to the value of
     * {@link Integer#MIN_VALUE}, the most negative representable
     * {@code int} value, the result is that same value, which is
     * negative.
     * @return  the absolute value of the argument.
     */
    public static int abs(int a) {
        return (a < 0) ? -a : a;
    }

Note: if the input parameter in the comment is integer MIN_ Value, integer MIN_ VALUE
That is, math The result of ABS () is negative

② Verification of (a > > > I) positivity and negativity

public static void main(String[] args) {
        System.out.println(test.count);
        int a = -3;
        int b = Integer.MIN_VALUE;
        //int b = Integer.MAX_VALUE;
        System.out.println(a + b);
        System.out.println(Math.abs(b));
        for(int i = 31; i >= 0; i--){
            System.out.println("b "+ b + " >>> i" + i + " ---- " + (b >>> i));
        }
    }

Test b: take the maximum and minimum values respectively

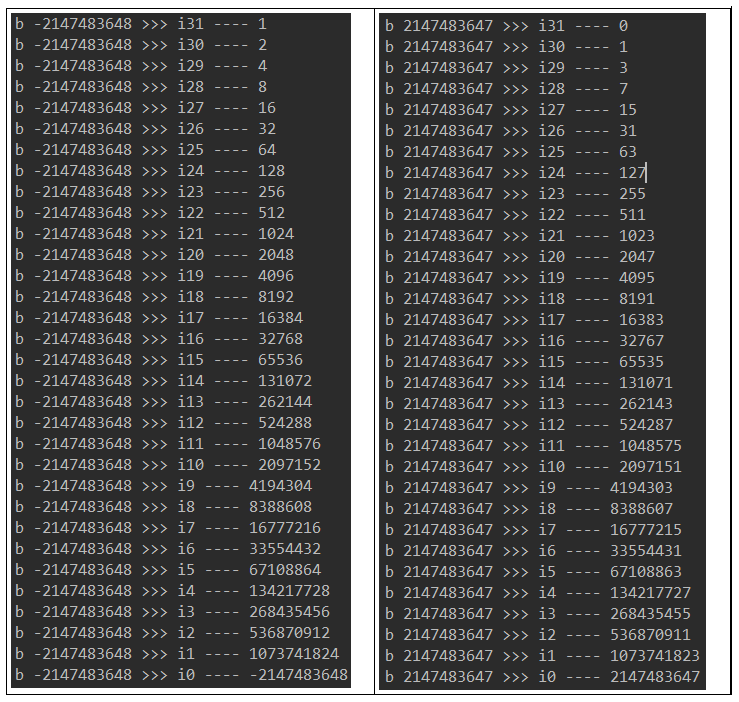
Test results:
① When B = integer MIN_ Value (a > > > I) > = B is always true and enters the dead cycle
② When B = integer MIN_ Value is converted as follows

Let m = (a > > > I)
Then M - b > = 0 is equivalent to - (B - M) > = 0
The range of M > 0, - (B - M) is - [0, integer. Max_value] < 0. The equation does not hold