Tree article

Question 1: depth of binary tree

Enter a binary tree and find the depth of the tree. The nodes (including root and leaf nodes) passing from root node to leaf node form a path of the tree. The length of the longest path is the depth of the tree, and the depth of the root node is regarded as 1.

Data range: the number of nodes meets 0 ≤ n ≤ 100, and the value on the node meets 0 ≤ val ≤ 100
Advanced: space complexity O(1), time complexity O(n)

If the input use case is {1,2,3,4,5, #, 6, #, #, 7}, the figure below shows:

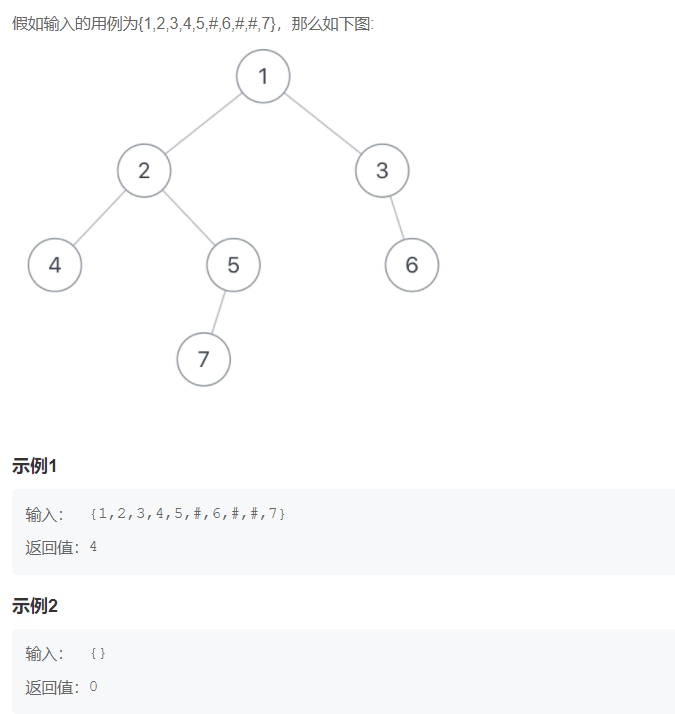
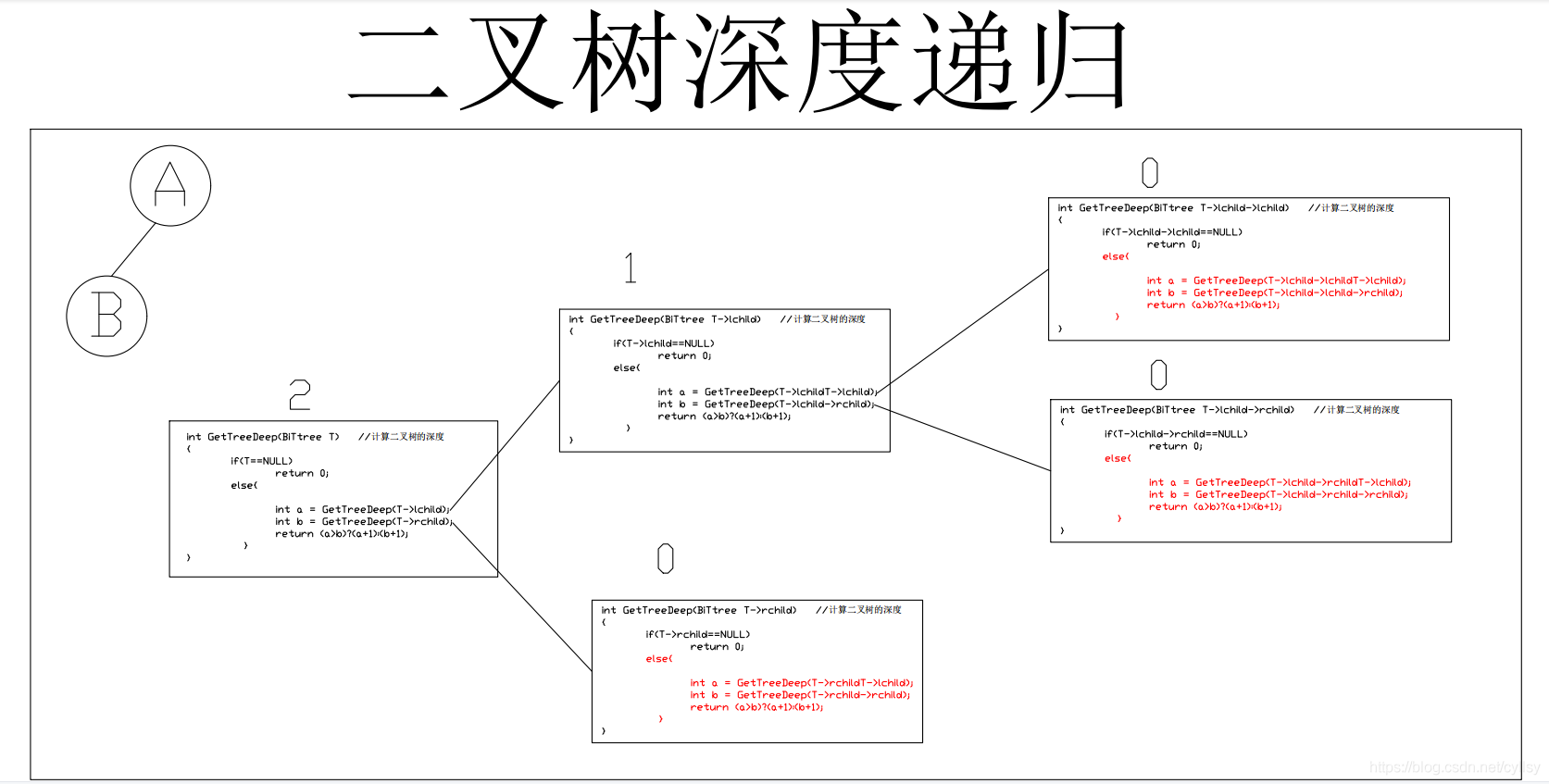
Topic idea: when a node is passed in and this method is called, the depth of the tree with the incoming node as the root node should be returned, and the depth of the tree must be related to the depth of the left and right subtrees, so after entering this method, It includes the depth of the left and right subtrees (and to get the depth of the left and right subtrees, it must be obtained by calling the method again with the left and right child nodes as the root nodes, so recursion is carried out at this time), and there is a process of comparing the left and right depths, and then take the larger value, which is the value with the deeper depth of the left and right subtrees of the node, and take the value + 1 as the return value, Is the depth of the node.

See the following figure:

Code part:

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    int TreeDepth(TreeNode* pRoot) {
    if (pRoot==NULL){
        return 0;
    }
        else{
        //Declare a and b variables to record the obtained left and right subtree depths respectively.
            int a=TreeDepth(pRoot->left);
            int b=TreeDepth(pRoot->right);
            //For comparison, the larger value + 1 is used as the return value
            return a>b?(a+1):(b+1);
        }
    }
};

Question 2: image of binary tree

describe
Operate the given binary tree and transform it into a mirror of the source binary tree.
Data range: the number of nodes of the binary tree is 0 ≤ n ≤ 1000, and the value of each node of the binary tree is 0 ≤ val ≤ 1000
Requirement: space complexity O(n). This problem also has in-situ operation, that is, the solution of spatial complexity O(1) and time complexity O(n)

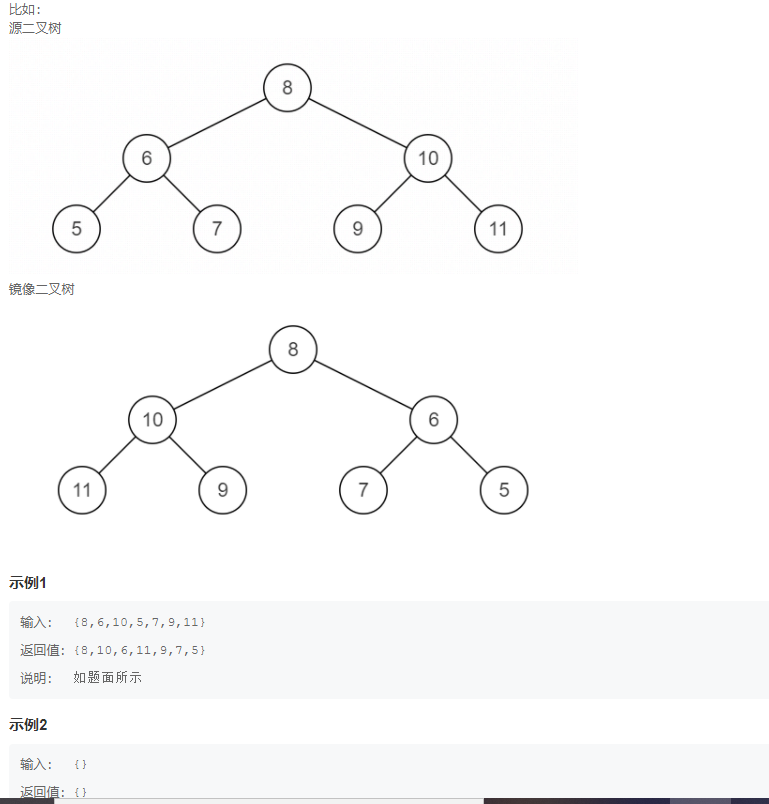
Topic idea: as shown in the figure below, what we need to do is to change the order of the left and right subtrees of each layer from top to bottom. So far, the recursive method can be adopted.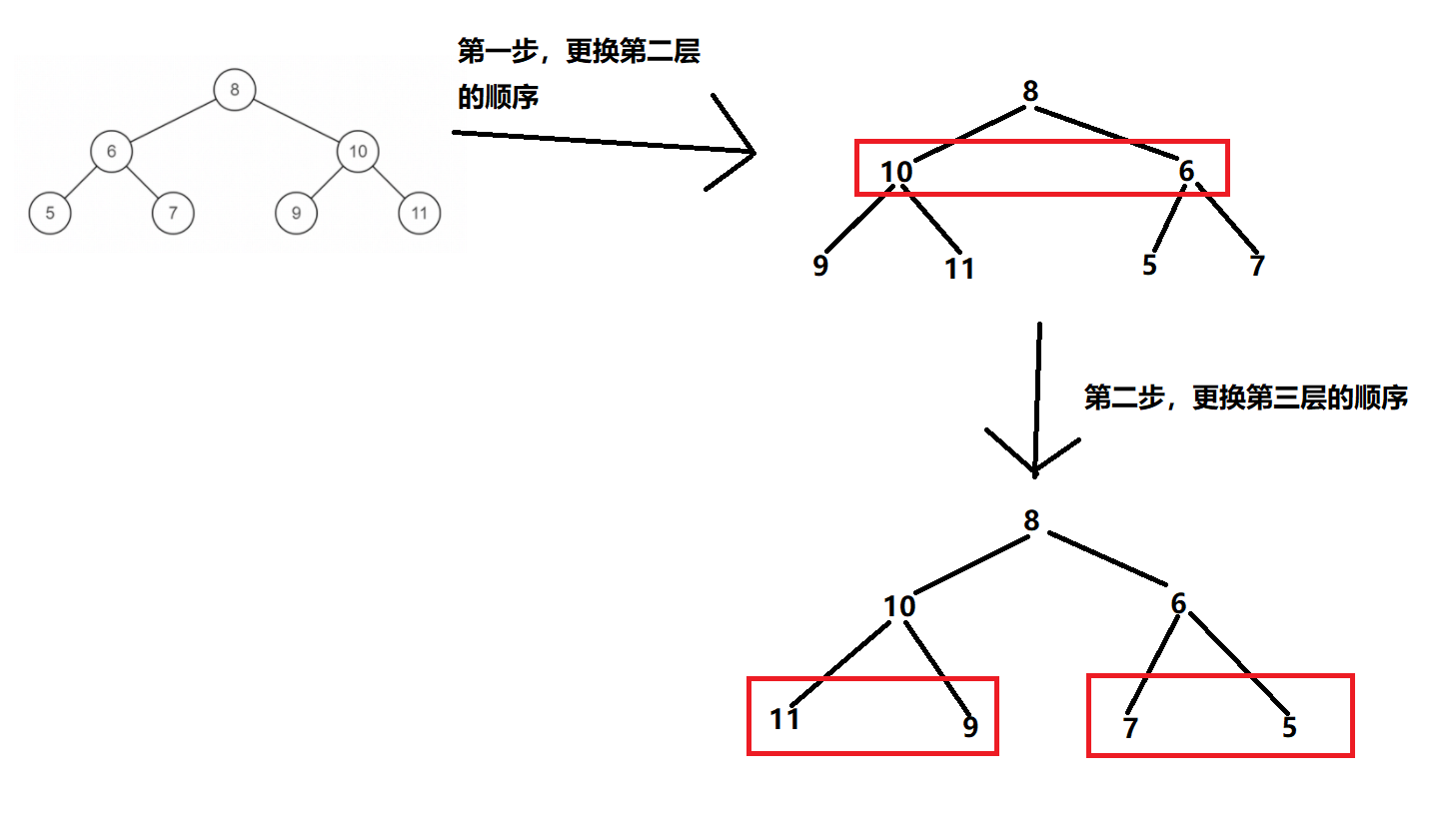

Code part:

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
public:
    /**
     * The class name, method name and parameter name in the code have been specified. Do not modify them. Just return the value specified by the method directly
     *
     * 
     * @param pRoot TreeNode class 
     * @return TreeNode class
     */
    TreeNode* Mirror(TreeNode* pRoot) {
        if(pRoot==NULL){
            return pRoot;
        }
        //Exchange information of left and right subtrees
        TreeNode* temp=pRoot->left;
        pRoot->left=pRoot->right;
        pRoot->right=temp;
        //Then continue to exchange the subtrees of the left and right subtrees, and directly recurse here
        Mirror(pRoot->left);
        Mirror(pRoot->right);
        //Finally, the information of the root node is returned
        return pRoot;
    }
};

Question 3: print binary tree from top to bottom

describe
Each node of the binary tree is printed from top to bottom without branches, and the nodes of the same layer are printed from left to right. For example, enter {8,6,10, #, #, 2,1}, as shown in the example binary tree in the following figure, then print 8,6,10,2,1 in turn (empty nodes are not printed, skip). Please store the printed results in an array and return.
Data range:
0 < = total number of nodes < = 1000
-1000 < = node value < = 1000

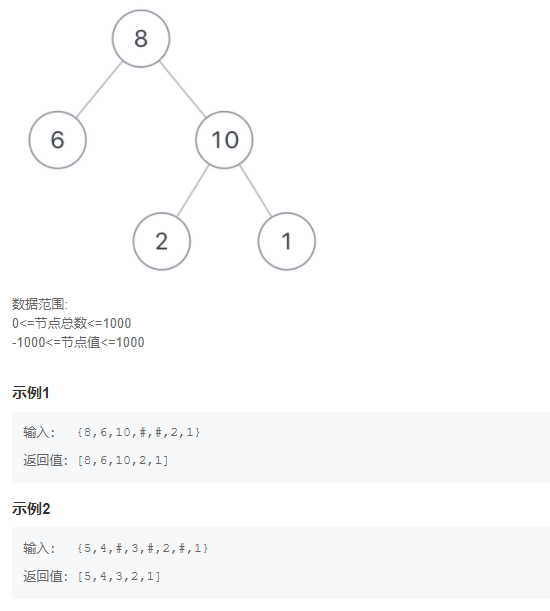
Topic idea:
The topic gives a binary tree. We need to traverse the nodes from top to bottom and from left to right. That is, the traversal from top to bottom.
For BFS (breadth first algorithm), we can use a queue to store the nodes we need to access. When we visit a node, we put the value of the node into the array to be output, and then the node goes out of the queue. Then we first judge whether the node on the left is empty. If it is not empty, the node pointer will be queued, and the judgment of the node on the right is the same. It continues until the queue is empty. In addition, remember that the special judgment root node is empty
Supplement!
Breadth first search (BFS) is a search algorithm based on queue. In short, its search process is similar to "throwing a stone into the lake and causing layers of ripples".

Depth first search (DFS) is a recursive search algorithm. In short, the search process is similar to "don't hit the south wall and don't look back".

BFS focuses on queues, while DFS focuses on recursion. This is their essential difference.

Code part:
You can also further understand the whole search process in combination with drawing

class Solution {
public:
    vector<int> PrintFromTopToBottom(TreeNode* root) {
        vector<int> ret;  //An array of results
        if (!root) return ret;
        queue<TreeNode*> q;  //Define a queue
        q.push(root);        //Transfer root node into queue
        while (!q.empty()) {
            TreeNode *node = q.front();  //Assign the value of the root node to * node
            ret.push_back(node->val);
            q.pop();  //Pop up root node
            
            if (node->left) q.push(node->left);  //If the left subtree is not empty, join the left subtree in the queue
            if (node->right) q.push(node->right);//If the right subtree is not empty, the right subtree will be queued
        }
        return ret;
    }
};

Question 4: symmetric binary tree

describe
Given a binary tree, judge whether it is its own mirror image (i.e. whether it is symmetrical)
For example, the following binary tree is symmetrical

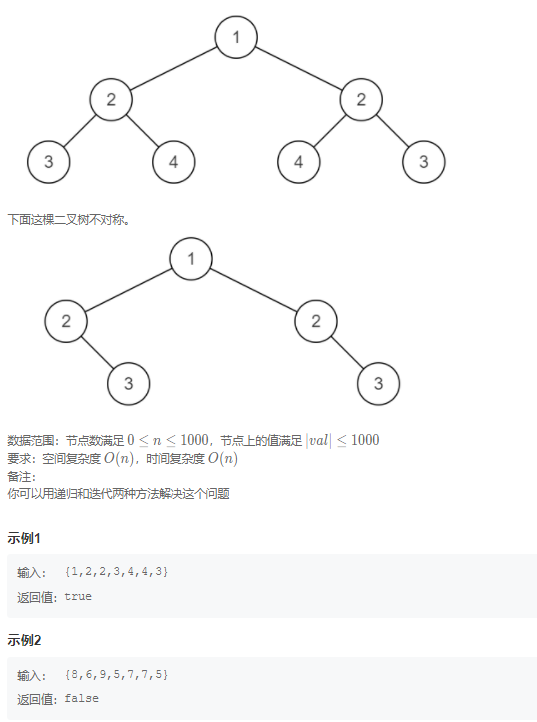
Topic idea:
The "symmetry" requirement is met if and only if two subtrees meet the following requirements:

• The root node values of the two sub trees are the same;

The left and right subtrees of the two subtrees are symmetrical respectively, including:

• The values of the corresponding positions of the left subtree of a tree and the right subtree of b tree are equal
• The values of the corresponding positions of the right subtree of a tree and the left subtree of b tree are equal

Specifically, we can design a recursive function check to pass in the head nodes a and b of the two subtrees to be tested (for this problem, we can pass in root). In a single query, there is an obvious Base Case to judge whether the subtree is "symmetrical":

• a and b are empty nodes: meet the requirements of "symmetry";
• One of the nodes a and b is empty, which does not meet the "symmetry" requirement;
• The values of a and b are not equal and do not meet the requirements of "symmetry";

In other cases, we should check whether the left and right nodes of a and B are "symmetrical", that is, recursively call check(a.left, b.right) and check(a.right, b.left).

Code part:

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot) {
    return check(pRoot,pRoot);//Enter the check function to check from the root node
    }
    bool check(TreeNode* a,TreeNode* b){  //One left and one right
        if((a==NULL)&&(b==NULL))return true;   //If both are empty, they are mirrored
        if((a==NULL)||(b==NULL))return false;  //One is empty and the other is not empty. It is not a mirror image
        if((a->val)!=(b->val))return false;  //The two values are not equal and are not mirrored
        return check(a->left,b->right)&&check(a->right,b->left);  //Continue to recursively check the left and right subtrees
    }
};

Question 5: paths with a certain value in a binary tree (1)

describe
Given a binary tree root and a value sum, judge whether there is a path where the sum of node values from the root node to the leaf node is equal to sum.
1. The problem path is defined as the node from the root node of the tree to the leaf node
2. Leaf nodes refer to nodes without child nodes
3. The path can only be from parent node to child node, not from child node to parent node
4. The total number of nodes is n
Topic idea:

Define recursive function function: judge whether the sum of the path from the current node to root is sum

• Each recursion subtracts the value of the passing node
• The current node is a leaf node, and sum is just 0, indicating that the path sum is just sum
• When returning, ensure that each node can be recursive, and only one path is required to meet it

Illustration: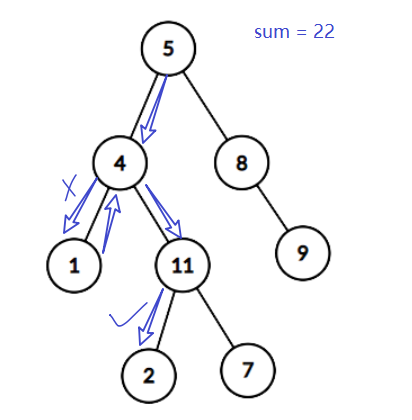

Code part:

/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param root TreeNode class 
     * @param sum int integer 
     * @return bool Boolean
     */
    bool hasPathSum(TreeNode* root, int sum) {
      if (root == NULL)
            return false;
        // Each recursion subtracts the value of the passing node
        sum -= root->val;
        // The current node is a leaf node, and sum is just 0, indicating that the path sum is just sum
        if (sum == 0 && root->left == NULL && root->right == NULL)
            return true;
        // Ensure that each node can be recursive, and only one path is required to meet it
        // In essence, DFS depth first traversal is only implemented recursively
        return hasPathSum(root->left, sum) || hasPathSum(root->right, sum);
    }
};

Question 6: judge whether it is a balanced binary tree

describe
Enter a binary tree with n nodes to judge whether the binary tree is a balanced binary tree.
Here, we only need to consider its balance, not whether it is a sorted binary tree
Balanced Binary Tree has the following properties: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1 (that is, it is OK to be equal to 1), and both the left and right subtrees are a Balanced Binary Tree.
Example explanation: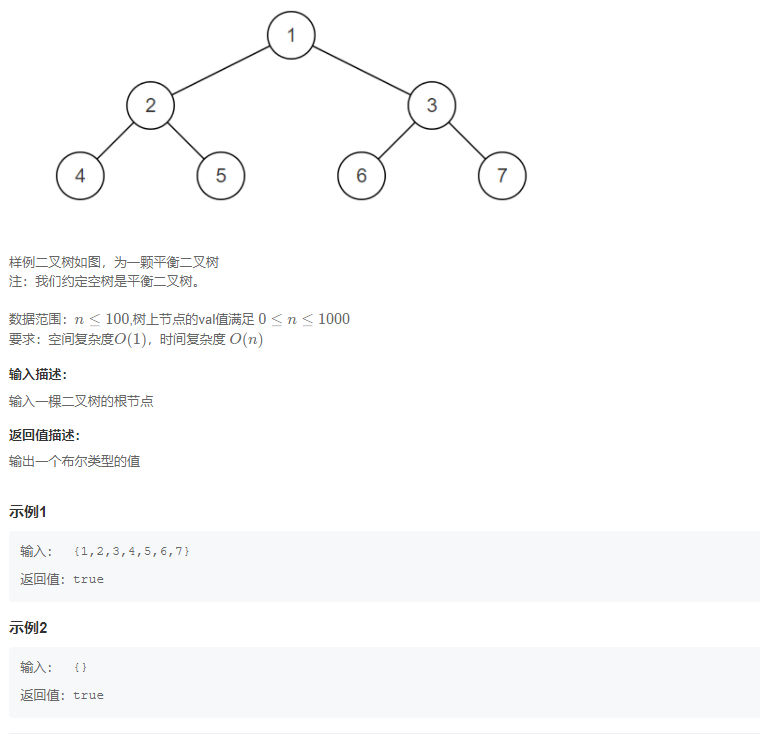
Topic idea:
Solution 1: top down (pre order traversal)
The condition for a binary tree to be a "balanced binary tree" is that the tree is empty, or the height difference between its left and right subtrees is up to 1. Therefore, to judge whether a binary tree is balanced, we need to calculate the height of its subtree and compare the height difference between the left and right subtrees.

Therefore, the steps to solve this problem are as follows:

• The function getHeight(root) of "find the height of binary tree" is designed to find the height of binary tree with root as the root node;
• Traverse the original binary tree and call getHeight(root) function for each node. If the height difference between the left and right subtrees is greater than or equal to 2, it is unbalanced; Otherwise, it is a balanced binary tree.
  The idea of finding the height of binary tree is shown in the figure.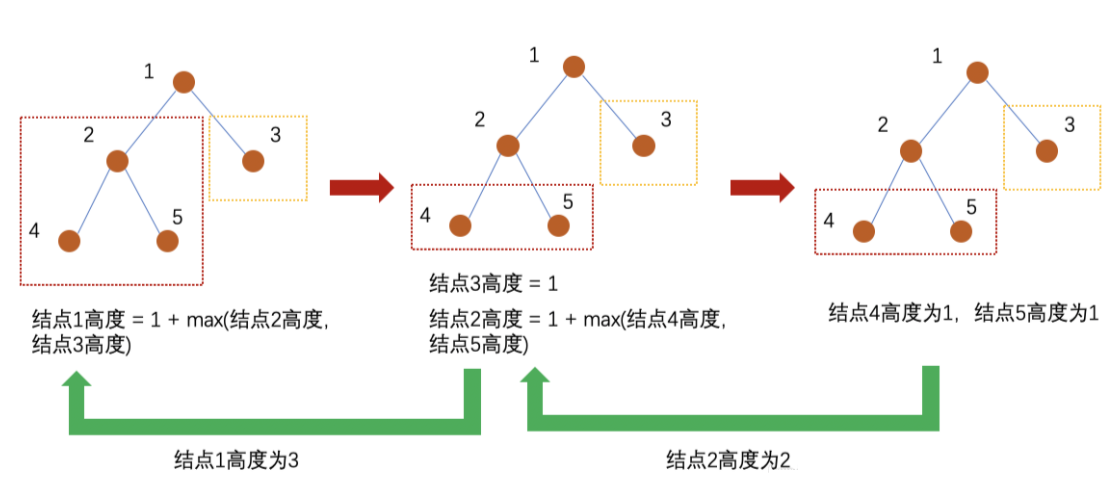

In the figure, the direction of the red arrow is the recursive direction, and the direction of the green arrow is the backtracking direction.

• When the node is empty, its height is 0;
• When the node has no left child or right child, its height is 1;
• Otherwise, the height of the node is max (left subtree height, right subtree height) + 1. (add 1 because you want to add the node itself)

Code part:

class Solution {
public:
    bool IsBalanced_Solution(TreeNode* root) {
        if (!root)  //If it is empty, it is a balanced binary tree
            return true;
        // Calculate the height of the left subtree and the right subtree respectively
        int leftHeight = getHeight(root->left), rightHeight = getHeight(root->right);
        // If the height difference of subtree is greater than 1, false is returned
        if (abs(leftHeight - rightHeight) > 1) 
            return false;
        // Recursively judge whether the left and right subtrees are balanced
        return IsBalanced_Solution(root->left) && IsBalanced_Solution(root->right);
    }
    // Function for finding subtree height
    int getHeight(TreeNode* root) {
        if (!root) 
            return 0;
        if (!root->left && !root->right) 
            return 1; // leaf node 
        return 1 + max(getHeight(root->left), getHeight(root->right));
    }
};

Solution 2: bottom-up (post order traversal)
Solution 1 traverses the nodes of the tree when "calculating the height of the binary tree" and traverses the nodes of the tree again when "judging whether it is balanced", so repeated calculation occurs.
Specifically, when judging from 1, you should traverse 2, 4 and 5 when calculating the depth with the getHeight function, and 4 and 5 when judging whether the tree with 2 as the root is a balanced binary tree. Therefore, there are many repeated calculations in this method.
The optimization of solution 1 adopts the "bottom-up" problem-solving idea:

• Starting from the lowest leaf node, calculate the height of the node. If the node is unbalanced, return - 1 directly, and do not continue to calculate the height of other nodes, otherwise return its height;
• If the bottom-up process is always balanced, the final tree is balanced. In this method, each node (in the worst case) will be traversed only once, and there will be no double calculation.

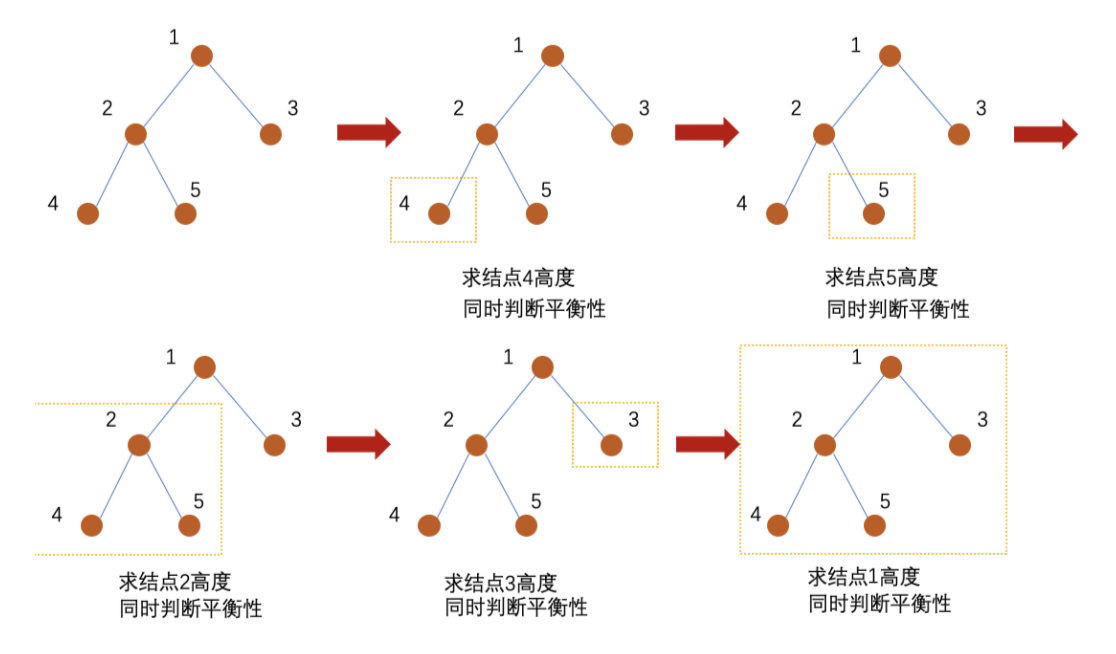
Code part:

class Solution {
public:
    bool IsBalanced_Solution(TreeNode* pRoot) {
        if (!pRoot) 
            return true; 
        return getHeight(pRoot) >= 0; // If the result is not - 1, it is balanced
    }
    int getHeight(TreeNode* root) {
        if (!root) 
            return 0;   //The subtree is empty when recursing to the leaf node, which is used for backtracking
        // Left subtree height
        int left = getHeight(root->left); 
        if (left == -1) 
            return -1; // If the height of the left subtree is - 1, it is unbalanced
        int right = getHeight(root->right); // Right subtree height
        if (right == -1 || abs(left - right) >= 2) 
            return -1; // If the height of the right subtree is - 1, or the difference between the height of the left and right subtrees is greater than 1, it is unbalanced
        return 1 + max(left, right); // Returns the height of the node
    }
};