T2 dynamic programming & & decision monotonicity optimization
Pre cheese: Mo team
General meaning:
Given an interval with n numbers, it is exactly divided into k segments to minimize the logarithm of the same number in each segment of the interval.
Data range:
1<=n<=100000,1<=k<=min(n,20),1<=ai<=n.
Example:
10 2
1 2 1 2 1 2 1 2 1 2
8
Idea:
Let dp[i][j] represent the minimum value of the first I number divided into j segments. Enumerate the breakpoint K, where dp[i][j]=min{dp[k][j-1]+sum(k+1,i)}. In fact, this k is monotonic, which can be optimized by classical 1D dynamic programming.
Almost everyone can think of this interval DP, and how to judge the monotonicity of k and 1D dynamic programming optimization is the difficulty.
Monotonicity judgment of k:
If sum(i,j) satisfies the quadrilateral inequality, then dp [] has decision monotonicity.
What is emmm quadrilateral inequality?
For any integer a,b,c,d on the definition field, where a ≤ b ≤ C ≤ D, sum(a,d)+sum(b,c) ≥ sum(a,c)+sum(b,d) holds, then the function w satisfies the quadrilateral inequality
(another definition)
For any integer a,b on the definition field, where a < B
If sum (a, B + 1) + sum (a + 1, b) ≥ sum (a, b) + sum (a + 1, B + 1) holds, then the function w satisfies the quadrilateral inequality.
At the same time, for the above two definitions, if the equal sign is constant, it satisfies the quadrilateral identity
As for proof... Please read oi wiki by yourself.
So how to prove that sum () in this problem satisfies the quadrilateral inequality?
This needs to be proved by mathematical induction, but I won't prove it. In fact, I can't, or I can't use the method of table observation.
Then we can start after proving the quadrilateral inequality
Decision monotonicity Optimization:
Nature: if f[i] satisfies the monotonicity of decision, for any decision point g[i], there is always a decision point g[i + 1] > = g[i] (or < = g[i]) of f[i+1]
prove:

Here, we can only get the lower bound of each enumeration l according to the monotonicity of decision, but we can't determine its upper bound. Therefore, simply implementing the state transition equation still can not optimize the worst-case time complexity.
However, this problem conforms to a simple case, that is, the value of the transfer function has been completely determined before dynamic programming. The state transition equation is as follows:
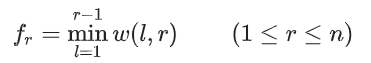
In this case, we define the process DP (l,r,kl,kr) to represent the state value of solving fl~fr, and know that the optimal decision point of these States must be located in [kl,kr], and then use the divide and conquer algorithm as follows:
void DP(int l, int r, int k_l, int k_r)
{
int mid = (l + r) / 2, k = k_l;
// Finding the optimal decision point of state f[mid]
for (int i = k_l; i <= min(k_r, mid - 1); ++i)
if (w(i, mid) < w(k, mid)) k = i;
f[mid] = w(k, mid);
// According to the monotonicity of decision, the decision interval of the left and right parts is obtained and processed recursively
if (l < mid) DP(l, mid - 1, k_l, k);
if (r > mid) DP(mid + 1, r, k, k_r);
}
In this way, the time complexity is optimized to be very excellent when served with the pre cheese mozzarella team
O(k* n* log(n)^2)!
But because I can't do all the above things in the exam, I can only write a 30 point violence range dpQAQ
30 point code:
#include<bits/stdc++.h>
using namespace std;
int n,k,f[5000][5000],a[100005],dis[5000][5000];
int solve(int x,int y)
{
int b[100005],tmp=0;
memset(b,0,sizeof(b));
for(int i=x;i<=y;i++)
{
b[a[i]]++;
}
for(int i=1;i<=100000;i++)
{
if(b[i]) tmp+=(b[i]*(b[i]-1)/2);
}
return tmp;
}
int main()
{
// freopen("dp.in","r",stdin);
// freopen("dp.out","w",stdout);
scanf("%d%d",&n,&k);
k--;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
dis[i][j]=solve(i,j);
}
}
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n;i++) f[i][0]=dis[1][i];
for(int i=2;i<=n;i++)
{
for(int j=1;j<i;j++)
{
for(int t=1;t<=k;t++)
{
f[i][t]=min(f[i][t],f[j][t-1]+dis[j+1][i]);
}
}
}
printf("%d",f[n][k]);
return 0;
}
Excellent scale:
#include<iostream>
#include<cstdio>
using namespace std;
const int N=100010;
typedef long long LL;
int c[N],a[N];
LL f[N],g[N];
int p,q,n,k;
LL tot;
void move(int l,int r)
{
while (l<p) p--,tot+=c[a[p]],c[a[p]]++;
while (r>q) q++,tot+=c[a[q]],c[a[q]]++;
while (p<l) c[a[p]]--,tot-=c[a[p]],p++;
while (r<q) c[a[q]]--,tot-=c[a[q]],q--;
}
void work(int l,int r,int fl,int fr)
{
if (fl>fr) return;
int mid=(fl+fr)>>1,mi;
LL mx=1LL<<60;
for (int i=l;i<=r;i++)
if (i<mid)
{
move(i+1,mid);
if (f[i]+tot<mx) mx=f[i]+tot,mi=i;
}
g[mid]=mx;
work(l,mi,fl,mid-1);
work(mi,r,mid+1,fr);
}
int main()
{
freopen("dp.in","r",stdin);
freopen("dp.out","w",stdout);
scanf("%d%d",&n,&k);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
f[0]=0;
for (int i=1;i<=n;i++) f[i]=1LL<<60;
while (k--)
{
p=1,q=0,tot=0;
for (int i=1;i<=n;i++) c[i]=0;
work(0,n-1,1,n);
for (int i=0;i<=n;i++) f[i]=g[i],g[i]=0;
}
cout<<f[n];
return 0;
}