Take you hand in hand to disassemble the LRU algorithm

summary

LRU algorithm is a cache elimination strategy. The principle is not difficult, but it is more skilled to write bug free algorithms in the interview. It needs to abstract and disassemble the data structure layer by layer. labuladong in this paper will write you beautiful code.

The computer's cache capacity is limited. If the cache is full, delete some content and make room for new content. But the question is, what should be deleted? We certainly want to delete the useless cache and keep the useful data in the cache for future use. So, what kind of data do we judge as "useful"?

The full name of LRU is Least Recently Used, that is to say, we think the recently used data should be "useful". The data that has not been used for a long time should be useless. When the memory is full, priority will be given to deleting the data that has not been used for a long time.

For example, Android phones can put software into the background to run. For example, I opened "Settings", "mobile manager" and "calendar" successively. Now their order in the background is as follows:

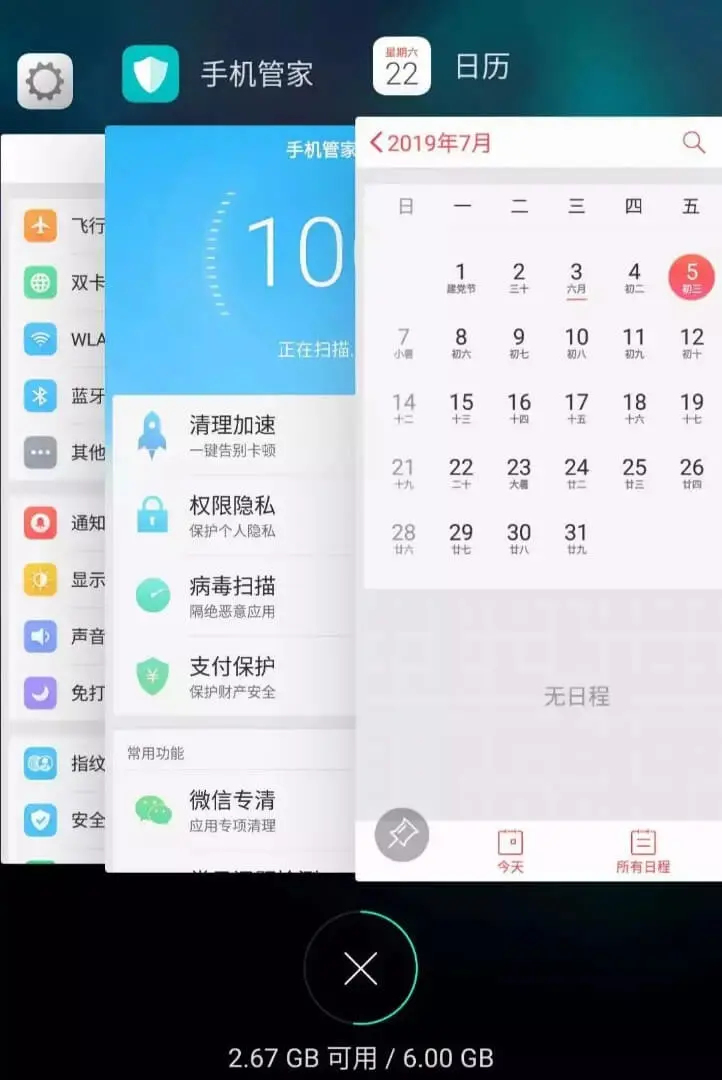
But at this time, if I visit the "Settings" interface, the "Settings" will be advanced to the first one, which will become like this:

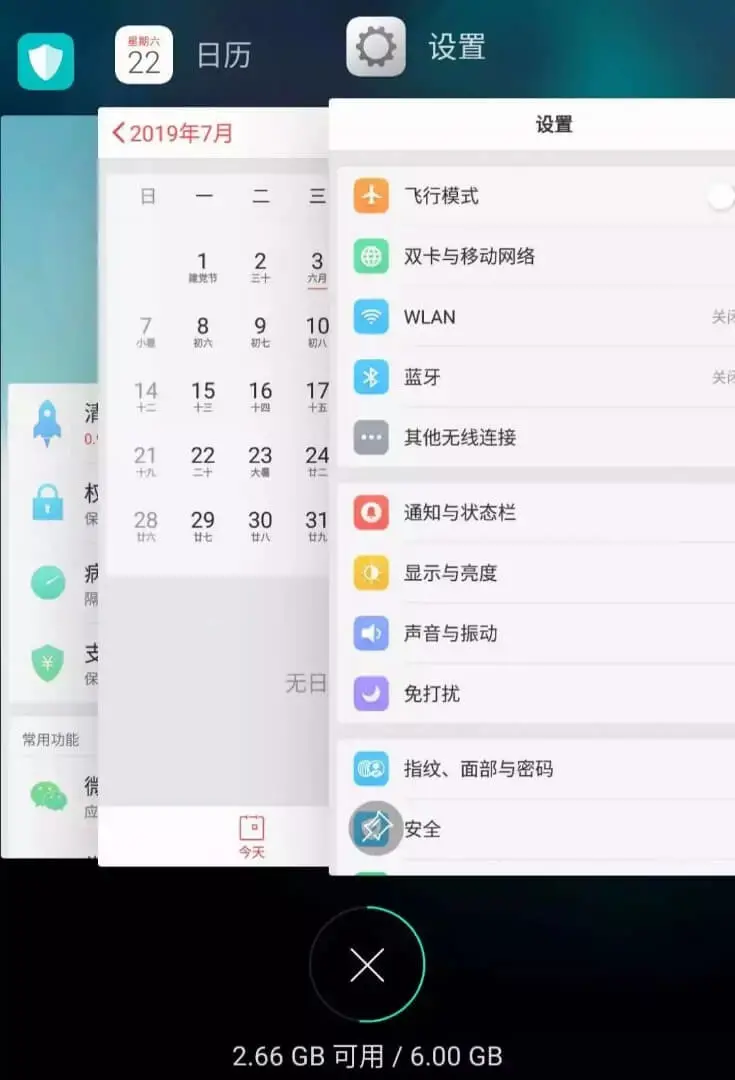
Suppose my phone only allows me to open three applications at the same time, and now it is full. So if I open a new application clock, I have to close an application to make room for the clock. What about closing it?

According to the strategy of LRU, close the "mobile housekeeper" at the bottom, because it has not been used for the longest time, and then put the newly opened application on the top:

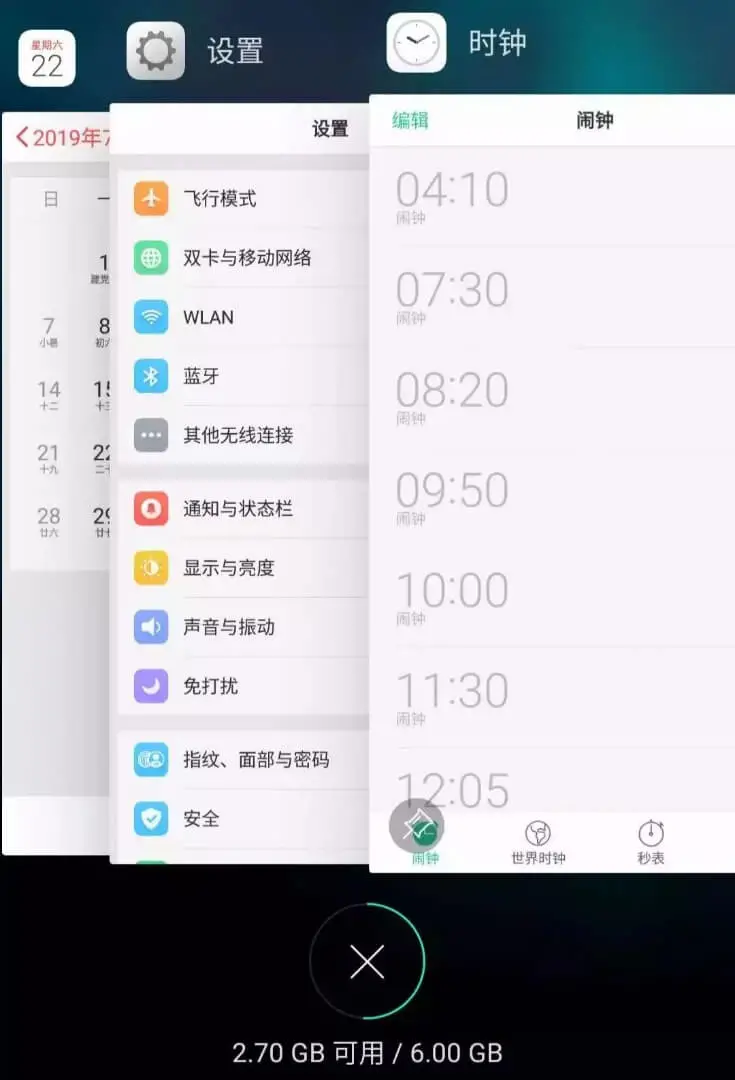
Now you should understand the LRU (Least Recently Used) strategy. Of course, there are other cache elimination strategies, such as not according to the access timing, but according to the access frequency (LFU strategy). Each has its own application scenario. This paper explains the LRU algorithm strategy.

146. LRU cache

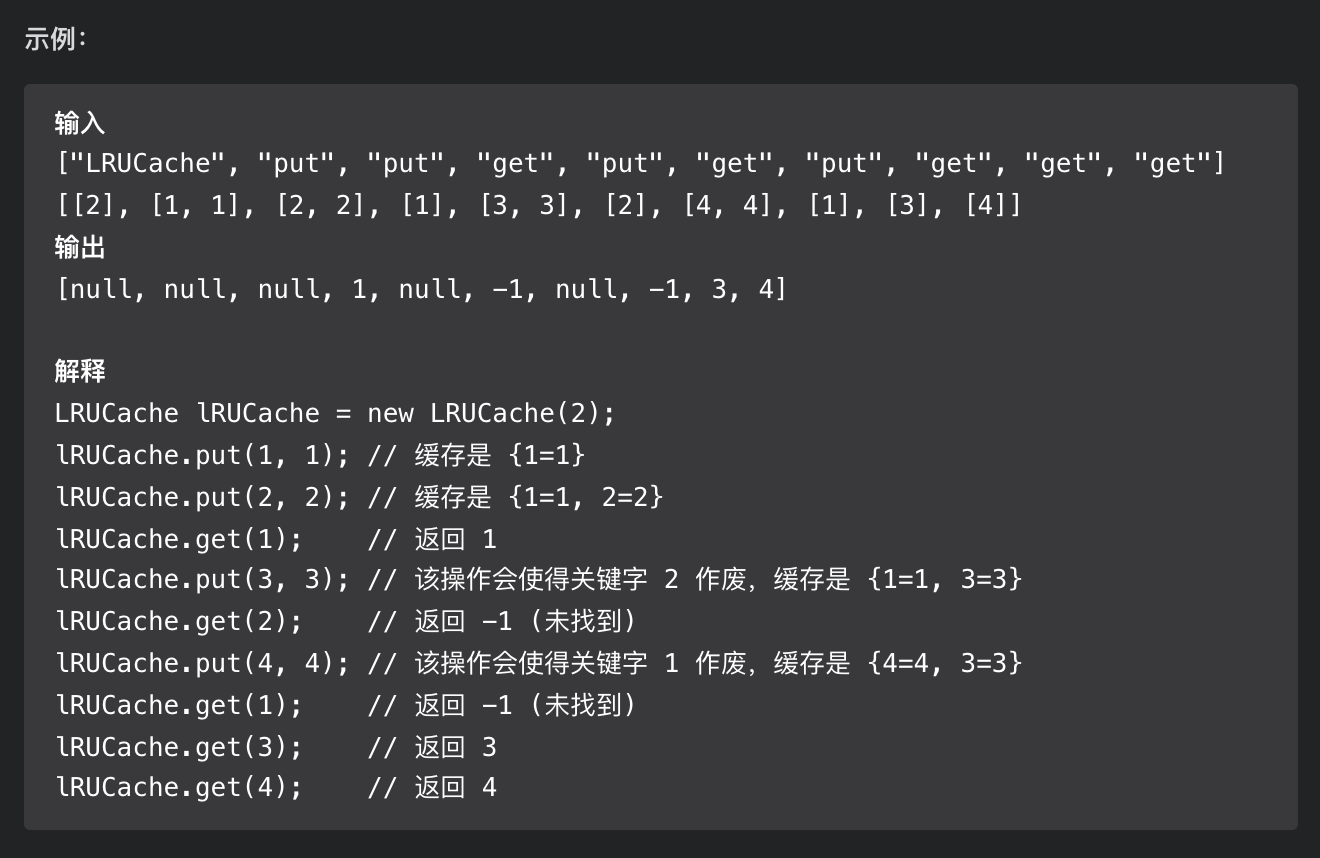
First, you need to receive a capacity parameter as the maximum capacity of the cache, and then implement two API s. One is to store the key value pair with the put(key, val) method, and the other is to get the val corresponding to the key with the get(key) method. If the key does not exist, it returns - 1.

Note that both get and put methods must have O(1) time complexity. Let's take a specific example to see how the LRU algorithm works.

/* The cache capacity is 2 */
LRUCache cache = new LRUCache(2);
// You can think of cache as a queue
// Suppose the left is the head of the team and the right is the tail
// The most recently used ones are at the head of the queue and the ones that have not been used for a long time are at the end of the queue
// Parentheses indicate key value pairs (key, val)

cache.put(1, 1);
// cache = [(1, 1)]

cache.put(2, 2);
// cache = [(2, 2), (1, 1)]

cache.get(1);       // Return 1
// cache = [(1, 1), (2, 2)]
// Explanation: because key 1 was accessed recently, it was advanced to the head of the team
// Returns the value 1 corresponding to key 1

cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// Explanation: the cache capacity is full. You need to delete the content to free up the location
// Give priority to deleting data that has not been used for a long time, that is, data at the end of the team
// Then insert the new data into the head of the team

cache.get(2);       // Return - 1 (not found)
// cache = [(3, 3), (1, 1)]
// Explanation: there is no data with key 2 in the cache

cache.put(1, 4);    
// cache = [(1, 4), (3, 3)]
// Explanation: key 1 already exists. Overwrite the original value 1 with 4
// Don't forget to advance the key value pair to the head of the team

LRU algorithm design

By analyzing the above operation process, to make the time complexity of put and get methods O(1), we can summarize the necessary conditions of cache data structure:

1. Obviously, the elements in the cache must be in chronological order to distinguish between recently used and long unused data. When the capacity is full, delete the location of the longest unused element.

2. We need to quickly find out whether a key already exists in the cache and get the corresponding val;

3. Every time you access a key in the cache, you need to change the element into the most recently used one, that is, the cache should support the rapid insertion and deletion of elements at any location.

So, what data structure meets the above conditions at the same time? Hash table lookup is fast, but the data has no fixed order; The linked list can be divided into order. The insertion and deletion are fast, but the search is slow. So combine it to form a new data structure: hash linked list LinkedHashMap.

The core data structure of LRU caching algorithm is hash linked list, a combination of bidirectional linked list and hash table. The data structure looks like this:

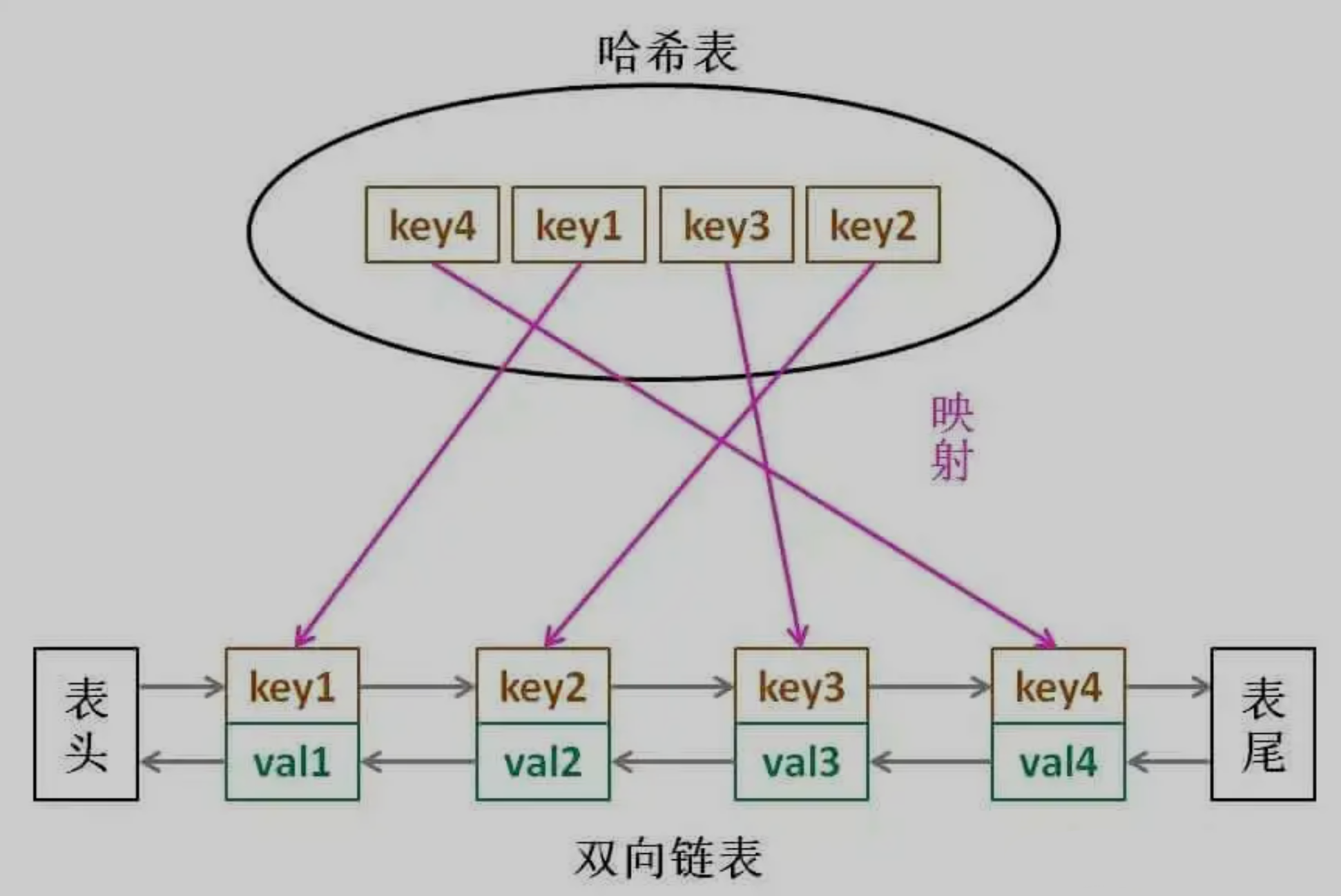
With this structure, we will analyze the above three conditions one by one:

1. If we add elements from the tail of the linked list by default every time, it is obvious that the elements closer to the tail are the most recently used, and the elements closer to the head are the longest unused.

2. For a key, we can quickly locate the node in the linked list through the hash table, so as to obtain the corresponding val.

3. The linked list obviously supports fast insertion and deletion at any position. Just change the pointer. However, the traditional linked list cannot quickly access the elements at a certain location according to the index. Here, with the help of hash table, you can quickly map to any linked list node through key, and then insert and delete.

Perhaps readers will ask, why if it is a two-way linked list, is a single linked list OK? In addition, since the key has been saved in the hash table, why should the key and val be saved in the linked list? Just save Val?

All the time you think is a question, and only when you do can you have an answer. The reason for this design can only be understood after we personally implement the LRU algorithm, so let's start looking at the code

code implementation

Many programming languages have built-in hash linked lists or library functions similar to LRU functions, but in order to help you understand the details of the algorithm, we first build our own wheels to implement the LRU algorithm, and then use the LinkedHashMap built in Java to implement it.

First, we write out the node class of the double linked list. For simplicity, both key and val are considered as int types:

class Node {
    public int key, val;
    public Node next, prev;
    public Node(int k, int v) {
        this.key = k;
        this.val = v;
    }
}

Then build a double linked list based on our Node type to implement several API s necessary for LRU algorithm:

class DoubleList {  
    // Head tail virtual node
    private Node head, tail;  
    // Number of linked list elements
    private int size;

    public DoubleList() {
        // Initialize the data of the two-way linked list
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head.next = tail;
        tail.prev = head;
        size = 0;
    }

    // Add node x at the end of the linked list, time O(1)
    public void addLast(Node x) {
        x.prev = tail.prev;
        x.next = tail;
        tail.prev.next = x;
        tail.prev = x;
        size++;
    }

    // Delete the X node in the linked list (x must exist)
    // Since it is a double linked list and the target Node is given, time O(1)
    public void remove(Node x) {
        x.prev.next = x.next;
        x.next.prev = x.prev;
        size--;
    }

    // Delete the first node in the linked list and return it, time O(1)
    public Node removeFirst() {
        if (head.next == tail)
            return null;
        Node first = head.next;
        remove(first);
        return first;
    }

    // Return the length of the linked list, time O(1)
    public int size() { return size; }

}

Here we can answer the question "why do we have to use a two-way linked list" just now, because we need to delete. Deleting a node not only needs to get the pointer of the node itself, but also needs to operate the pointer of its precursor node. The two-way linked list can support direct search of precursors and ensure the time complexity of operation O(1).

Note that the double linked list API we implemented can only be inserted from the tail, that is, the data near the tail is the most recently used, and the data near the head is the longest used.

With the implementation of bidirectional linked list, we only need to combine it with hash table in LRU algorithm, and build the code framework first:

class LRUCache {
    // key -> Node(key, val)
    private HashMap<Integer, Node> map;
    // Node(k1, v1) <-> Node(k2, v2)...
    private DoubleList cache;
    // Maximum capacity
    private int cap;

    public LRUCache(int capacity) {
        this.cap = capacity;
        map = new HashMap<>();
        cache = new DoubleList();
    }

Don't panic to implement the get and put methods of LRU algorithm. Because we need to maintain a double linked list cache and a hash table map at the same time, it is easy to miss some operations. For example, when deleting a key, we delete the corresponding Node in the cache, but forget to delete the key in the map.

The effective way to solve this problem is to provide a layer of abstract API on top of these two data structures.

It's a little mysterious. In fact, it's very simple, that is, try to make the main methods of LRU get and put avoid directly operating the details of map and cache. We can implement the following functions first:

/* Promote a key to the most recently used */
private void makeRecently(int key) {
    Node x = map.get(key);
    // First delete this node from the linked list
    cache.remove(x);
    // Back at the end of the line
    cache.addLast(x);
}

/* Add recently used elements */
private void addRecently(int key, int val) {
    Node x = new Node(key, val);
    // The tail of the linked list is the most recently used element
    cache.addLast(x);
    // Don't forget to add the key mapping in the map
    map.put(key, x);
}

/* Delete a key */
private void deleteKey(int key) {
    Node x = map.get(key);
    // Delete from linked list
    cache.remove(x);
    // Remove from map
    map.remove(key);
}

/* Delete the longest unused element */
private void removeLeastRecently() {
    // The first element in the head of the linked list is the one that has not been used for the longest time
    Node deletedNode = cache.removeFirst();
    // At the same time, don't forget to delete its key from the map
    int deletedKey = deletedNode.key;
    map.remove(deletedKey);
}

Here we can answer the previous question "why should we store key and val in the linked list at the same time, rather than just Val". Note that in the removeLeastRecently function, we need to use deletedNode to get deletedKey.

In other words, when the cache capacity is full, we should not only delete the last Node, but also delete the key mapped to the Node in the map at the same time, and this key can only be obtained by the Node. If only val is stored in the Node structure, we cannot know what the key is, and we cannot delete the key in the map, resulting in an error.

The above methods are simple operation encapsulation. Calling these functions can avoid directly operating the cache linked list and map hash table. Let me first implement the get method of LRU algorithm:

public int get(int key) {
    if (!map.containsKey(key)) {
        return -1;
    }
    // Promote this data to the most recently used
    makeRecently(key);
    return map.get(key).val;
}

The put method is a little more complicated. Let's draw a diagram to clarify its logic:

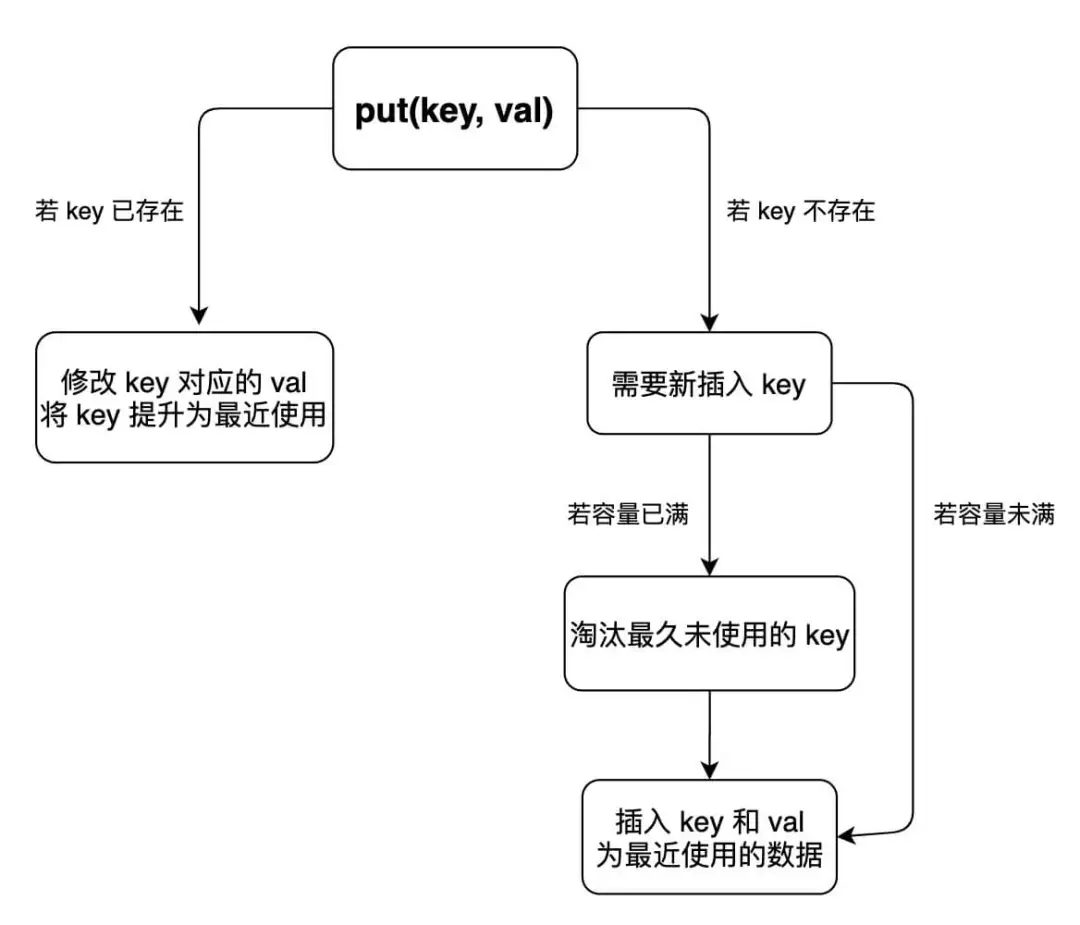
In this way, we can easily write the code of the put method:

public void put(int key, int val) {
    if (map.containsKey(key)) {
        // Delete old data
        deleteKey(key);
        // The newly inserted data is the most recently used data
        addRecently(key, val);
        return;
    }

    if (cap == cache.size()) {
        // Delete the longest unused element
        removeLeastRecently();
    }
    // Add as recently used element
    addRecently(key, val);
}

By now, you should have fully mastered the principle and implementation of LRU algorithm

Complete implementation code

/**
 * @author xiexu
 * @create 2022-01-26 11:05 morning
 */
public class _146_LRU cache {

}

class Node {
    public int key, val;
    public Node next, prev;

    public Node(int k, int v) {
        this.key = k;
        this.val = v;
    }
}

class DoubleList {
    // Head tail virtual node
    private Node head, tail;
    // Number of linked list elements
    private int size;

    public DoubleList() {
        // Initialize the data of the two-way linked list
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head.next = tail;
        tail.prev = head;
        size = 0;
    }

    // Add node x at the end of the linked list, time complexity O(1)
    public void addLast(Node x) {
        x.prev = tail.prev;
        x.next = tail;
        tail.prev.next = x;
        tail.prev = x;
        size++;
    }

    // Delete the X node in the linked list (x must exist)
    // Since it is a double linked list and the target Node is given, time O(1)
    public void remove(Node x) {
        x.prev.next = x.next;
        x.next.prev = x.prev;
        size--;
    }

    // Delete the first node in the linked list and return it, time O(1)
    public Node removeFirst() {
        if (head.next == tail) {
            return null;
        }
        Node first = head.next;
        remove(first);
        return first;
    }

    // Return the length of the linked list, time O(1)
    public int size() {
        return size;
    }

}

class LRUCache {

    // key -> Node(key, val)
    private HashMap<Integer, Node> map;
    // Node(k1, v1) <-> Node(k2, v2)...
    private DoubleList cache;
    // Maximum capacity
    private int cap;

    public LRUCache(int capacity) {
        this.cap = capacity;
        map = new HashMap<>();
        cache = new DoubleList();
    }

    public int get(int key) {
        if (!map.containsKey(key)) {
            return -1;
        }
        // Promote this data to the most recently used
        makeRecently(key);
        return map.get(key).val;
    }

    public void put(int key, int value) {
        if (map.containsKey(key)) {
            // Delete old data
            deleteKey(key);
            // The newly inserted data is the most recently used data
            addRecently(key, value);
            return;
        }
        if (cap == cache.size()) {
            // Delete the longest unused element
            removeLeastRecently();
        }
        // Add as recently used element
        addRecently(key, value);
    }

    /* Promote a key to the most recently used */
    private void makeRecently(int key) {
        Node x = map.get(key);
        // First delete this node from the linked list
        cache.remove(x);
        // Back at the end of the line
        cache.addLast(x);
    }

    /* Add recently used elements */
    private void addRecently(int key, int val) {
        Node x = new Node(key, val);
        // The tail of the linked list is the most recently used element
        cache.addLast(x);
        // Don't forget to add the key mapping in the map
        map.put(key, x);
    }

    /* Delete a key */
    private void deleteKey(int key) {
        Node x = map.get(key);
        // Delete from linked list
        cache.remove(x);
        // Remove from map
        map.remove(key);
    }

    /* Delete the longest unused element */
    private void removeLeastRecently() {
        // The first element in the head of the linked list is the one that has not been used for the longest time
        Node deletedNode = cache.removeFirst();
        // At the same time, don't forget to delete its key from the map
        int deletedKey = deletedNode.key;
        map.remove(deletedKey);
    }

}

The built-in type LinkedHashMap of Java implements the LRU algorithm

class LRUCache {

    int cap;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();

    public LRUCache(int capacity) {
        this.cap = capacity;
    }

    public int get(int key) {
        if (!cache.containsKey(key)) {
            return -1;
        }
        // Change key to recent use
        makeRecently(key);
        return cache.get(key);
    }

    public void put(int key, int value) {
        if (cache.containsKey(key)) {
            // Modify the value of key
            cache.put(key, value);
            // Change key to recent use
            makeRecently(key);
            return;
        }

        if (cache.size() >= this.cap) {
            // The head of the linked list is the longest unused key
            int oldestKey = cache.keySet().iterator().next();
            cache.remove(oldestKey);
        }
        // Add the new key to the end of the linked list
        cache.put(key, value);
    }

    /* Promote a key to the most recently used */
    private void makeRecently(int key) {
        int val = cache.get(key);
        // Delete the key and reinsert it at the end of the queue
        cache.remove(key);
        cache.put(key, val);
    }

}