Tarjan algorithm cut point and Bridge

Posted by Studio381 on Sat, 11 Apr 2020 07:28:02 +0200

1, Tarjan cut point

For undirected graph G, if the number of connected components increases after deleting a point x, then point x is the cut point of graph G.

How to find the cutting point? A simple method is to enumerate each point, delete it and use DFS to find the connected component, so the time complexity is O(nm), which is obviously not very good.

We call the point set of subtree (excluding a) whose root is node a as S(a), and the point set of subtree whose root is not node a as T(a).

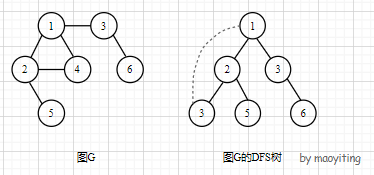
As shown in the figure, if point 2 is deleted, point 4 can be connected with T(2) through the atavism edge in S(2), and deletion 2 has no effect on it; however, point 5 in S(2) is not connected with T(2) because point 5 has no atavism edge, that is, point 2 is a cut point.

In conclusion, the following conclusions are drawn:

For a point x, if there is at least one point y in S(x), and there is no edge between Y and T(x), then x is the cut point.

Specifically, we can use Tarjan algorithm to record dfn[x] and low[x]. So the question turns to whether node X has a son y, making low[y] ≥ dfn[x]. We only need DFS once, the total time complexity O(n+m).

Note: the root must be judged individually, and the root must have at least two subtrees to be counted as the cut point.

The reference procedure is as follows:

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int N=1e5+5;
 5 int n,m,x,y,cnt=1,hd[N],to[N<<1],nxt[N<<1],dfn[N],low[N],num,root;
 6 bool g[N];
 7 void add(int x,int y){
 8     to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
 9 }
10 void tarjan(int x){
11     dfn[x]=low[x]=++num;
12     int flag=0;
13     for(int i=hd[x];i;i=nxt[i]){
14         int y=to[i];
15         if(!dfn[y]){
16             tarjan(y),low[x]=min(low[x],low[y]);
17             if(low[y]>=dfn[x]){
18                 flag++;
19                 if(x!=root||flag>1) g[x]=1;
20             }
21         }
22         else low[x]=min(low[x],dfn[y]);
23     }
24 }
25 signed main(){
26     //freopen(".in","r",stdin);
27     //freopen(".out","w",stdout);
28     scanf("%lld%lld",&n,&m);
29     for(int i=1;i<=m;i++){
30         scanf("%lld%lld",&x,&y);
31         if(x==y) continue;
32         add(x,y),add(y,x);
33     }
34     for(int i=1;i<=n;i++)
35         if(!dfn[i]) root=i,tarjan(i);
36     for(int i=1;i<=n;i++)
37         if(g[i]) printf("%lld ",i);    //The output is the cut point 
38     return 0;
39 }

2, Tarjan cut edge

Bridge (cut edge): in undirected connected graph, if an edge is removed and the number of connected components in the graph increases, then this edge is called bridge or cut edge.

Judgment bridge: an undirected edge (x,y) is a bridge, if and only if (x,y) is a branch edge, and satisfies DFN (x) < low (y). (because y's father who wants to reach X has to pass (x,y) this edge, so delete this edge, the graph is not connected.).

Because it traverses undirected graph, its parent node fa can always be accessed from every point X. According to the calculation method of low, (x,fa) belongs to the edge of the search tree, and fa is not a child node of X, so the time stamp of fa cannot be used to update low[x].

If you record only the parent nodes of each node, you will not be able to handle heavy edges. When there are multiple sides between X and fa, (x,fa) must not be a bridge. Among these repeated edges, only one is "edge on search tree", and the others are not. Therefore, dfn[fa] can be used to update low[x] when there are multiple edges.

Change to record "number of edges recursively entering each node". The number can be considered as the subscript position of the edge stored in the adjacency table. Each edge of an undirected graph is treated as a two-way edge and stored in a pair of subscripts. If the node x is recursively entered along the edge numbered i, the edge numbered i xor 1 starting from X is ignored, and low[x] can be calculated by other edges.

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int N=1e5+5;
 5 int n,m,x,y,cnt=1,hd[N],to[N<<1],nxt[N<<1],dfn[N],low[N],num;
 6 bool g[N<<1];
 7 void add(int x,int y){
 8     to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
 9 }
10 void tarjan(int x,int fa){
11     dfn[x]=low[x]=++num;
12     for(int i=hd[x];i;i=nxt[i]){
13         int y=to[i];
14         if(!dfn[y]){
15             tarjan(y,i);
16             low[x]=min(low[x],low[y]);
17             if(low[y]>dfn[x]) g[i]=g[i^1]=1;
18         }
19         else if(i!=(fa^1)) low[x]=min(low[x],dfn[y]);
20     }
21 }
22 signed main(){
23     //freopen(".in","r",stdin);
24     //freopen(".out","w",stdout);
25     scanf("%lld%lld",&n,&m);
26     for(int i=1;i<=m;i++){
27         scanf("%lld%lld",&x,&y);
28         add(x,y),add(y,x);
29     }
30     for(int i=1;i<=n;i++)
31         if(!dfn[i]) tarjan(i,0);
32     for(int i=2;i<cnt;i+=2)
33         if(g[i]) printf("%lld %lld\n",to[i^1],to[i]);
34     return 0;
35 }

III. examples

Luogu P1656 explosion Railway

Title Link Idea: cut edge directly, and then sort.

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int N=1e5+5;
 5 int n,m,x,y,cnt=1,hd[N],to[N<<1],nxt[N<<1],dfn[N],low[N],num,sum;
 6 bool g[N<<1];
 7 struct data{
 8     int x,y;
 9 }a[N];
10 bool cmp(data x,data y){
11     if(x.x!=y.x) return x.x<y.x;
12     return x.y<y.y;
13 } 
14 void add(int x,int y){
15     to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
16 }
17 void tarjan(int x,int fa){
18     dfn[x]=low[x]=++num;
19     for(int i=hd[x];i;i=nxt[i]){
20         int y=to[i];
21         if(!dfn[y]){
22             tarjan(y,i);
23             low[x]=min(low[x],low[y]);
24             if(low[y]>dfn[x]) g[i]=g[i^1]=1;
25         }
26         else if(i!=(fa^1)) low[x]=min(low[x],dfn[y]);
27     }
28 }
29 signed main(){
30     //freopen(".in","r",stdin);
31     //freopen(".out","w",stdout);
32     scanf("%lld%lld",&n,&m);
33     for(int i=1;i<=m;i++){
34         scanf("%lld%lld",&x,&y);
35         add(x,y),add(y,x);
36     }
37     for(int i=1;i<=n;i++)
38         if(!dfn[i]) tarjan(i,0);
39     for(int i=2;i<cnt;i+=2)
40         if(g[i]) a[++sum]=(data){to[i^1],to[i]};
41     sort(a+1,a+1+sum,cmp);
42     for(int i=1;i<=sum;i++){ 
43         if(a[i].x>a[i].y) swap(a[i].x,a[i].y);
44         printf("%lld %lld\n",a[i].x,a[i].y);
45     } 
46     return 0;
47 }

Luogu P3388 "template" cut point (cut top)

Title Link Idea: Board questions. Direct code:

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 using namespace std;
 4 const int N=1e5+5;
 5 int n,m,x,y,cnt=1,hd[N],to[N<<1],nxt[N<<1],dfn[N],low[N],num,root,sum;
 6 bool g[N];
 7 void add(int x,int y){
 8     to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
 9 }
10 void tarjan(int x){
11     dfn[x]=low[x]=++num;
12     int flag=0;
13     for(int i=hd[x];i;i=nxt[i]){
14         int y=to[i];
15         if(!dfn[y]){
16             tarjan(y),low[x]=min(low[x],low[y]);
17             if(low[y]>=dfn[x]){
18                 flag++;
19                 if(x!=root||flag>1) g[x]=1;
20             }
21         }
22         else low[x]=min(low[x],dfn[y]);
23     }
24 }
25 signed main(){
26     //freopen(".in","r",stdin);
27     //freopen(".out","w",stdout);
28     scanf("%lld%lld",&n,&m);
29     for(int i=1;i<=m;i++){
30         scanf("%lld%lld",&x,&y);
31         if(x==y) continue;
32         add(x,y),add(y,x);
33     }
34     for(int i=1;i<=n;i++)
35         if(!dfn[i]) root=i,tarjan(i);
36     for(int i=1;i<=n;i++)
37         if(g[i]) sum++;
38     printf("%lld\n",sum);
39     for(int i=1;i<=n;i++)
40         if(g[i]) printf("%lld ",i);
41     return 0;
42 }