Template Title Link
- BST Lookup- Leetcode 270. Closest BST Value
- BST Insert- Leetcode 701. Insert Node in BST
- BST Delete- Leetcode 450. Delete Node in BST
Binary Search Tree-BST Overview
BST is a kind of binary tree, which has the structural properties of binary tree: there is only one Root node, each node can have at most two left and right sub-nodes. The nature of BST itself: the left son value of each node must be smaller than him, and the right son value must be larger than him. This property also makes the intermediate traversal output of BST a strictly increasing sequence. Strictly, elements with the same numeric value are not saved in BST, and if there are duplicate elements, count attributes can be added to each node to count them.
BST Basic Question Template
- Find an element
Based on the relationship between the size of the left and right child nodes of BST, the numerical query can be done directly by using the dichotomy method. If the current value is smaller than the value of the lookup, then look to the left and vice versa.
The code is as follows:
class Solution {
double min = Double.MAX_VALUE;
int res = -1;
public int closestValue(TreeNode root, double target) {
search(root, target);
return res;
}
private void search(TreeNode root, double target) {
// > The first number of targets
if(root==null) return;
if(Math.abs(root.val-target)<min) {
min = Math.abs(root.val-target);
res = root.val;
}
if(root.val>target) search(root.left, target);
search(root.right, target);
}
}Time Complexity: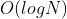 If the BST structure is more balanced (maximum height difference <=1), that is, when the BST is balanced, it is possible that the BST structure is very unbalanced, that is, all nodes form a similar chain table structure, and the time will be
If the BST structure is more balanced (maximum height difference <=1), that is, when the BST is balanced, it is possible that the BST structure is very unbalanced, that is, all nodes form a similar chain table structure, and the time will be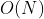 ; Spatial Complexity:
; Spatial Complexity: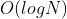 That is, the depth of recursion. (
That is, the depth of recursion. (
- BST Insert Node
The idea of inserting nodes is more understandable. First, we find the position of leaf nodes that can be inserted according to the size relationship and establish a new node to connect with BST.
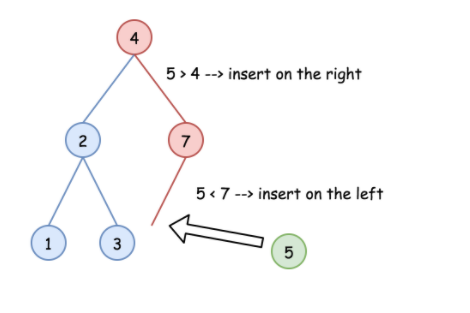 Insert a diagram from:
Leetcode Solution
Insert a diagram from:
Leetcode Solution
The code is as follows:
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
TreeNode res = insert(root, val);
return res;
}
private TreeNode insert(TreeNode root, int val){
// Divide and Conquer
if(root==null) return new TreeNode(val);
if(root.val<val) root.right = insert(root.right, val);
else if(root.val>val) root.left = insert(root.left, val);
return root;
}
}- Delete Node
Deleting a node is the most complex of the basic queries because when deleting an element, in order to maintain the orderly nature of the BST, you need to find a node to replace the deleted node location and ensure that it remains BST after the substitution.
There are three possibilities when removing a node:
- Delete node is a leaf node: in this case, delete the node directly
- Deleting a node has only a left or right son: in this case, the left or right son of the deleting node can be directly connected
- Delete nodes have left and right sons: This is the most complex case, and two types of nodes are usually found as substitutes: the largest point in the left subtree, or the smallest point in the right subtree - the predecessor and successor of the delete point. These two points are usually leaf nodes or have only left or right sons (since they are themselves the leftmost and right nodes in a subtree), so after replacing the node with the deleted node, connect the left or right subtree directly (if any).
- The largest point of the left subtree: the rightmost point of the left subtree
- The smallest point of the right subtree: the leftmost point of the right subtree
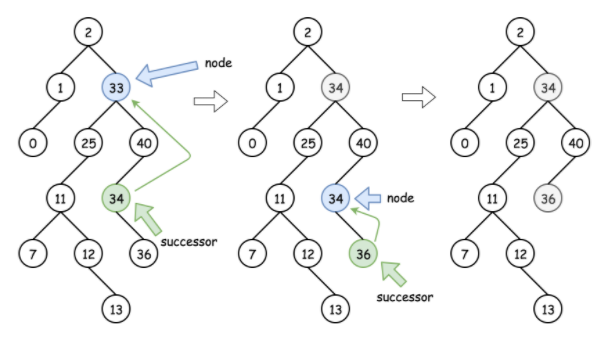 Subsequent Node Substitution Diagram: Source-
Leetcode Solution
Subsequent Node Substitution Diagram: Source-
Leetcode Solution
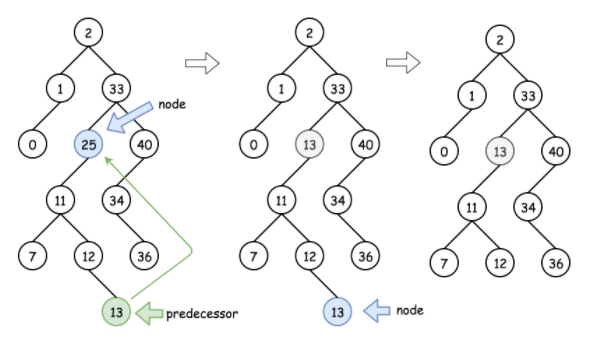 Precursor Node Substitution Diagram: Source-
Leetcode Solution
Precursor Node Substitution Diagram: Source-
Leetcode Solution
The code is as follows:
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
TreeNode res = delete(root, key);
return res;
}
private TreeNode delete(TreeNode root, int key) {
if(root==null) return null;
if(root.val<key) root.right = delete(root.right, key);
else if(root.val>key) root.left = delete(root.left, key);
else {
// if root is leaf, directly remove
if(root.left==null && root.right==null) {
return null;
} else if(root.left!=null && root.right!=null) {
// find predecessor or successor to replace remove node
// predecessor - Maximum on the left
TreeNode left = root.left;
if(left.right==null) {
// no right node current node is predecessor
root.val = left.val;
root.left = left.left;
} else {
// Find the rightmost, that is, the largest node and parent of the largest node, to the right
// Use the slow and fast pins here to find the corresponding position
TreeNode fast = left.right;
TreeNode slow = left;
while(fast.right!=null) {
fast = fast.right;
slow = slow.right;
}
// fast finds the rightmost, slow is the last node
root.val = fast.val;
slow.right = fast.left; // remove predecessor
}
return root;
} else {
// one side is not leaf
if(root.left!=null) return root.left;
if(root.right!=null) return root.right;
}
}
return root;
}
}Time Complexity: If BST is balanced then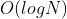 Worst case scenario:
Worst case scenario: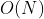 ; Spatial Complexity:
; Spatial Complexity: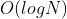 That is, recursion depth. (
That is, recursion depth. (