Recently, a lot of small partners have communicated with me about brushing problems. My advice is to offer and buckle hot100 first. There are still some very important and frequent occurrences in these problems. Today, I share the 10 most frequently occurring arithmetic problems with you, and learn to make money.

 

0X01 Flip Chain List

Force button 206 and sword finger offer 24 origin, meaning:

Give you the head node of the single-chain list, invert the list, and return the inverted list.

Analysis:

Flipping a list means not creating a new list node and then flipping it on the original list, but this graph can be a bit misleading. In fact, you can see the following picture for a better understanding:

 

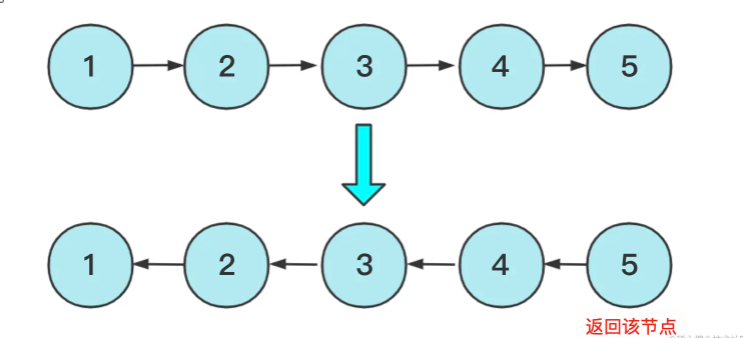
Specifically, there are two ways to achieve the above two ideas, non-recursive and recursive, non-recursive is relatively simple. Using a prenode to record the precursor node, when enumerating down, you can change the pointer pointing, and the implementation code is:

class Solution {
    public ListNode reverseList(ListNode head) {
       if(head==null||head.next==null)//If the node is NULL or a single node returns directly
            return head;
        ListNode pre=head;//Precursor Node
        ListNode cur=head.next;//The current node is used for enumeration
        while (cur!=null)
        {
            ListNode next=cur.next;
            //Change Point
            cur.next=pre;
            pre=cur;
            cur=next;
        }
        head.next=null;//Prevent the last ring by null ing the original head node next
        return pre;
    }
}

Recursion is a clever way to change pointer-to-pointer and return-to-value transfer by using the process of recursion. The code is concise but difficult to understand. Here is a diagram to help you understand:

 

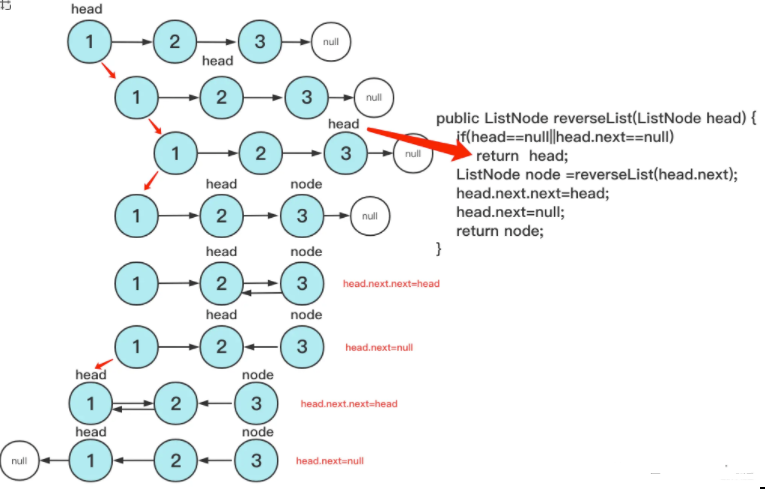
The code is:

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null||head.next==null)//If the last node does not operate
            return  head;
        ListNode node =reverseList(head.next);//Recurse to the bottom and then back
        head.next.next=head;//The next node points to itself
        head.next=null;//next I pointed to was set to null
        return node;//Return to the last node (passed recursively all the time)
    }
}

0X02 Design LRU

For the 146LRU Cache mechanism with the title:

Design and implement an LRU cache mechanism using the data structure you have. Implement the LRUCache class:

LRUCache(int capacity) initializes LRU cache int get(int key) with positive integer capacity capacity. If the key exists in the cache, it returns the value of the key, otherwise it returns -1. void put(int key, int value) If a keyword already exists, change its data value; If the keyword does not exist, insert the group Keyword-Value. When the cache capacity reaches its maximum, it should delete the oldest unused data value before writing new data to make room for new data values.

Advanced: Complete both operations within O(1) time complexity

Detailed Analysis: An Experience in LRU

The core of LRU is to use hash + double-linked list, which is used for query. Double-linked list can delete complex O(1) only if the current node can be deleted. However, special cases of head-end pointer need to be considered for double-linked list.

 

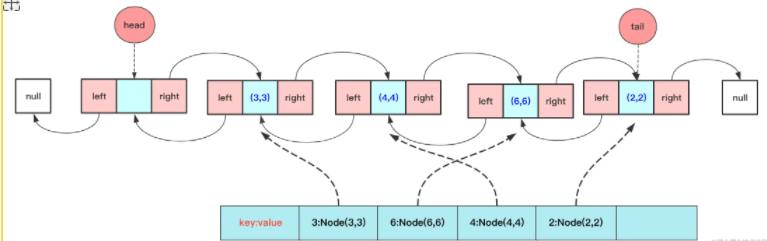
The code for implementation is:

class LRUCache {
    class Node {
        int key;
        int value;
        Node pre;
        Node next;
        public Node() {
        }
        public Node( int key,int value) {
            this.key = key;
            this.value=value;
        }
    }
    class DoubleList{
        private Node head;// Head Node
        private Node tail;// End Node
        private int length;
        public DoubleList() {
            head = new Node(-1,-1);
            tail = head;
            length = 0;
        }
        void add(Node teamNode)// Default End Node Insertion
        {
            tail.next = teamNode;
            teamNode.pre=tail;
            tail = teamNode;
            length++;
        }
        void deleteFirst(){
            if(head.next==null)
                return;
            if(head.next==tail)//If the deleted one happens to be tail-aware, move the tail pointer in front of it
                tail=head;
            head.next=head.next.next;

            if(head.next!=null)
                head.next.pre=head;
            length--;
        }
        void deleteNode(Node team){

            team.pre.next=team.next;
            if(team.next!=null)
                team.next.pre=team.pre;
            if(team==tail)
                tail=tail.pre;
           team.pre=null;
           team.next=null;
            length--;
        }
    }
    Map<Integer,Node> map=new HashMap<>();
    DoubleList doubleList;//Storage Order
    int maxSize;
    LinkedList<Integer>list2=new LinkedList<>();

    public   LRUCache(int capacity) {
        doubleList=new DoubleList();
        maxSize=capacity;
    }
    public int get(int key) {
        int val;
        if(!map.containsKey(key))
            return  -1;
        val=map.get(key).value;
        Node team=map.get(key);
        doubleList.deleteNode(team);
        doubleList.add(team);
        return  val;
    }

    public void put(int key, int value) {
        if(map.containsKey(key)){// There is already this key deleted and updated regardless of length
           Node deleteNode=map.get(key);
            doubleList.deleteNode(deleteNode);
        }
        else if(doubleList.length==maxSize){//Not included and less than length
            Node first=doubleList.head.next;
            map.remove(first.key);
            doubleList.deleteFirst();
        }
       Node node=new Node(key,value);
        doubleList.add(node);
        map.put(key,node);

    }
}

0X03 Ring Chain List

For stress buckle 141 and force buckle 142, force buckle 141 ring list requirements are:

Given a list of chains, determine if there are rings in the list, and use O(1) memory to solve.

Detailed analysis: It's great to find the entrance to the ring list

This problem is more efficient using fast and slow double pointer, fast pointer fast takes 2 steps at a time, slow takes 1 step at a time, slow pointer takes 2 N steps at the end of n step, and the size of the ring must be less than or equal to n so it must meet. If it meets, it means there are rings. If it does not meet, fast first indicates no rings for null.

The code is:

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast=head;
        ListNode slow=fast;
        while (fast!=null&&fast.next!=null) {
            slow=slow.next;
            fast=fast.next.next;
            if(fast==slow)
                return true;
        }
        return false;    
    }
}

Force buckle 142 is extended by force buckle 141. If there is a ring, return to the node that enters the ring, think of node 2 in the ring chain table in the following figure.

 

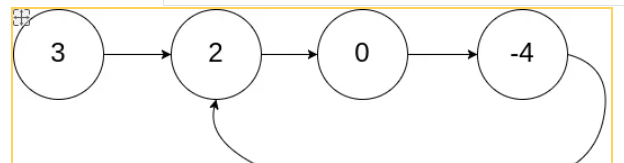
This problem requires a mathematical conversion. The detailed analysis can be seen above. Here are the steps for the main topic.

If the first junction is found, one stops and the other continues, and the next junction happens to take a circle, the length of the loop can be calculated as y.

So what we know is that at the junction, fast takes 2x steps, slow takes x steps, and the ring length is y. And when the fast pointer and the slow pointer intersect, the number of extra steps is just an integer multiple of the length y (it's at the same location at the moment, and the fast pointer just a lot of circles around integers can meet at the same location), and you get 2x=x+ny(x=ny). So the X that the slow pointer moves and the X that the fast pointer moves more are integers of the circle length y.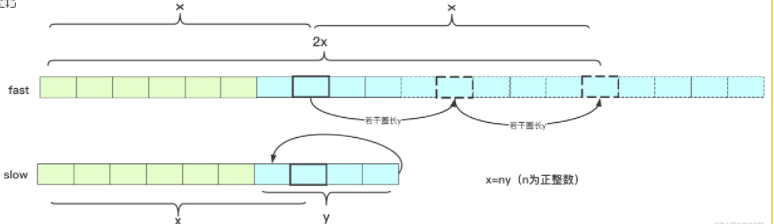

 

That is to say, there are x steps from the beginning to this point, and X steps from this point are also a few rounds back to this point. If slow starts from the starting point and fast starts from this point (one step at a time, equivalent to the distance before two steps offset slow), then x-step will reach this point, but these two pointers are one step at a time, so once slow reaches the circle, the two pointers begin to converge.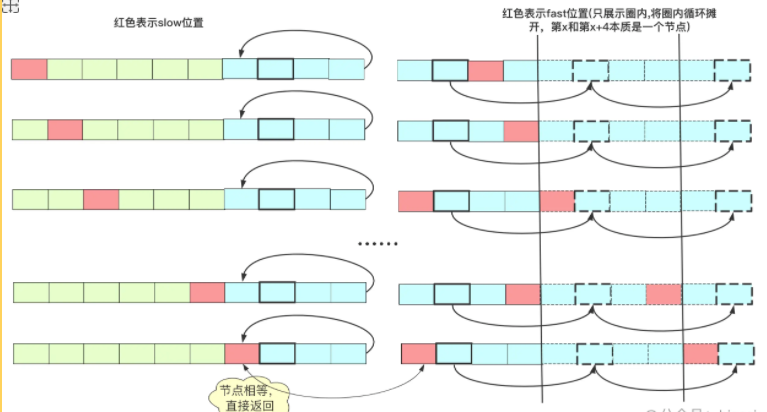

 

The implementation code is:

public class Solution {
    public ListNode detectCycle(ListNode head) {
	    boolean isloop=false;
		ListNode fast=new ListNode(0);//Head Pointer
		ListNode slow=fast;
		fast.next=head;
		if(fast.next==null||fast.next.next==null)
			return null;
		while (fast!=null&&fast.next!=null) {
			fast=fast.next.next;
			slow=slow.next;
			if(fast==slow)
			{
				isloop=true;
				break;
			}
		}
		if(!isloop)//If no loops return
			return null;
		ListNode team=new ListNode(-1);//Next to the head pointer is the head
		team.next=head;
		while (team!=fast) {//slow and fast start from the start and current point, respectively
			team=team.next;
			fast=fast.next;
		}
		return team;
    }
}

0X04 Two Stacks Implement Queue

The corresponding sword finger offer 09 is titled:

Implement a queue with two stacks. The queue is declared as follows. Implement its two functions appendTail and deleteHead to insert integers at the end of the queue and delete integers at the head of the queue, respectively. (deleteHead returns -1 if there are no elements in the queue)

Analysis:

To solve this problem, you need to know what the stack is, what the queue is, and what the two common data structure formats are simple. The stack features are: LIFO, the queue features are: FIFO, the stack can be imagined as a stack of books, the sooner the stack is fetched, the above comes out (for example); Queues are imagined to be queued for shopping, only going in and out from behind, so there are differences in data structure between the two. Although they are all single entries in and out, stack imports and exports are the same, but queues are different.

The data structure described above is a common stack and queue, in which we use two stacks to implement a queue operation. One of the easier scenarios to think about here is that stack1 is used as a data store, stack1 is inserted directly at the end of the insertion, and data is added to another stack2 first when the header is deleted, and the top elements of the stack are returned and deleted. Adding stack2 order to stack 1 implements a recovery, but insertion time complexity is O(1) and deletion time complexity is O(n).

We will also show you how to achieve this:

class CQueue {

    Stack<Integer>stack1=new Stack<>();
    Stack<Integer>stack2=new Stack<>();
    public CQueue() {
    }
    public void appendTail(int value) {
       stack1.push(value);
    }
    public int deleteHead() {
        if(stack1.isEmpty())
            return -1;
       
        while (!stack1.isEmpty())
        {
            stack2.push(stack1.pop());
        }
       int value= stack2.pop();
        while (!stack2.isEmpty())
        {
            stack1.push(stack2.pop());
        }
        return  value;
    }
}

This kind of time complexity is not like, because deleting is too time consuming and has to be tossed around every time. Is there any good way to make deletion easier?

Yes, stack1 guarantees sequential insertion, and stack1 data can be deleted in stack2. So stack1 is used for insertion and stack2 is used for deletion, because the title does not require data to be placed in a container, so it's a perfect combination!

 

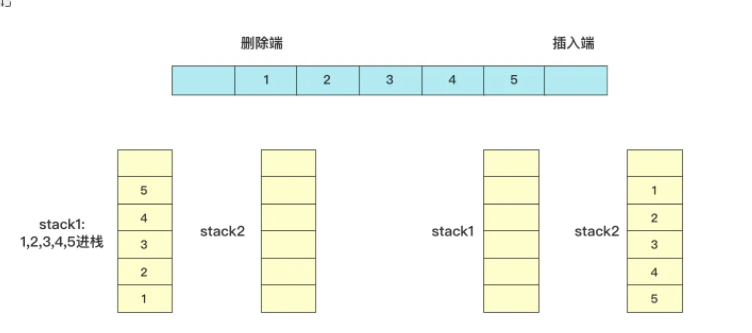
When implementing this, insert directly into stack1, if deletion is required from the top of stack2, if stack2 is empty then add all the data in stack1 (which in turn ensures that all data in stack2 can be deleted sequentially). Here are a few examples of deletion

 

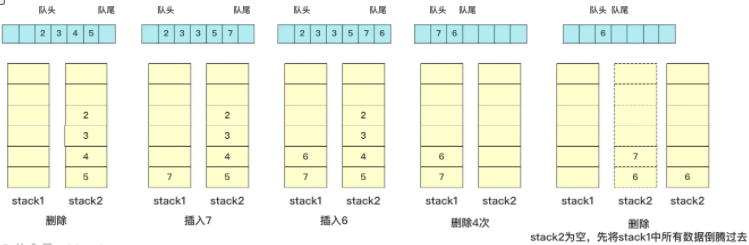
In fact, the data is divided into two parts, one for insertion and one for deletion. The stack2 deleted is empty and the data added in all stack1 is continued to operate. The time complexity of inserting and deleting this operation is O(1), which is implemented in code:

class CQueue {
    Deque<Integer> stack1;
    Deque<Integer> stack2;
    
    public CQueue() {
        stack1 = new LinkedList<Integer>();
        stack2 = new LinkedList<Integer>();
    }
    
    public void appendTail(int value) {
        stack1.push(value);
    }
    
    public int deleteHead() {
        // Add stack1 data to stack2 if the second stack is empty
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        } //No data if stack2 is still empty
        if (stack2.isEmpty()) {
            return -1;
        } else {//Otherwise delete
            int deleteItem = stack2.pop();
            return deleteItem;
        }
    }
}

0X05 Binary Tree Sequence (Sawtooth) Traversal

Traversal of a binary tree, for stress buckles 102, 107, 103.

Detailed analysis: An interview was blown up by binary tree hierarchy traversal

Ordinary binary tree hierarchy traversal is not a difficult problem, but it has a hierarchical operation to return results that you need to consider in detail.

Many people use two containers (queues) for hierarchical operations, where you can actually use a single queue directly. First, we record the queue size len before enumeration, and then enumerate the len to get the complete data for that layer.

Another difficulty is the jagged sequence of binary trees (also known as zigzag printing), the first from left to right and the second from right to left, simply recording the corresponding operations of an even and odd number of layers.

 

 

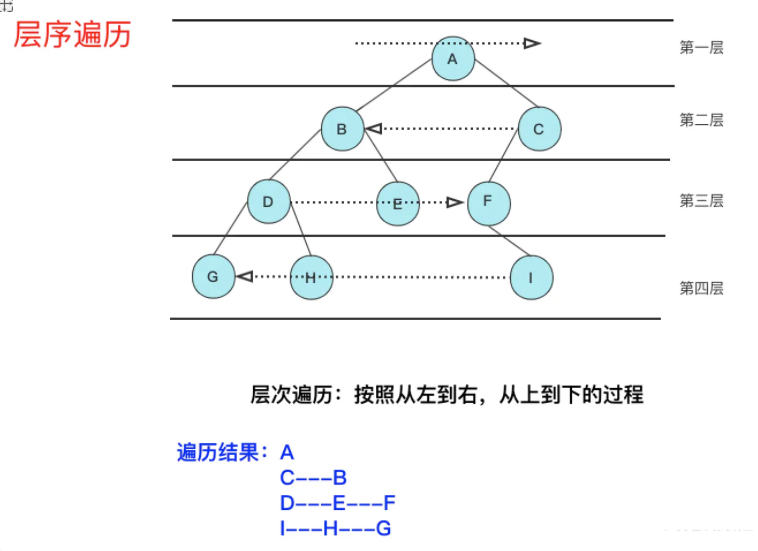
Here we share the code with you by using the jagged sequential traversal of 103 binary trees as a test board:

public List<List<Integer>> levelOrder(TreeNode root) {
  List<List<Integer>> value=new ArrayList<>();//Stored final results
  if(root==null)
    return value;
  int index=0;//judge
  Queue<TreeNode>queue=new ArrayDeque<>();
  queue.add(root);
  while (!queue.isEmpty()){
    List<Integer>va=new ArrayList<>();//Temporarily used for storage in value
    int len=queue.size();//Number of nodes at the current level
    for(int i=0;i<len;i++){
      TreeNode node=queue.poll();
      if(index%2==0)//Add Policy Based on Parity Selection
        va.add(node.val);
      else
        va.add(0,node.val);
      if(node.left!=null)
        queue.add(node.left);
      if(node.right!=null)
        queue.add(node.right);
    }
    value.add(va);
    index++;
  }
  return value;
}

Post-order traversal (non-recursive) in 0X06 binary tree

The non-recursive traversal of binary trees is also the focus of the investigation. For the recursive implementation of middle-order post-order traversal, it is very simple, but the non-recursive implementation is still a key skill.

Detailed analysis: Various traversals of binary trees (recursive, non-recursive)

For the middle traversal of a binary tree, it is normal to throw out the output when the node is visited for the second time (the first prefix), so that we enumerate that each node cannot be deleted for the first time, we need to store it in the stack first, and throw out the access to the node when the left child node is processed.

 

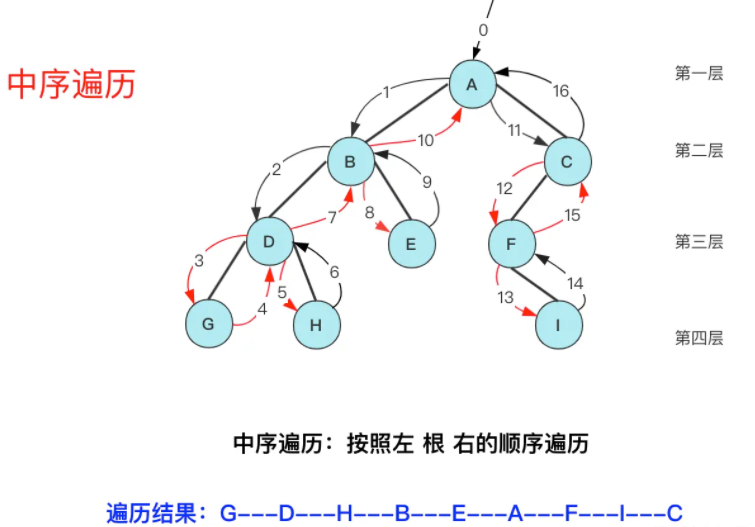
The core is a two-step process, with both left and right leaf nodes null, which also meets the following conditions:

1. The current node is enumerated (no output is stored) and stored in a stack, with the node pointing to the left node until the left child is null.
2. Throw stack top access. If there is a right node, visit its right node and repeat step 1. If there is no right node, continue repeating step 2 throwing.

The implementation code is:

class Solution {
   public List<Integer> inorderTraversal(TreeNode root) {
	List<Integer>value=new ArrayList<Integer>();
    Stack<TreeNode> q1 = new Stack();	
    while(!q1.isEmpty()||root!=null)
    {
        while (root!=null) {
            q1.push(root);				
            root=root.left;
        }
        root=q1.pop();//Throw
        value.add(root.val);
        root=root.right;//Ready to access its right node
        
    }
    return value;
  }
}

Then traversal follows a recursive thinking, in fact, the third visit to the node is usually to throw the output from the right child node, which is really difficult to achieve. However, for the specific implementation, we use a prenode to record the last point that was thrown. If the right child being thrown is preor the right node is null, throw this point out. Otherwise, the right side of the prenode has not been visited and needs to be "rebuilt" for later use! If you don't understand this, you can see the details above.

The code for implementation is:

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        TreeNode temp=root;//Temporary nodes enumerated
        List<Integer>value=new ArrayList<>();
        TreeNode pre=null;//Pre-Node
        Stack<TreeNode>stack=new Stack<>();

        while (!stack.isEmpty()||temp!=null){
        
            while(temp!=null){
                stack.push(temp);
                temp=temp.left;
            }
            temp=stack.pop();
            if(temp.right==pre||temp.right==null)//Eject Required
            {
                value.add(temp.val);
                pre=temp;
                temp=null;//Need to re-throw from stack
            }else{
                stack.push(temp);
                temp=temp.right;
            }
            
        }
        return value;
    }
}

Of course, post-order traversal can also be useful if the results of the pre-order traversal of the preceding order (right-left root) are flipped one last time, but the interviewer prefers to look at the method mentioned above.

0X07 Step Jump (Fibonacci, Stair Climb)

Climbing stairs and jumping steps is a classical problem. It corresponds to offer10 of swordfinger and 70 questions of forceful buckle. The Title is:

Suppose you are climbing the stairs. You need n steps to reach the roof. You can climb one or two steps at a time. How many different ways do you have to climb to the top?** Note: ** Given n n n is a positive integer.

Analysis:

This question starts at level dp and analyses the results of the current k-th order. Each person can climb one or two steps, so it may be from k-1 or k-2, so it is the overlap of two sub-situations (special consideration is needed for the initial situation). Recursion is thought of by some people. Yes, recursion does work, but it's less efficient (since this is a divergent recursion that splits into two), and it's slightly better to use a memory search.

However, DP is a better method. The core state transfer equation is: dp[i]=dp[i-1]+dp[i-2]. Some spatial optimizations are better because only the first two values are used, so you can use three values repeatedly to save space.

class Solution {
    public int climbStairs(int n) {
        if(n<3)return n;
		 int dp[]=new int[n+1];
		 dp[1]=1;
		 dp[2]=2;
		 for(int i=3;i<n+1;i++)
		 {
			 dp[i]=dp[i-1]+dp[i-2];
		 }
		 return dp[n];
    }
  
  public int climbStairs(int n) {
        int a = 0, b = 0, c = 1;
        for (int i = 1; i <= n; i++) {
            a = b; 
            b = c; 
            c = a + b;
        }
        return c;
    }
}

Of course, some of the data is very redundant step, can be solved by the matrix power quickly, but this is not introduced here, interested can have a detailed look.

0X08 TOPK Problem

The TOPK question is really classical. It usually asks the smallest number of K. Looking for K is mostly TOPK. Here, 215 is buckled to look for the K big element of the array as the board.

Detailed analysis: One article pinches TOPK

TOPK has a lot of ideas for problem solving. If the optimized bubble or simple selection sort, the time complexity is O(nk), and the optimized heap is O(n+klogn), but with the fast queue distortion, you can handle all the problems in general (it's a bit difficult for the interviewer to sort your handwritten heaps).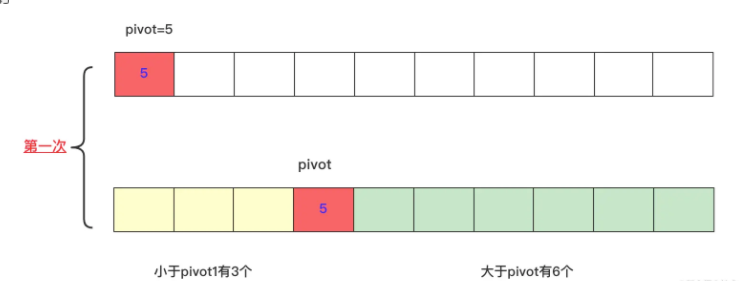

 

 

Quick Row determines the pivot position of a number each time, dividing the number into two parts: the left side is smaller than the pivot, and the right side is larger than the pivot, so that you can tell from this k whether it is exactly on the pivot position, or on the left or on the right side? You can compress the spatial iteration to invoke recursion to get the final result.

Many people reject this pivot as the first random choice (to fight tough test cases) in order to get faster than the test sample, but here I choose the first pivot for code reference:

class Solution {
    public int findKthLargest(int[] nums, int k) {
        quickSort(nums,0,nums.length-1,k);
        return nums[nums.length-k];
    }
    private void quickSort(int[] nums,int start,int end,int k) {
        if(start>end)
            return;
        int left=start;
        int right=end;
        int number=nums[start];
        while (left<right){
            while (number<=nums[right]&&left<right){
                right--;
            }
            nums[left]=nums[right];
            while (number>=nums[left]&&left<right){
                left++;
            }
            nums[right]=nums[left];
        }
        nums[left]=number;
        int num=end-left+1;
        if(num==k)//Terminate when k is found
            return;
        if(num>k){
            quickSort(nums,left+1,end,k);
        }else {
            quickSort(nums,start,left-1,k-num);
        }
    }
}

0X09 No Duplicate Longest Substring (Array)

This problem may be a string or an array, but it makes sense that the longest substring without duplicate characters is essentially the same as the longest array without duplicates.

The Title is: Given a string, find out the length of the longest substring that does not contain duplicate characters.

Analysis:

This question is to give a string to let you find the longest non-repeating substring. To clarify the differences between substrings and substrings:

Substring: Continuous, can be seen as part of the original string intercept. Subsequence: Not necessarily continuous, but keep the relative positions between elements constant.

So what do we do?

Violence search, violence search is certainly possible, but it is too complex to explain here. The idea selected here is a sliding window, a sliding window, that is, to use an interval from left to right, right to test first to find the maximum value of no repetition in the interval, and when there is repetition, move left to right until no repetition, then repeat until the end. Find the largest substring in the whole process.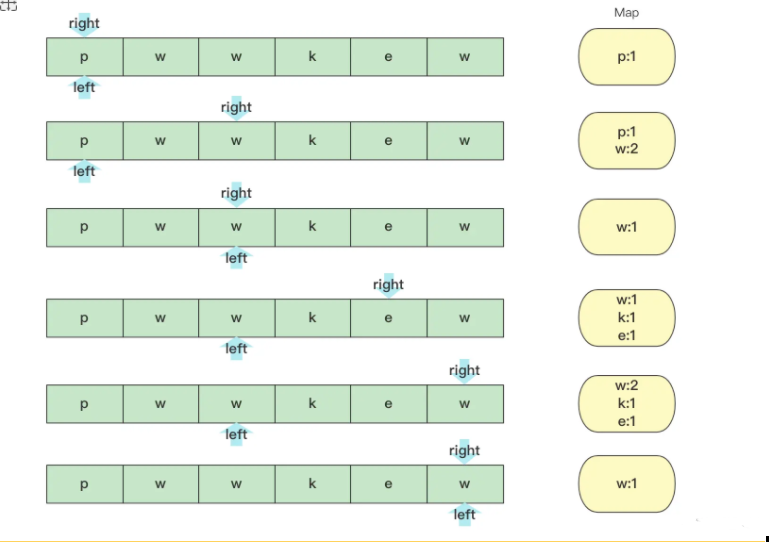

 

 

It is much faster to use arrays instead of hash tables for implementation:

class Solution {
    public int lengthOfLongestSubstring(String s) {
         int a[]=new int[128];
		 int max=0;//Maximum Records
		 int l=0;//left uses i as right and goes right when there are repetitions
		 for(int i=0;i<s.length();i++)
		 {
			 a[s.charAt(i)]++;
			 while (a[s.charAt(i)]>1) {
				a[s.charAt(l++)]--;
			}
			 if(i-l+1>max)
				 max=i-l+1;
		 }
		 return max;
    }
}

0X10 Sort

No one really thinks they're using Arrays.sort() is over. Handwritten sorting is still very frequent. Compared with simple people like bubble and insert, there are not many investigations such as heap sorting, Hill sorting, cardinality sorting, etc. Fast sorting is the most frequent one. There is an extra reward for merge sorting which is also very high frequency. Both are typical divide and conquer algorithms. Fast sorting can also be compared with the previous TOPK problem.

Top 10 sorting details have been described in detail, you can refer to: programmers will know the top 10 sorting

Quick Row: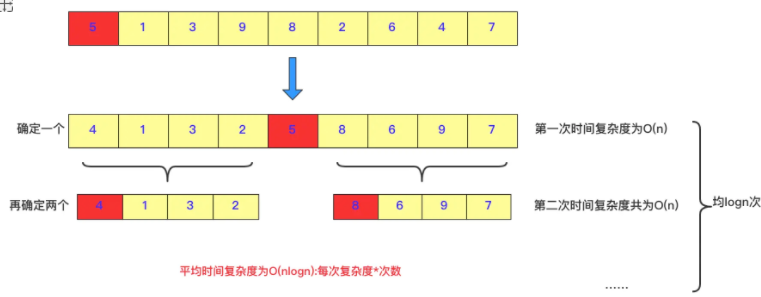

Specific implementation:

public void quicksort(int [] a,int left,int right)
{
  int low=left;
  int high=right;
  //The order of the following two sentences must not be confused, otherwise the array will be out of bounds!!! very important!!!
  if(low>high)//As a deadline for judging whether or not
    return;
  int k=a[low];//The extra space k, measured by the leftmost one, ends up requiring both the left side to be smaller and the right side to be larger than it.
  while(low<high)//This round requires that the left side be less than a[low] and the right side be greater than a[low].
  {
    while(low<high&&a[high]>=k)//The first stop less than k was found on the right
    {
      high--;
    }
    //So you'll find the first one smaller than it
    a[low]=a[high];//Place in low position
    while(low<high&&a[low]<=k)//Find the first one larger than k to the right of low and place it at the right a[high]
    {
      low++;
    }
    a[high]=a[low];			
  }
  a[low]=k;//Assign values and divide and conquer left and right recursively
  quicksort(a, left, low-1);
  quicksort(a, low+1, right);		
}

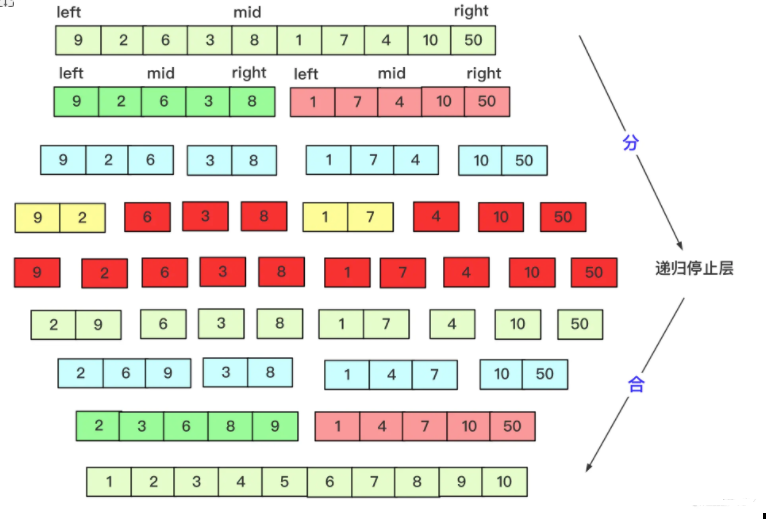
Merge Sort: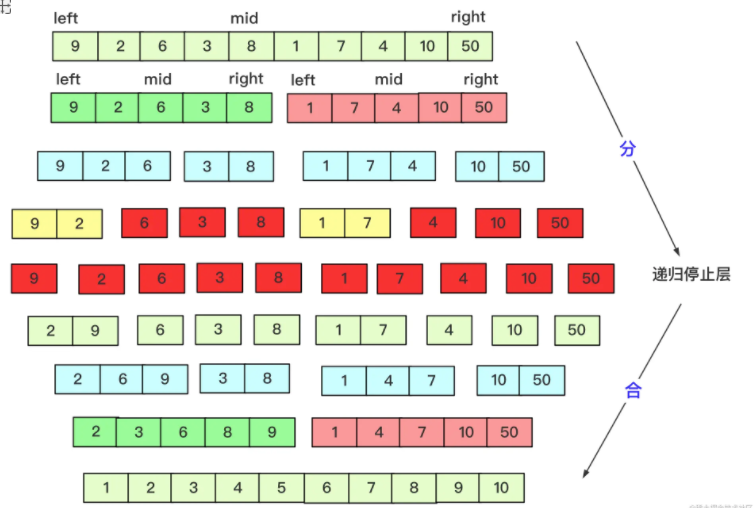

 

The implementation code is:

private static void mergesort(int[] array, int left, int right) {
  int mid=(left+right)/2;
  if(left<right)
  {
    mergesort(array, left, mid);
    mergesort(array, mid+1, right);
    merge(array, left,mid, right);
  }
}

private static void merge(int[] array, int l, int mid, int r) {
  int lindex=l;int rindex=mid+1;
  int team[]=new int[r-l+1];
  int teamindex=0;
  while (lindex<=mid&&rindex<=r) {//Compare Merge Left-Right First
    if(array[lindex]<=array[rindex])
    {
      team[teamindex++]=array[lindex++];
    }
    else {				
      team[teamindex++]=array[rindex++];
    }
  }
  while(lindex<=mid)//When a boundary is crossed, the rest can be added sequentially
  {
    team[teamindex++]=array[lindex++];

  }
  while(rindex<=r)
  {
    team[teamindex++]=array[rindex++];
  }	
  for(int i=0;i<teamindex;i++)
  {
    array[l+i]=team[i];
  }
}

epilogue

Okay, the 10 questions I'm sharing with you today are really very, very high frequency in interviews. I dare you have to meet one of them (no exaggeration) on average every two interviews!

Although the topic sea is very deep and incomplete, everyone who has learnt caching knows to cache hot spot data and those who have tried it knows to master the necessary points... These ten questions have been put to the mouth.