I introduction:
Mentioned before Custom Loss and metrics , the following is an inventory of the loss functions commonly used in Keras. Of course, they are also commonly used in daily production and development for future user-defined loss functions. Although there are many forms of loss function, it can never change without its origin. Loss functions abstract the objectives of random events such as regression, classification and other problems into non negative real numbers, so as to measure the loss or risk of the event, so as to correct the model and hope that the model will move towards the direction of minimum loss. However, here are only most cases, such as in some image combination algorithms, It will also maximize the loss and make the expression of the image more diversified and abstract.
II Common loss function
1. MAE mean absolute error
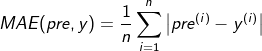
pre is the predicted value, y is the real value, and MAE is the sum of the absolute value of the difference between the predicted value and the real value
# Mean Ablsolutely Error
def getMaeLoss(predict, label):
loss = tf.reduce_mean(tf.losses.mean_absolute_error(label, predict))
return lossSimulate 100 samples for Loss calculation. If there is no special statement below, this sample will be used by default for Loss calculation.
numSamples = 100
predict = np.random.randint(0, 2, size=(numSamples,)).astype('float32')
label = np.random.randint(0, 2, size=(numSamples,)).astype('float32')
maeLoss = getMaeLoss(predict, label).numpy()
print("Mae Loss:", maeLoss)
2. MSE mean square error
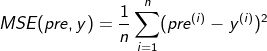
Pre is the predicted value, y is the real value, and MSE is the sum of the squares of the difference between the predicted value and the real value, which is the same as MAE. No matter whether pre is higher than y or lower than the same number, the calculated results are the same.
# Mean Squared Error
def getMseLoss(predict, label):
loss = tf.reduce_mean(tf.losses.mean_squared_error(label, predict))
return loss
3. RMSE root mean square error
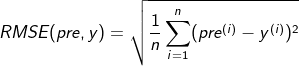
In fact, there is no difference between RMSE and MSE, but it is similar to the difference between variance and standard deviation. If the prediction target is 10000 yuan, the unit of MSE is 10000 * 10000, while RMSE is 10000. It is similar to a standardization process here.
# Root Mean Squared Error
def getRmseLoss(predict, label):
loss = tf.sqrt(tf.reduce_mean(tf.losses.mean_squared_error(label, predict)))
return loss
4. Mean_absolute_percentage_error
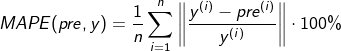
A MAPE of 0% indicates a perfect model, and a MAPE greater than 100% indicates a poor model. Note here that the denominator is 0.
# mean_absolute_percentage_error
def getMapeLoss(predict, label):
loss = tf.reduce_mean(tf.losses.mean_absolute_percentage_error(label, predict))
return loss
5. MSLE mean square logarithmic error
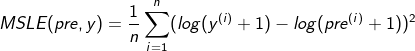
# Mean Squared Logarithmic Error (MSLE)
def getMsleLoss(predict, label):
loss = tf.reduce_mean(tf.losses.mean_squared_logarithmic_error(label, predict))
return loss(1) It can be seen that when the root mean square error is the same, the error in the case that the predicted value is smaller than the real value is relatively large, that is, the penalty for the case that the predicted value is small is relatively large.
(2) When there is a large difference between a small number of values in the data and the real value, the use of log function can reduce the impact of these values on the overall error.
y = np.array([2.,3.,4.,5.,6.])
predict = y + 2
print("The predicted value is greater than the real value:",getMsleLoss(predict, y))
predict = y - 2
print("The predicted value is less than the real value:",getMsleLoss(predict, y))The predicted value is greater than the real value: tf.Tensor(0.13689565089565417, shape=(), dtype=float64) The predicted value is less than the real value: tf.Tensor(0.44519201856286134, shape=(), dtype=float64)
6. Cosine Similarity
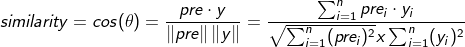
Cosine similarity generally considers the similarity of two vectors in space through the included angle, such as the common similarity calculation related to user embedding and item embedding.
# Cosine Loss
def getCosLoss(predict, label):
loss = tf.reduce_mean(tf.losses.cosine_similarity(label, predict))
return loss
7. Binary Crossentropy
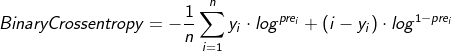
For binary classification, IMDB emotion analysis , gender prediction, etc.
# Binary Loss
def getBinaryLoss(predict, label):
loss = tf.reduce_mean(tf.losses.binary_crossentropy(label, predict))
return loss predict = utils.to_categorical(np.random.randint(0, 2, size=(numSamples,)).astype('int32'), num_classes=2)
label = utils.to_categorical(np.random.randint(0, 2, size=(numSamples,)).astype('int32'), num_classes=2)
binaryLoss = getBinaryLoss(predict, label).numpy()
print("Binary Loss: ", binaryLoss)
8. Category Crossentropy
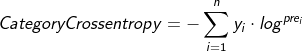
For multi category analysis, the most common Handwritten numeral recognition The cross entropy loss function is used, which is often used in combination with softmax function.
# Category Loss
def getCategoryLoss(predict, label):
loss = tf.reduce_mean(tf.losses.categorical_crossentropy(label, predict))
return loss predict = utils.to_categorical(np.random.randint(0, 10, size=(numSamples,)).astype('int32'), num_classes=10)
label = utils.to_categorical(np.random.randint(0, 10, size=(numSamples,)).astype('int32'), num_classes=10)
categoryLoss = getCategoryLoss(predict, label).numpy()
print("Category Loss: ", categoryLoss)
9. Kullback Leibler divergence KL divergence
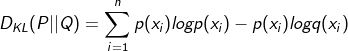
Here, information entropy is defined as:
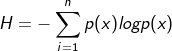
K-L divergence is used to measure the similarity of two steps in statistics. Here, P and Q can be regarded as the real value and predicted value.
# KL Loss
def getKLLoss(predict, label):
loss = tf.reduce_mean(tf.losses.kullback_leibler_divergence(label, predict))
return loss
10.Hinge Loss
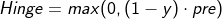
Hinge Loss is also called Hinge Loss, because its function image is very similar to the hinge of the door. The most common application scenario is SVM support vector machine.
# Hinge Loss
def getHingeLoss(predict, label):
loss = tf.reduce_mean(tf.losses.hinge(label, predict))
return loss predict = np.where(predict < 1, -1, 1).astype('float32')
label = np.where(label < 1, -1, 1).astype('float32')
hingeLoss = getHingeLoss(predict, label).numpy()
print("Hinge Loss: ", hingeLoss)
11. Poisson loss
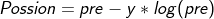
Referring to the official API, in order to prevent pre from being 0, it is later rewritten as y * log(pre + epsilon()), where epsilon() = 1e-07
# Possion Loss
def getPossionLoss(predict, label):
loss = tf.reduce_mean(tf.losses.poisson(label, predict))
return loss
12.Huber Loss smoothing mean absolute error
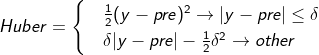
Huber smoothes the absolute error as its name implies. It is constructed as a piecewise function, which is between Mae and MSE. The degree of smoothing depends on δ When Huber loss is [0- δ, 0+ δ] In the interval, it is equivalent to MSE, while in [- ∞, δ] And[ δ,+ ∞] is MAE. Therefore, Huber is not sensitive to the square error of outliers in the data.
# Huber Loss
def getHuberLoss(predict, label):
loss = tf.reduce_mean(tf.losses.huber(label, predict))
return loss